วิธีสร้างแปลงตัวแปรต่อท้ายใน r

ในสถิติ แผนภาพตัวแปรที่เพิ่มเข้ามา คือแผนภาพแต่ละแผนภาพที่แสดงความสัมพันธ์ระหว่าง ตัวแปรตอบสนอง และตัวแปรทำนายในแบบจำลองการถดถอยเชิงเส้นพหุคูณ ในขณะที่ควบคุมการมีอยู่ของตัวแปรทำนายอื่นๆ ในแบบจำลอง

หมายเหตุ: บางครั้งแปลงเหล่านี้เรียกอีกอย่างว่า “แปลงการถดถอยบางส่วน”

พล็อตประเภทนี้ช่วยให้เราสามารถสังเกตความสัมพันธ์ระหว่างตัวแปรทำนายแต่ละตัวและตัวแปรตอบสนองในแบบจำลองในขณะที่คงตัวแปรทำนายอื่น ๆ ไว้คงที่

ในการสร้างแปลงของตัวแปรต่อท้ายใน R เราสามารถใช้ฟังก์ชัน avPlots() จากแพ็คเกจ car :

 #load car package
library (car) 

#fit multiple linear regression model
model <- lm(y ~ x1 + x2 + ..., data = df)

#create added variable plots
avPlots(model)

ตัวอย่างต่อไปนี้แสดงวิธีใช้ไวยากรณ์นี้ในทางปฏิบัติ

ตัวอย่าง: การเพิ่มแปลงตัวแปรใน R

สมมติว่าเราใส่โมเดลการถดถอยเชิงเส้นพหุคูณต่อไปนี้ใน R โดยใช้ข้อมูลจากชุดข้อมูล mtcars :

 #fit multiple linear regression model
model <- lm(mpg ~ disp + hp + drat, data = mtcars)

#view summary of model
summary(model)

Call:
lm(formula = mpg ~ disp + hp + drat, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-5.1225 -1.8454 -0.4456 1.1342 6.4958 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)   
(Intercept) 19.344293 6.370882 3.036 0.00513 **
available -0.019232 0.009371 -2.052 0.04960 * 
hp -0.031229 0.013345 -2.340 0.02663 * 
drat 2.714975 1.487366 1.825 0.07863 . 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.008 on 28 degrees of freedom
Multiple R-squared: 0.775, Adjusted R-squared: 0.7509 
F-statistic: 32.15 on 3 and 28 DF, p-value: 3.28e-09

เพื่อให้เห็นภาพความสัมพันธ์ระหว่างตัวแปรตอบสนอง “mpg” และตัวแปรทำนายแต่ละตัวในโมเดล เราสามารถสร้างพล็อตของตัวแปรที่เพิ่มเข้ามาได้โดยใช้ฟังก์ชัน avPlots()

 #load car package
library (car)

#produce added variable plots
avPlots(model)

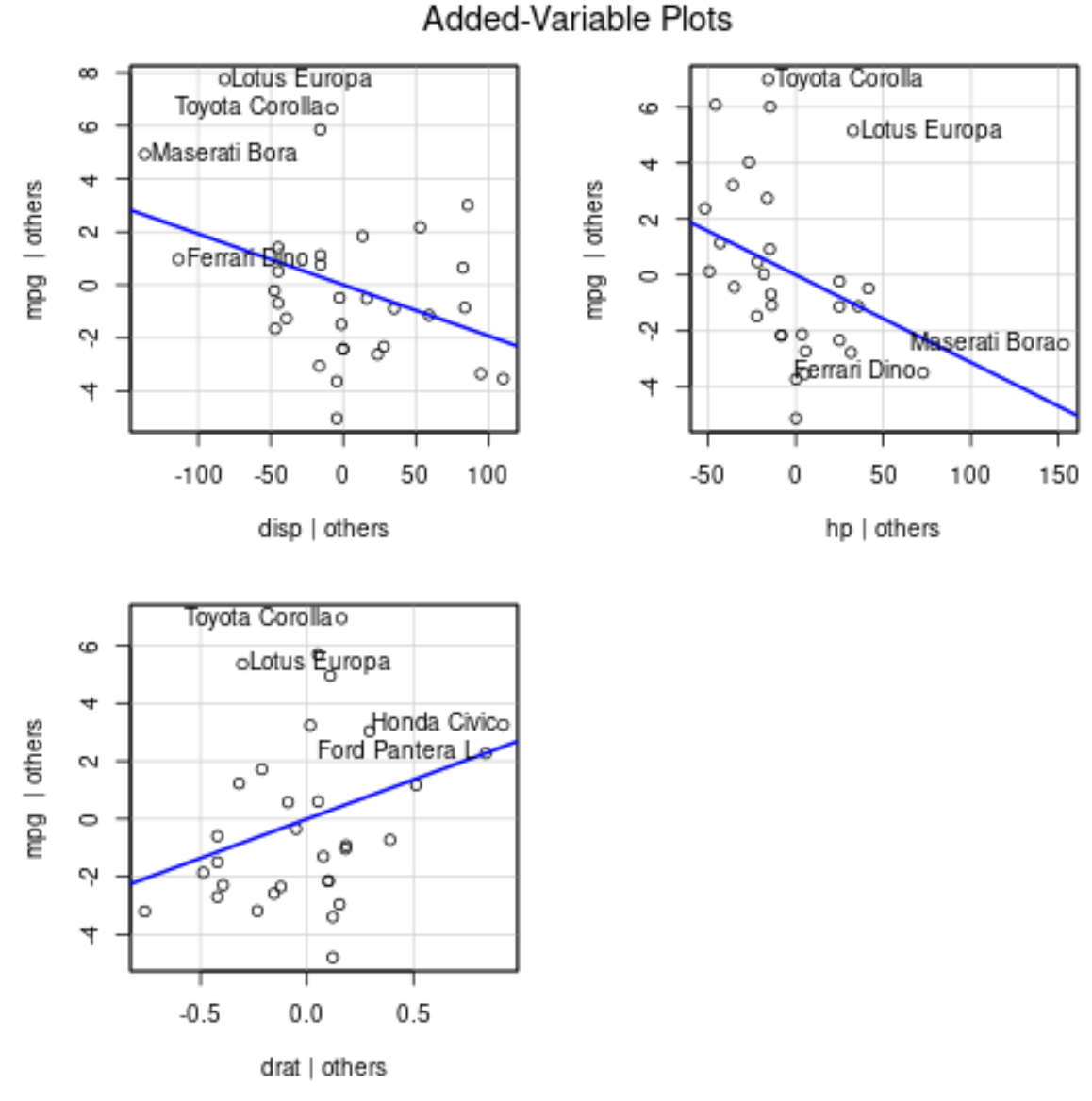
ต่อไปนี้เป็นวิธีตีความแต่ละพล็อต:

• แกน x จะแสดงตัวแปรทำนายเดี่ยว และแกน y จะแสดงตัวแปรการตอบสนอง
• เส้นสีน้ำเงินแสดงความสัมพันธ์ระหว่างตัวแปรทำนายและตัวแปรตอบสนอง ในขณะที่คงค่าของตัวแปรทำนายอื่นๆ ทั้งหมดไว้คงที่
• จุดที่ติดป้ายกำกับในแต่ละกราฟแสดงถึงการสังเกตสองครั้งที่มี ปริมาณคงเหลือ มากที่สุด และการสังเกตทั้งสองที่มีการงัดบางส่วนที่ใหญ่ที่สุด

โปรดทราบว่ามุมของเส้นในแต่ละโครงสอดคล้องกับเครื่องหมายของสัมประสิทธิ์ของสมการการถดถอยโดยประมาณ

ตัวอย่างเช่น ต่อไปนี้เป็นค่าสัมประสิทธิ์โดยประมาณสำหรับตัวแปรทำนายแต่ละตัวในแบบจำลอง:

• จอแสดงผล: -0.019232
• ช: -0.031229
• วันที่: 2.714975

โปรดทราบว่ามุมของเส้นเป็นบวกในพล็อตตัวแปรที่เพิ่มสำหรับ drat ในขณะที่มุมของเส้นเป็นลบสำหรับ disp และ hp ซึ่งสอดคล้องกับสัญญาณของสัมประสิทธิ์โดยประมาณ:

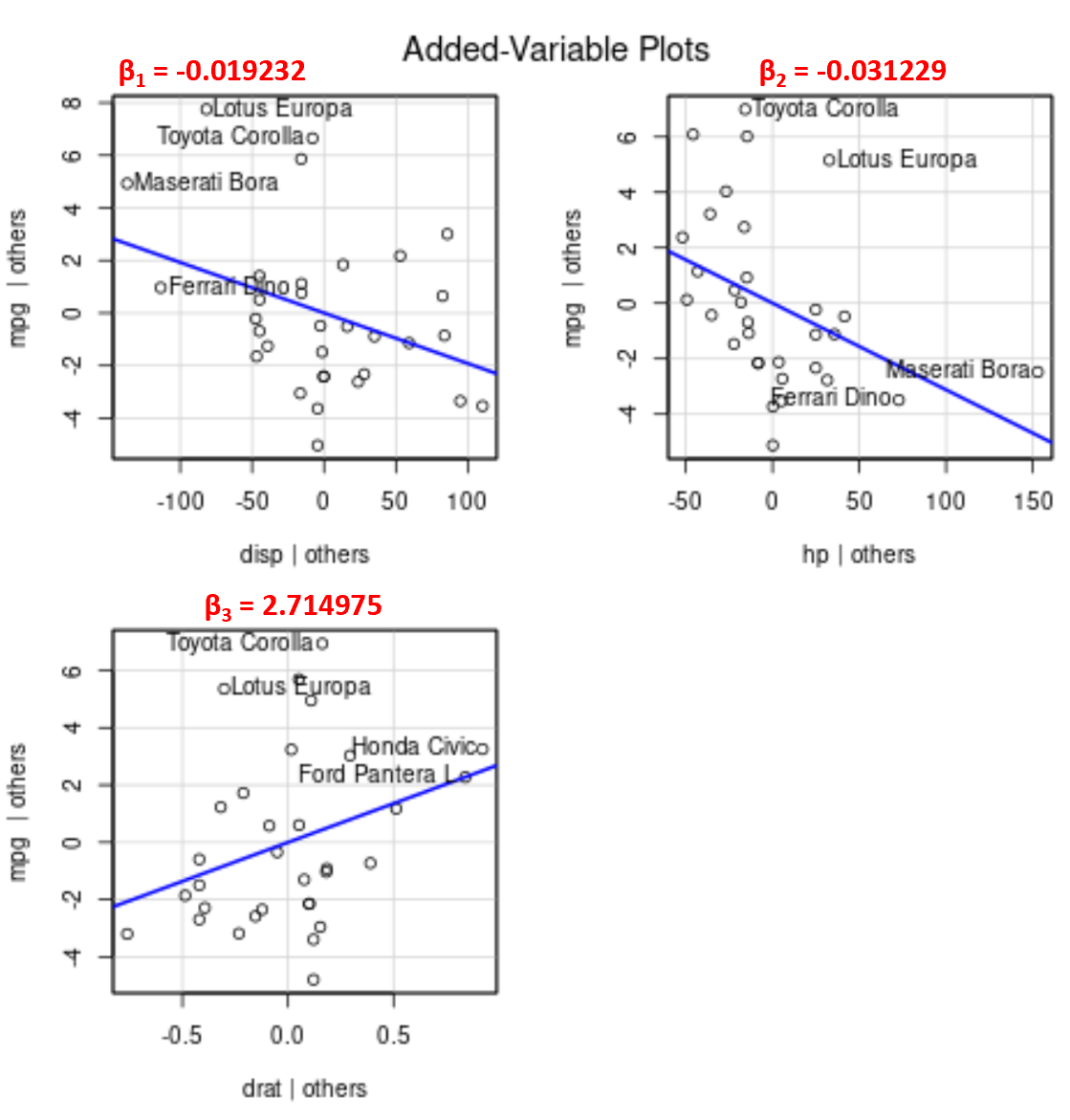
กราฟเหล่านี้ช่วยให้เราเห็นภาพความสัมพันธ์ระหว่างตัวแปรทำนายแต่ละตัวและตัวแปรตอบสนองได้อย่างง่ายดาย

แหล่งข้อมูลเพิ่มเติม

วิธีดำเนินการถดถอยเชิงเส้นอย่างง่ายใน R
วิธีดำเนินการถดถอยเชิงเส้นพหุคูณใน R
วิธีดำเนินการถดถอยโลจิสติกใน R