เมทริกซ์สหสัมพันธ์

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

ในบทความนี้ คุณจะค้นพบว่าเมทริกซ์สหสัมพันธ์คืออะไร สูตรของเมทริกซ์คืออะไร และวิธีตีความเมทริกซ์สหสัมพันธ์ นอกจากนี้ คุณจะสามารถดูตัวอย่างการตีความเมทริกซ์สหสัมพันธ์ที่เป็นรูปธรรมได้

เมทริกซ์สหสัมพันธ์คืออะไร?

เมทริกซ์สหสัมพันธ์คือเมทริกซ์ซึ่งมีตำแหน่ง i,j ค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร i และ j .

ดังนั้นเมทริกซ์สหสัมพันธ์จึงเป็นเมทริกซ์จตุรัสที่เต็มไปด้วยเมทริกซ์บนเส้นทแยงมุมหลักและองค์ประกอบของแถว i และคอลัมน์ j ประกอบด้วยค่าของสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปร i และตัวแปร j .

สูตรสำหรับเมทริกซ์สหสัมพันธ์ จึงเป็นดังนี้:

ทอง

$r_{ij}$

คือค่าสัมประสิทธิ์สหสัมพันธ์ระหว่างตัวแปรต่างๆ

$i$

และ

$j.$

ดังนั้น เพื่อที่จะค้นหาเมทริกซ์สหสัมพันธ์ของชุดข้อมูล จำเป็นอย่างยิ่งที่คุณจะต้องรู้วิธีคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ ในกรณีที่คุณจำไม่ได้ ในลิงค์ต่อไปนี้ คุณจะพบวิธีดำเนินการด้วยเครื่องคิดเลขออนไลน์:

➤ ดู: เครื่องคำนวณค่าสัมประสิทธิ์สหสัมพันธ์

คุณสมบัติของค่าสัมประสิทธิ์สหสัมพันธ์คือลำดับของตัวแปรไม่สำคัญสำหรับการคำนวณ กล่าวคือ ค่าสัมประสิทธิ์สหสัมพันธ์

$r_{ij}$

เทียบเท่ากับ

$r_{ji}.$

ดังนั้นเมทริกซ์สหสัมพันธ์จึงสมมาตร

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

เพื่อให้เมทริกซ์สหสัมพันธ์มีความหมาย ชุดข้อมูลทางสถิติต้องมีตัวแปรมากกว่าสองตัว มิฉะนั้น ก็จะเพียงพอที่จะกำหนดค่าสัมประสิทธิ์สหสัมพันธ์เพียงค่าเดียวและเมทริกซ์สหสัมพันธ์จะมีความหมาย

วิธีสร้างเมทริกซ์สหสัมพันธ์

เมื่อพิจารณาถึงคำจำกัดความของเมทริกซ์สหสัมพันธ์ เรามาดูกันว่าเมทริกซ์ทางสถิติประเภทนี้ถูกสร้างขึ้นอย่างไร:

คำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของตัวแปรแต่ละคู่ โปรดทราบว่าลำดับของตัวแปรจะไม่เปลี่ยนแปลงผลลัพธ์ ดังนั้นจึงต้องคำนวณเพียงครั้งเดียวสำหรับตัวแปรแต่ละคู่
สร้างเมทริกซ์จตุรัสที่มีมิติเดียวกันกับจำนวนตัวแปรในชุดข้อมูล เมทริกซ์นี้จะเป็นเมทริกซ์สหสัมพันธ์
ใส่ 1 ในแต่ละองค์ประกอบของเส้นทแยงมุมหลักของเมทริกซ์สหสัมพันธ์
ใส่สัมประสิทธิ์สหสัมพันธ์ของตัวแปร i , j ในตำแหน่ง i , j และ j , i
เมื่อเมทริกซ์สหสัมพันธ์ถูกสร้างขึ้น สิ่งที่เหลืออยู่คือการตีความค่าของมัน

โปรดจำไว้ว่าการเรียกใช้เมทริกซ์สหสัมพันธ์นั้นไม่เพียงพอ คุณต้องตีความค่าของมันและทำความเข้าใจว่ามันหมายถึงอะไร ส่วนต่อไปนี้จะอธิบายวิธีการตีความเมทริกซ์สหสัมพันธ์

การตีความเมทริกซ์สหสัมพันธ์

ในการตีความเมทริกซ์สหสัมพันธ์อย่างถูกต้อง จำเป็นต้องคำนึงว่าค่าของสัมประสิทธิ์สหสัมพันธ์สามารถอยู่ในช่วงตั้งแต่ -1 ถึง +1:

r=-1 : ตัวแปรทั้งสองมีความสัมพันธ์เชิงลบที่สมบูรณ์แบบ ดังนั้นเราจึงสามารถวาดเส้นที่มีความชันเป็นลบโดยที่จุดทั้งหมดเชื่อมโยงกัน
-1<r<0 : ความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นเป็นลบ ดังนั้นเมื่อตัวแปรตัวหนึ่งเพิ่มขึ้น อีกตัวแปรหนึ่งก็จะลดลง ยิ่งค่าเข้าใกล้ -1 มากเท่าใด ตัวแปรก็จะยิ่งมีความสัมพันธ์เชิงลบมากขึ้นเท่านั้น
r=0 : ความสัมพันธ์ระหว่างตัวแปรทั้งสองนั้นอ่อนแอมาก จริงๆ แล้วความสัมพันธ์เชิงเส้นระหว่างตัวแปรทั้งสองนั้นเป็นศูนย์ นี่ไม่ได้หมายความว่าตัวแปรมีความเป็นอิสระ เนื่องจากอาจมีความสัมพันธ์แบบไม่เชิงเส้นได้
0<r<1 : ความสัมพันธ์ระหว่างตัวแปรทั้งสองเป็นค่าบวก ยิ่งค่าเข้าใกล้ +1 มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น ในกรณีนี้ ตัวแปรตัวหนึ่งมีแนวโน้มที่จะเพิ่มมูลค่าเมื่ออีกตัวแปรหนึ่งเพิ่มขึ้นเช่นกัน
r=1 : ตัวแปรทั้งสองมีความสัมพันธ์เชิงบวกที่สมบูรณ์แบบ กล่าวคือ ตัวแปรทั้งสองมีความสัมพันธ์เชิงเส้นเชิงบวก

ดังนั้น ในการตีความเมทริกซ์สหสัมพันธ์ จึงจำเป็นต้องตีความค่าสัมประสิทธิ์สหสัมพันธ์แต่ละรายการและเปรียบเทียบผลลัพธ์ที่ต่างกัน

ด้วยวิธีนี้ คุณจะสามารถดูได้ว่าตัวแปรใดมีความเกี่ยวข้องกันมากที่สุด ตัวแปรใดที่สำคัญที่สุด ตัวแปรใดแทบไม่มีความสัมพันธ์กันเลย เป็นต้น

ตัวอย่างเมทริกซ์สหสัมพันธ์

เพื่อให้เข้าใจอย่างถ่องแท้ว่าเมทริกซ์สหสัมพันธ์ประกอบด้วยอะไรและตีความอย่างไร ในส่วนนี้ เราจะวิเคราะห์ตัวอย่างของเมทริกซ์สหสัมพันธ์:

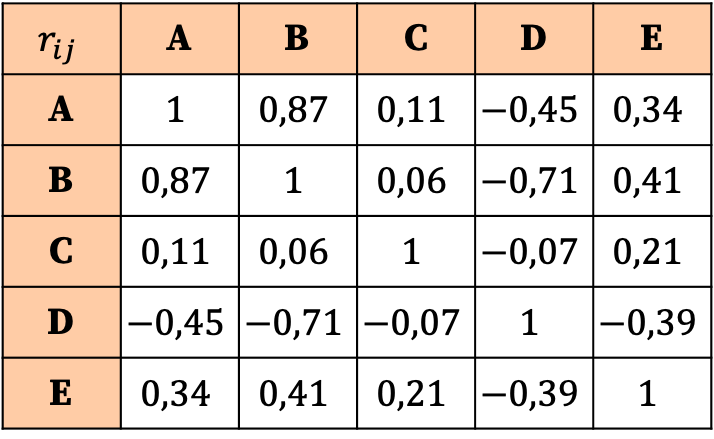
การตีความเมทริกซ์สหสัมพันธ์นั้นขึ้นอยู่กับค่าของสัมประสิทธิ์ ดังนั้น เราจะเห็นได้ว่าความสัมพันธ์ที่แข็งแกร่งที่สุดคือความสัมพันธ์ระหว่างตัวแปร A และตัวแปร B เนื่องจากค่าสัมประสิทธิ์ที่สอดคล้องกันนั้นมีค่ามากที่สุด (0.87)

ในทางกลับกัน ตัวแปร C ไม่มีความสัมพันธ์กับตัวแปรใดๆ เลย เนื่องจากค่าสัมประสิทธิ์ทั้งหมดใกล้กับศูนย์มากและจึงต่ำมาก ดังนั้น เพื่อให้การวิเคราะห์ง่ายขึ้น เราอาจพิจารณาลบตัวแปรนี้ออกจากการศึกษาทางสถิติด้วยซ้ำ

ในทำนองเดียวกัน ความสัมพันธ์ทั้งหมดของตัวแปร D กับตัวแปรอื่นๆ จะเป็นลบ ซึ่งหมายความว่าความสัมพันธ์ระหว่างตัวแปร D กับตัวแปรอื่นๆ จะเป็นค่าผกผัน นี่ไม่ได้หมายความว่าควรกำจัดตัวแปร เพียงแต่ว่าตัวแปร D มีความสัมพันธ์เชิงลบเท่านั้น

อย่างที่คุณเห็นเมทริกซ์สหสัมพันธ์มีประโยชน์มากสำหรับการสรุปข้อมูลและทำการวิเคราะห์โดยรวมของความสัมพันธ์ระหว่างตัวแปรต่างๆ ในชุดข้อมูล

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม