วิธีสร้างเมทริกซ์สหสัมพันธ์ใน spss
เมทริกซ์สหสัมพันธ์ คือตารางสี่เหลี่ยมที่แสดงค่าสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สันระหว่างตัวแปรต่างๆ ในชุดข้อมูล
ขอย้ำเตือนว่า สัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน เป็นหน่วยวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสอง ตัว ใช้ค่าระหว่าง -1 ถึง 1 โดยที่:
- -1 บ่งชี้ถึงความสัมพันธ์เชิงเส้นเชิงลบอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
- 0 บ่งชี้ว่าไม่มีความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว
- 1 บ่งชี้ความสัมพันธ์เชิงเส้นเชิงบวกอย่างสมบูรณ์ระหว่างตัวแปรสองตัว
ยิ่งค่าสัมประสิทธิ์สหสัมพันธ์จากศูนย์มากเท่าใด ความสัมพันธ์ระหว่างตัวแปรทั้งสองก็จะยิ่งแข็งแกร่งขึ้นเท่านั้น
บทช่วยสอนนี้จะอธิบายวิธีสร้างและตีความเมทริกซ์สหสัมพันธ์ใน SPSS
ตัวอย่าง: วิธีการสร้างเมทริกซ์สหสัมพันธ์ใน SPSS
ทำตามขั้นตอนต่อไปนี้เพื่อสร้างเมทริกซ์สหสัมพันธ์สำหรับชุดข้อมูลนี้ซึ่งแสดงค่าเฉลี่ยแอสซิสต์ รีบาวด์ และแต้มของผู้เล่นบาสเก็ตบอล 8 คน:
ขั้นตอนที่ 1: เลือกความสัมพันธ์แบบไบวาเรียต
- คลิกแท็บ วิเคราะห์
- คลิก สัมพันธ์กัน
- คลิก ไบวาเรียต
ขั้นตอนที่ 2: สร้างเมทริกซ์สหสัมพันธ์
ตัวแปรแต่ละตัวในชุดข้อมูลจะเริ่มแสดงในช่องด้านซ้าย:
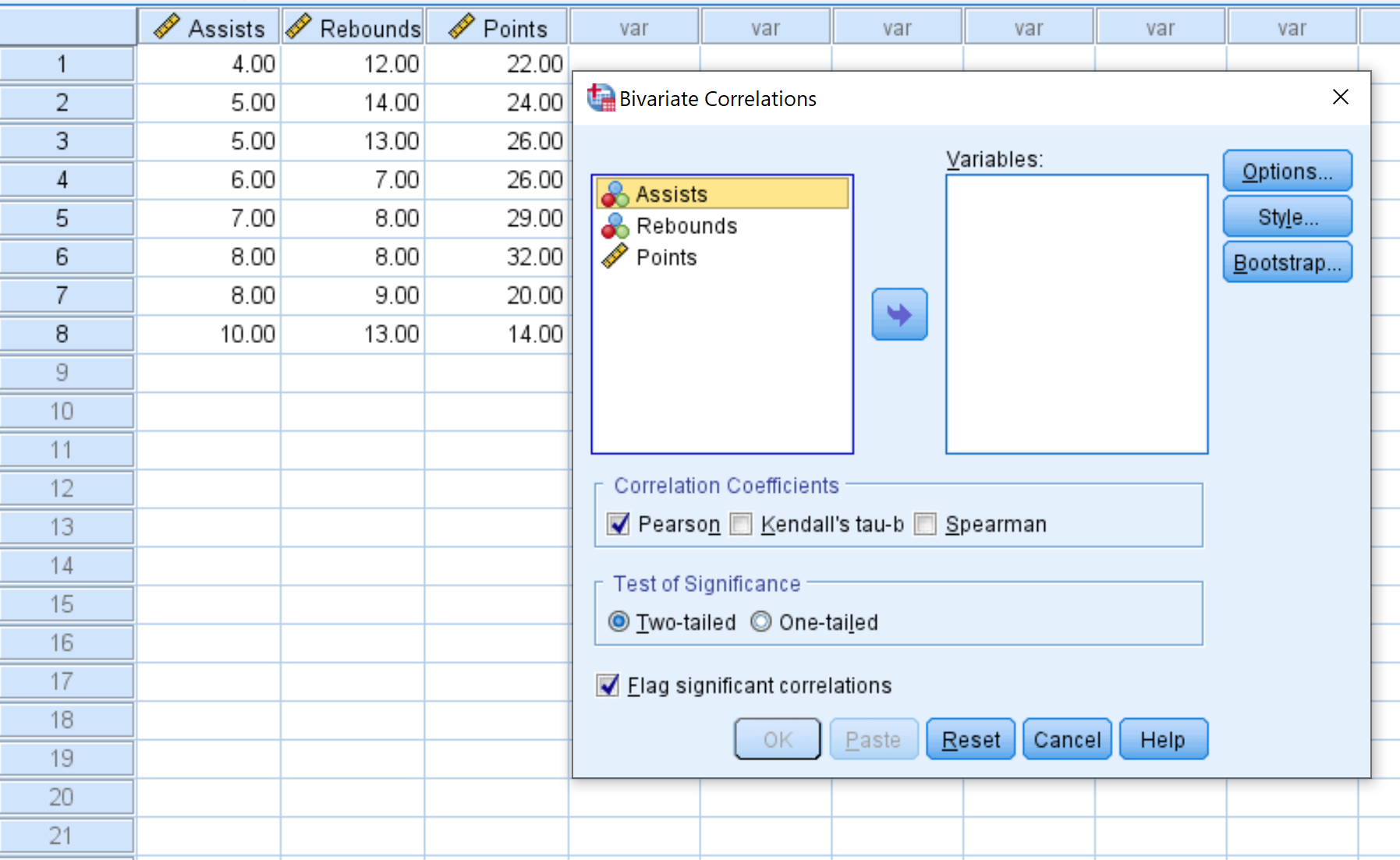
- เลือกตัวแปรแต่ละตัวที่คุณต้องการรวมไว้ในเมทริกซ์สหสัมพันธ์แล้วคลิกลูกศรเพื่อถ่ายโอนไปยังกล่อง ตัวแปร เราจะใช้ตัวแปรทั้งสามในตัวอย่างนี้
- ภายใต้ ค่าสัมประสิทธิ์สหสัมพันธ์ ให้เลือกว่าคุณต้องการใช้ความสัมพันธ์ของเพียร์สัน เอกภาพของเคนดัลล์ หรือความสัมพันธ์ของสเปียร์แมน เราจะปล่อยให้มันเป็นเพียร์สันสำหรับตัวอย่างนี้
- ภายใต้ การทดสอบนัยสำคัญ ให้เลือกว่าคุณต้องการใช้การทดสอบแบบสองด้านหรือแบบด้านเดียวเพื่อพิจารณาว่าตัวแปรสองตัวมีความสัมพันธ์กันที่มีนัยสำคัญทางสถิติหรือไม่ เราจะปล่อยให้มันเป็นสองด้าน
- ทำเครื่องหมายที่ช่องถัดจาก รายงานความสัมพันธ์ที่มีนัยสำคัญ หากคุณต้องการให้ SPSS รายงานตัวแปรที่มีความสัมพันธ์กันอย่างมีนัยสำคัญ
- สุดท้ายคลิก ตกลง
เมื่อคุณคลิก ตกลง เมทริกซ์สหสัมพันธ์ต่อไปนี้จะปรากฏขึ้น:
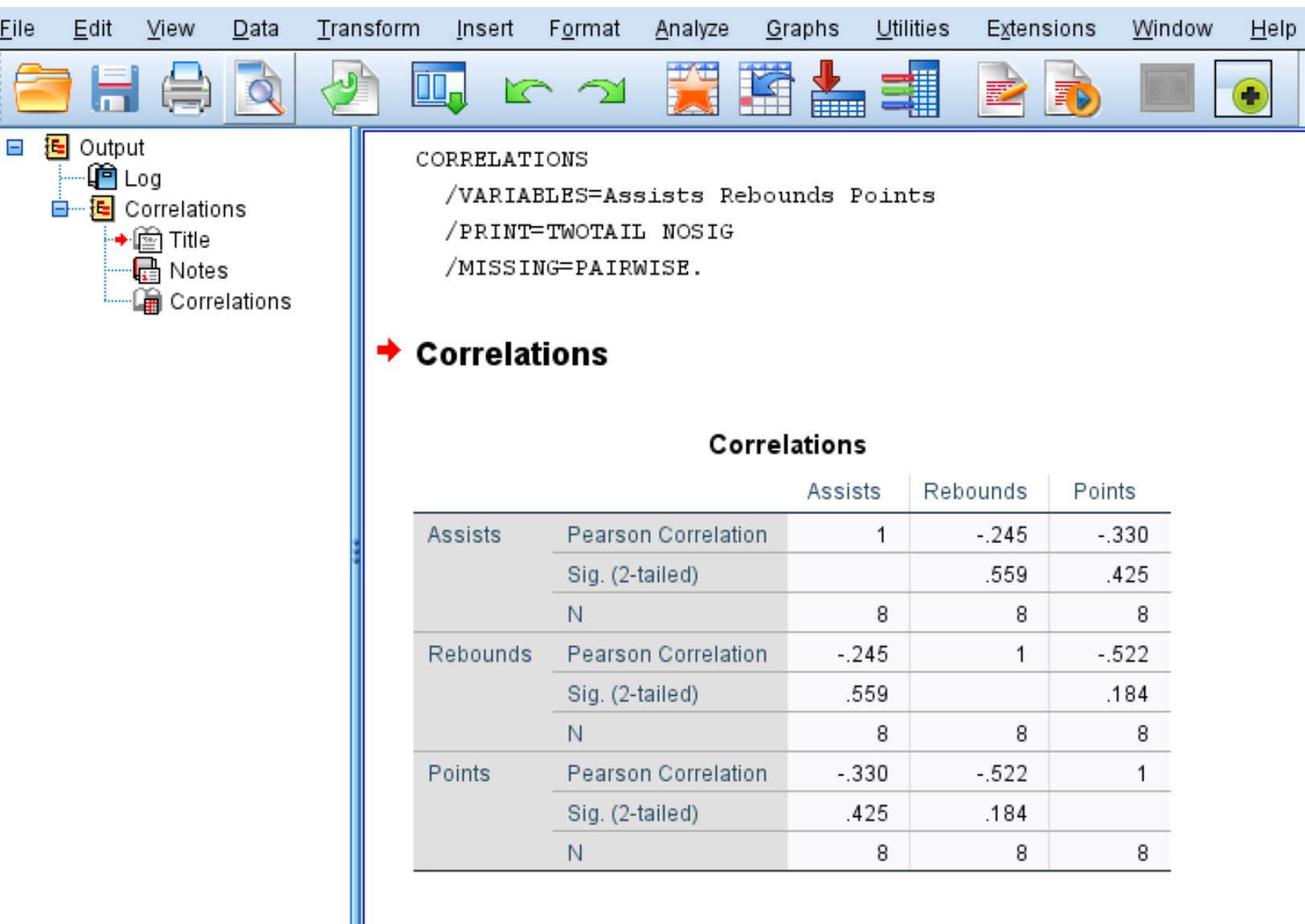
ขั้นตอนที่ 3: ตีความเมทริกซ์สหสัมพันธ์
เมทริกซ์สหสัมพันธ์จะแสดงการวัดสามค่าต่อไปนี้สำหรับแต่ละตัวแปร:
- ความสัมพันธ์แบบเพียร์สัน: การวัดความสัมพันธ์เชิงเส้นระหว่างตัวแปรสองตัว ตั้งแต่ -1 ถึง 1
- ซิก (สองด้าน): ค่า p สองด้านที่เกี่ยวข้องกับสัมประสิทธิ์สหสัมพันธ์ ซึ่งจะบอกคุณว่าตัวแปรสองตัวมีความสัมพันธ์กันที่มีนัยสำคัญทางสถิติหรือไม่ (เช่น ถ้า p < 0.05)
- N: จำนวนคู่ที่ใช้ในการคำนวณสัมประสิทธิ์สหสัมพันธ์แบบเพียร์สัน
ตัวอย่างเช่น ต่อไปนี้เป็นวิธีการตีความผลลัพธ์ของตัวแปร Assists:
- ค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันระหว่างแอสซิสต์และการรีบาวด์คือ -0.245 เนื่องจากจำนวนนี้เป็นลบ หมายความว่าตัวแปรทั้งสองมีความสัมพันธ์กันเป็นลบ
- ค่า p ที่เกี่ยวข้องกับสัมประสิทธิ์สหสัมพันธ์เพียร์สันสำหรับการแอสซิสต์และการรีบาวด์คือ 0.559 เนื่องจากค่านี้ไม่น้อยกว่า 0.05 ตัวแปรทั้งสองจึงไม่มีความเชื่อมโยงที่มีนัยสำคัญทางสถิติ
- จำนวนคู่ที่ใช้ในการคำนวณค่าสัมประสิทธิ์สหสัมพันธ์ของเพียร์สันคือ 8 (เช่น ใช้ผู้เล่น 8 คู่ในการคำนวณนี้)
ขั้นตอนที่ 4: แสดงภาพเมทริกซ์สหสัมพันธ์
คุณยังสามารถสร้างเมทริกซ์การลงจุดกระจายเพื่อให้เห็นภาพความสัมพันธ์เชิงเส้นระหว่างตัวแปรแต่ละตัวได้
- คลิกแท็บ แผนภูมิ
- คลิก ตัวสร้างแผนภูมิ
- สำหรับประเภทแผนภูมิ คลิก กระจาย/จุด
- คลิกที่ภาพที่ระบุว่า Scatterplot Matrix
- ในกล่อง ตัวแปร ที่ด้านซ้ายบน ให้กด Ctrl ค้างไว้แล้วคลิกชื่อตัวแปรทั้งสาม ลากไปยังกล่องที่ด้านล่างของแผนภูมิที่ระบุว่า Scattermatrix
- สุดท้ายคลิก ตกลง
เมทริกซ์ Scatterplot ต่อไปนี้จะปรากฏขึ้นโดยอัตโนมัติ:
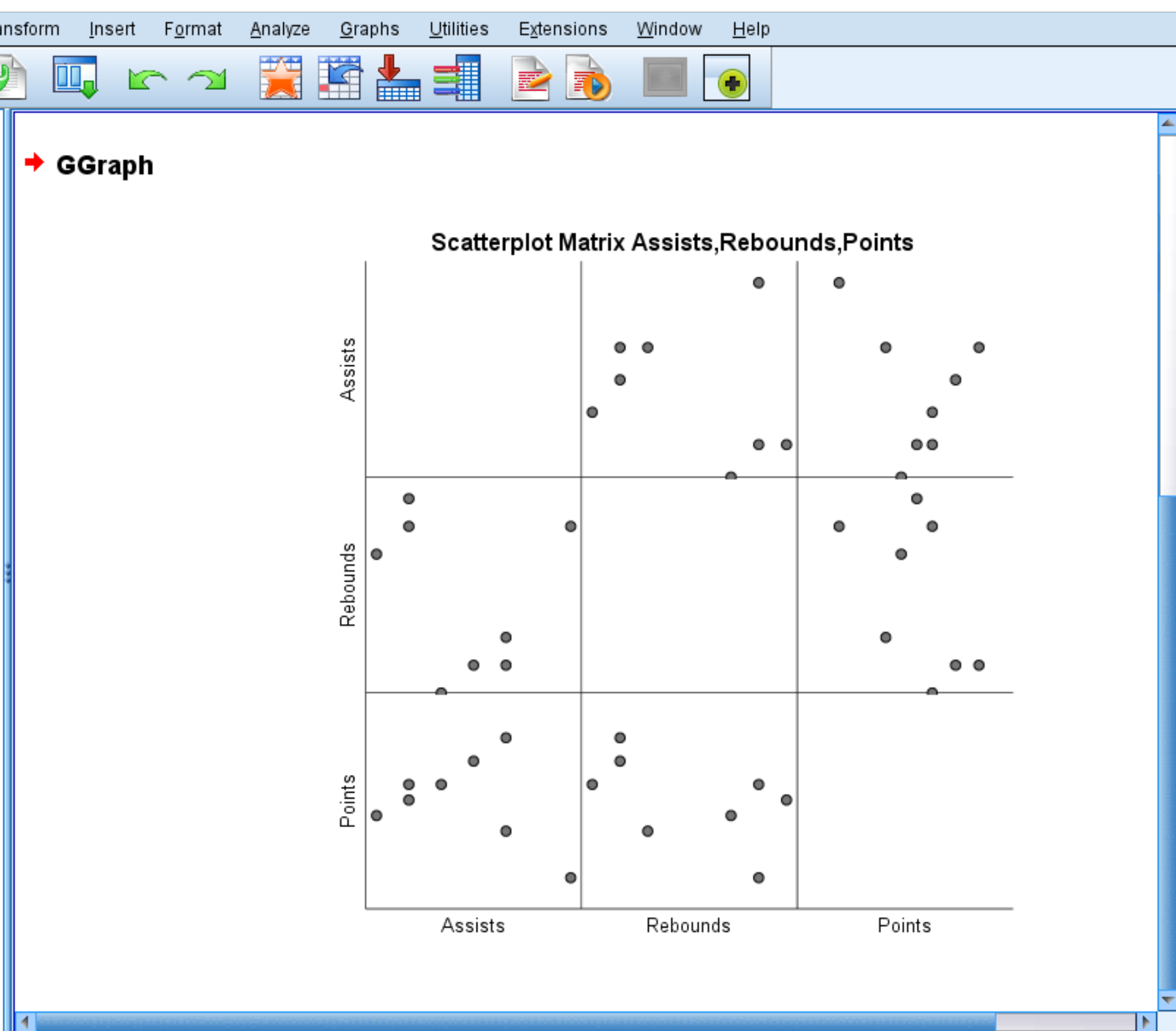
แผนภูมิกระจายแต่ละรายการจะแสดงการรวมกันแบบคู่ระหว่างตัวแปรสองตัว ตัวอย่างเช่น แผนภูมิกระจายที่มุมซ้ายล่างจะแสดงการรวมกันของคะแนนและการช่วยเหลือสำหรับผู้เล่น 8 คนแต่ละคนในชุดข้อมูล
เมทริกซ์ Scatterplot เป็นทางเลือก แต่เป็นวิธีที่ดีในการแสดงภาพความสัมพันธ์ระหว่างการรวมตัวแปรแต่ละคู่ในชุดข้อมูล