Splines การถดถอยแบบอะแดปทีฟหลายตัวแปรใน r

สามารถใช้ เส้นโค้งการถดถอยแบบปรับตัวหลายตัวแปร (MARS) เพื่อสร้างแบบจำลองความสัมพันธ์แบบไม่เชิงเส้นระหว่างชุดตัวแปรทำนายและ ตัวแปรตอบสนอง

วิธีนี้ใช้ได้ผลดังนี้:

1. แบ่งชุดข้อมูลออกเป็น k ชิ้น

2. ติดตั้งแบบจำลองการถดถอยกับแต่ละส่วน

3. ใช้การตรวจสอบความถูกต้องแบบข้าม k-fold เพื่อเลือกค่าสำหรับ k

บทช่วยสอนนี้ให้ตัวอย่างทีละขั้นตอนของวิธีปรับแบบจำลอง MARS ให้พอดีกับชุดข้อมูลใน R

ขั้นตอนที่ 1: โหลดแพ็คเกจที่จำเป็น

สำหรับตัวอย่างนี้ เราจะใช้ชุด ข้อมูล ISLR Wage   แพ็คเกจซึ่งประกอบด้วยเงินเดือนประจำปีจำนวน 3,000 คน พร้อมด้วยตัวแปรทำนายที่หลากหลาย เช่น อายุ การศึกษา เชื้อชาติ และอื่นๆ

ก่อนที่จะปรับโมเดล MARS เข้ากับข้อมูล เราจะโหลดแพ็คเกจที่จำเป็น:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

ขั้นตอนที่ 2: ดูข้อมูล

ต่อไป เราจะแสดงหกแถวแรกของชุดข้อมูลที่เราใช้งานอยู่:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

ขั้นตอนที่ 3: สร้างและเพิ่มประสิทธิภาพโมเดล MARS

ต่อไป เราจะสร้างโมเดล MARS สำหรับชุดข้อมูลนี้ และดำเนิน การตรวจสอบข้าม k-fold เพื่อพิจารณาว่าโมเดลใดที่สร้างการทดสอบ RMSE ที่ต่ำที่สุด (ค่าคลาดเคลื่อนกำลังสองเฉลี่ย)

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

จากผลลัพธ์ เราจะเห็นว่าแบบจำลองที่สร้างการทดสอบ MSE ต่ำสุดนั้นเป็นแบบจำลองที่มีเอฟเฟกต์ลำดับที่หนึ่งเท่านั้น (เช่น ไม่มีเงื่อนไขการโต้ตอบ) และมี 12 เงื่อนไข แบบจำลองนี้สร้างข้อผิดพลาดกำลังสองเฉลี่ยรูต (RMSE) เท่ากับ 33.8164

หมายเหตุ: เราใช้ method=”earth” เพื่อระบุแบบจำลอง MARS คุณสามารถค้นหาเอกสารสำหรับวิธีนี้ ได้ที่นี่

นอกจากนี้เรายังสามารถสร้างแผนภูมิเพื่อแสดงภาพการทดสอบ RMSE ตามระดับและจำนวนเทอม:

 #display test RMSE by terms and degree
ggplot(cv_mars)

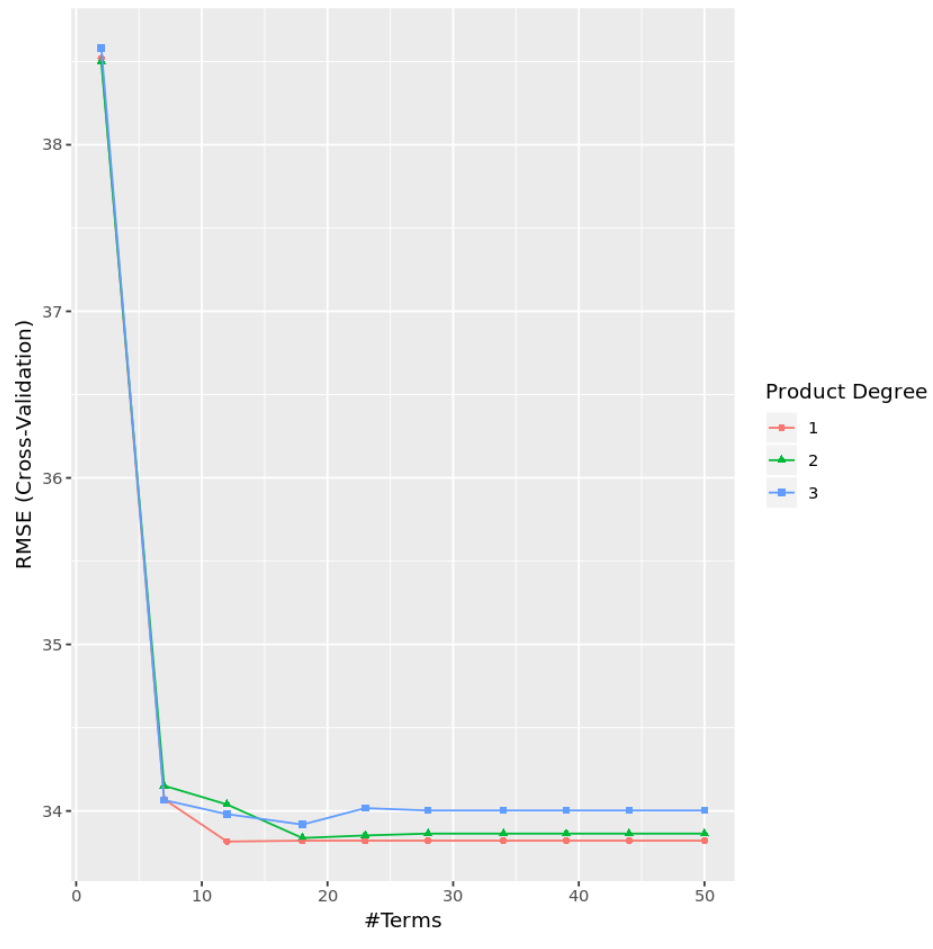
ในทางปฏิบัติ เราจะปรับโมเดล MARS เข้ากับโมเดลประเภทอื่นๆ หลายประเภท เช่น:

• การถดถอยเชิงเส้นพหุคูณ
• การถดถอยพหุนาม
• การถดถอยสูงสุด
• การถดถอยแบบ Lasso
• การถดถอยองค์ประกอบหลัก
• กำลังสองน้อยที่สุดบางส่วน

จากนั้นเราจะเปรียบเทียบแต่ละรุ่นเพื่อดูว่ารุ่นใดทำให้เกิดข้อผิดพลาดในการทดสอบต่ำที่สุด และเลือกรุ่นนั้นเป็นรุ่นที่เหมาะสมที่สุดที่จะใช้

สามารถดูโค้ด R แบบเต็มที่ใช้ในตัวอย่างนี้ ได้ ที่นี่