เส้นโค้งความหนาแน่นคืออะไร? (คำอธิบายและตัวอย่าง)

เส้นโค้งความหนาแน่น คือเส้นโค้งบนกราฟที่แสดงการกระจายของค่าในชุดข้อมูล สิ่งนี้มีประโยชน์ด้วยเหตุผลสามประการ:

1. เส้นโค้งความหนาแน่นทำให้เรามีความคิดที่ดีเกี่ยวกับ “รูปร่าง” ของการแจกแจง รวมถึงการแจกแจงที่มีค่าความถี่ “พีค” อย่างน้อยหนึ่งค่าหรือไม่ และการกระจายนั้นเบ้ไปทางซ้ายหรือไม่ หรือถูก. ขวา. .

2. เส้นโค้งความหนาแน่นช่วยให้เรามองเห็นได้ว่า ค่าเฉลี่ยและค่ามัธยฐาน ของการแจกแจงสัมพันธ์กันอย่างไร

3. เส้นโค้งความหนาแน่นช่วยให้เรามองเห็นเปอร์เซ็นต์ของการสังเกตในชุดข้อมูลที่อยู่ระหว่างค่าที่ต่างกัน

เส้นโค้งความหนาแน่นที่รู้จักกันดีที่สุดคือเส้นโค้งรูประฆังซึ่งแสดงถึง การกระจายตัวแบบปกติ

เพื่อให้เข้าใจเส้นโค้งความหนาแน่นได้ดีขึ้น ลองพิจารณาตัวอย่างต่อไปนี้

ตัวอย่าง: การสร้างและการตีความเส้นโค้งความหนาแน่น

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่แสดงความสูงของต้นที่แตกต่างกัน 20 ต้น (เป็นนิ้ว) ในบางฟิลด์:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

หากเราสร้างฮิสโตแกรมอย่างง่ายเพื่อแสดงความถี่สัมพัทธ์ของแต่ละค่า มันจะมีลักษณะดังนี้:

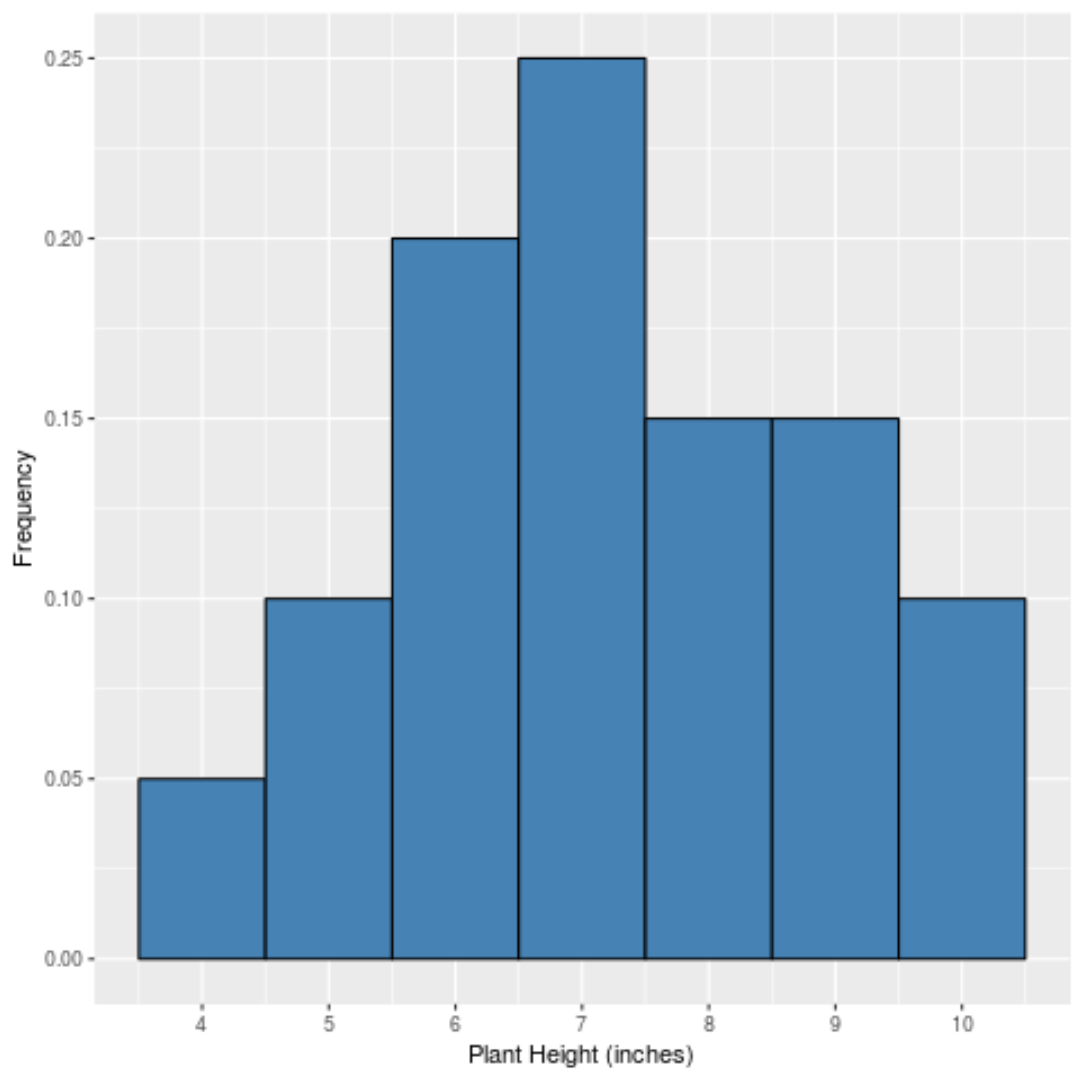
แกน x แสดงค่าข้อมูล และแกน y แสดงความถี่สัมพัทธ์ (เช่น ค่า “7” ปรากฏ 5 ครั้งจากทั้งหมด 20 ค่าในชุดข้อมูล จึงมีความถี่สัมพัทธ์ 25% หรือ 0.25 .

และถ้าเราสร้าง เส้นโค้งความหนาแน่น เพื่อจับ “รูปร่าง” ของการกระจายตัวนี้ มันจะมีลักษณะดังนี้:

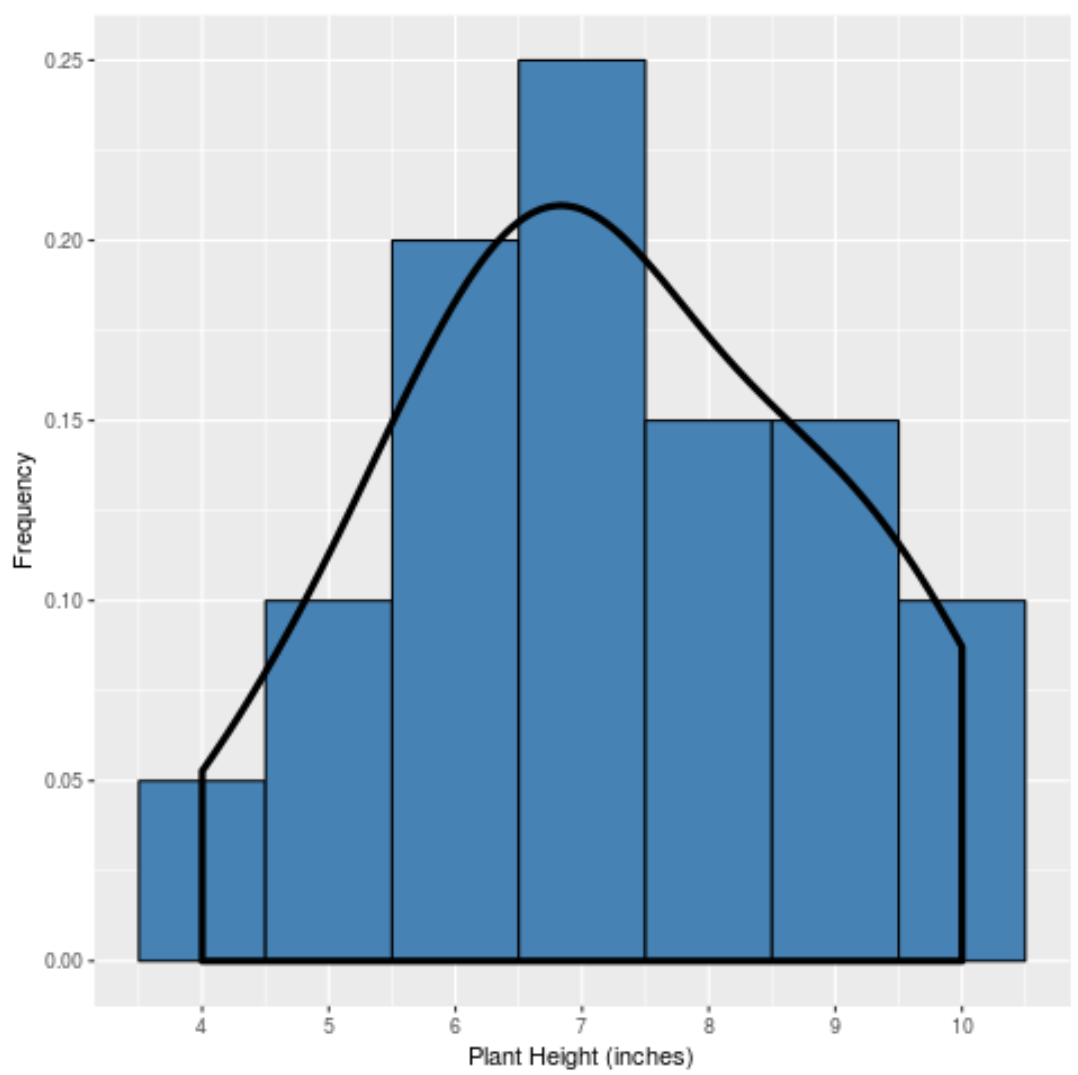
เส้นโค้งจะอยู่สูงที่สุดใกล้กับศูนย์กลางของการแจกแจงเพราะนั่นคือจุดที่พบค่าส่วนใหญ่ นอกจากนี้ยังต่ำที่สุดเมื่อใกล้ถึงจุดสิ้นสุดของการกระจายเนื่องจากมีพืชน้อยกว่าที่ใช้ค่าเหล่านี้ (เช่น ความสูง 4 นิ้วหรือ 10 นิ้ว)

วิธีการตีความเส้นโค้งความหนาแน่น

เส้นโค้งความหนาแน่นมาในรูปทรงและขนาดต่างๆ และช่วยให้เราเข้าใจการกระจายของค่าในชุดข้อมูลที่กำหนดได้อย่างรวดเร็ว มีประโยชน์อย่างยิ่งในการช่วยให้เราเห็นภาพ:

1. ความไม่สมมาตร

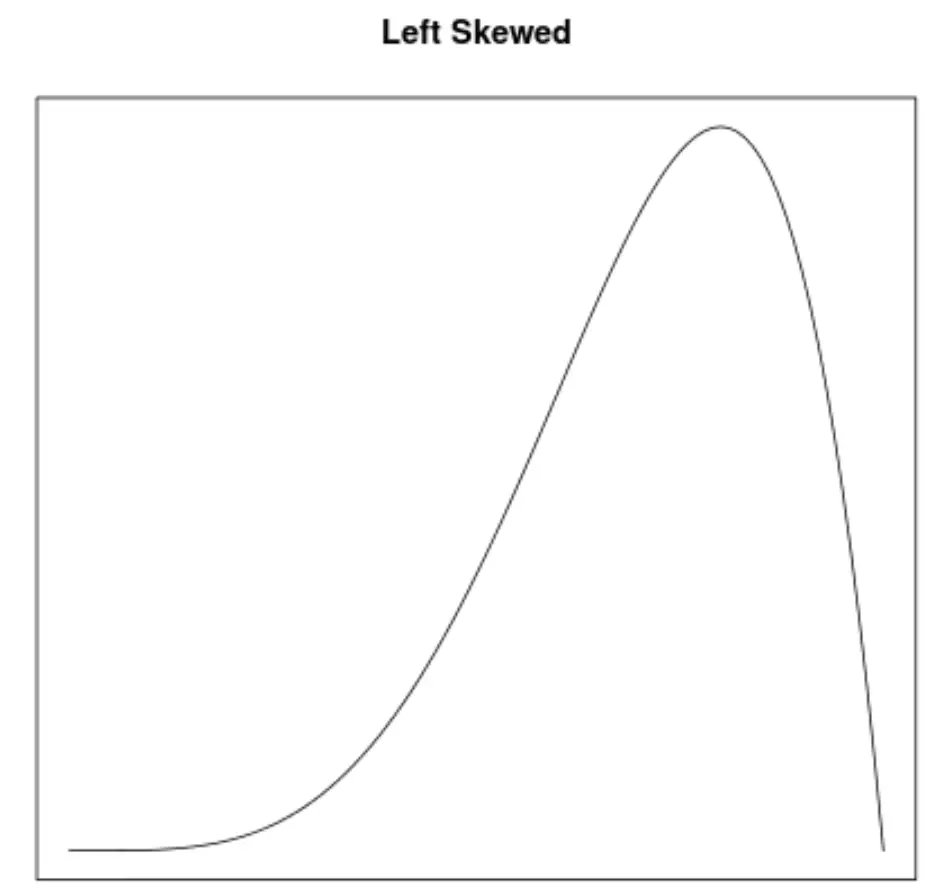
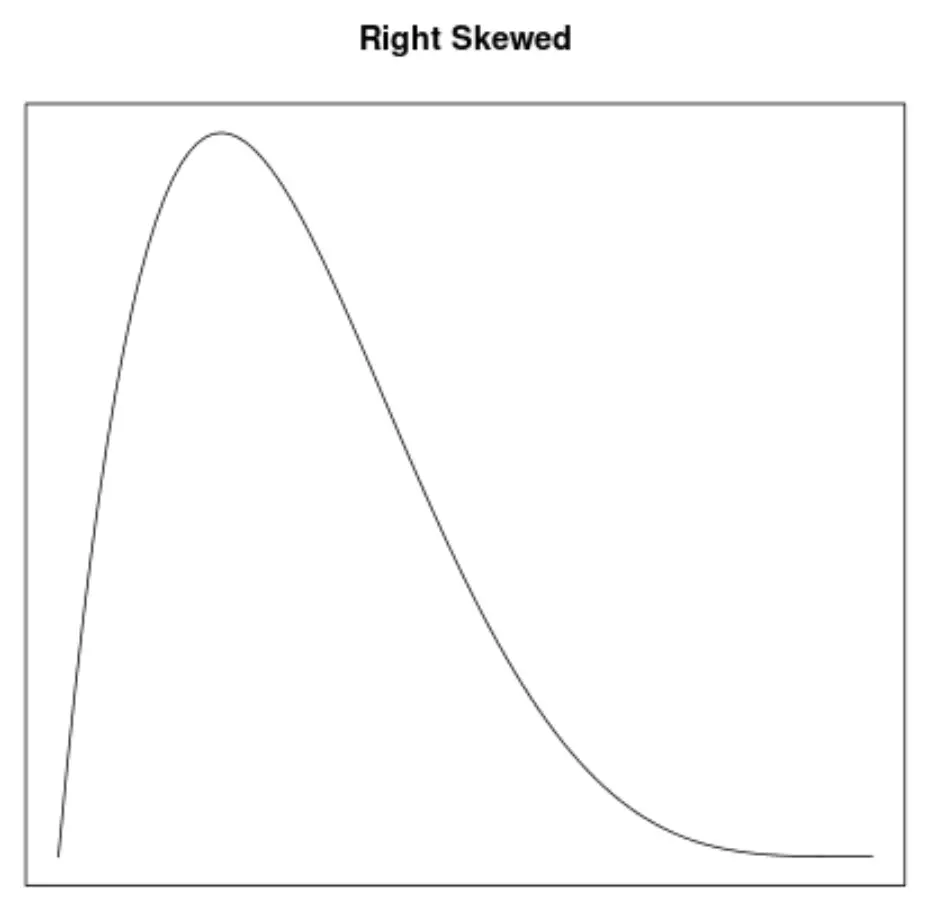
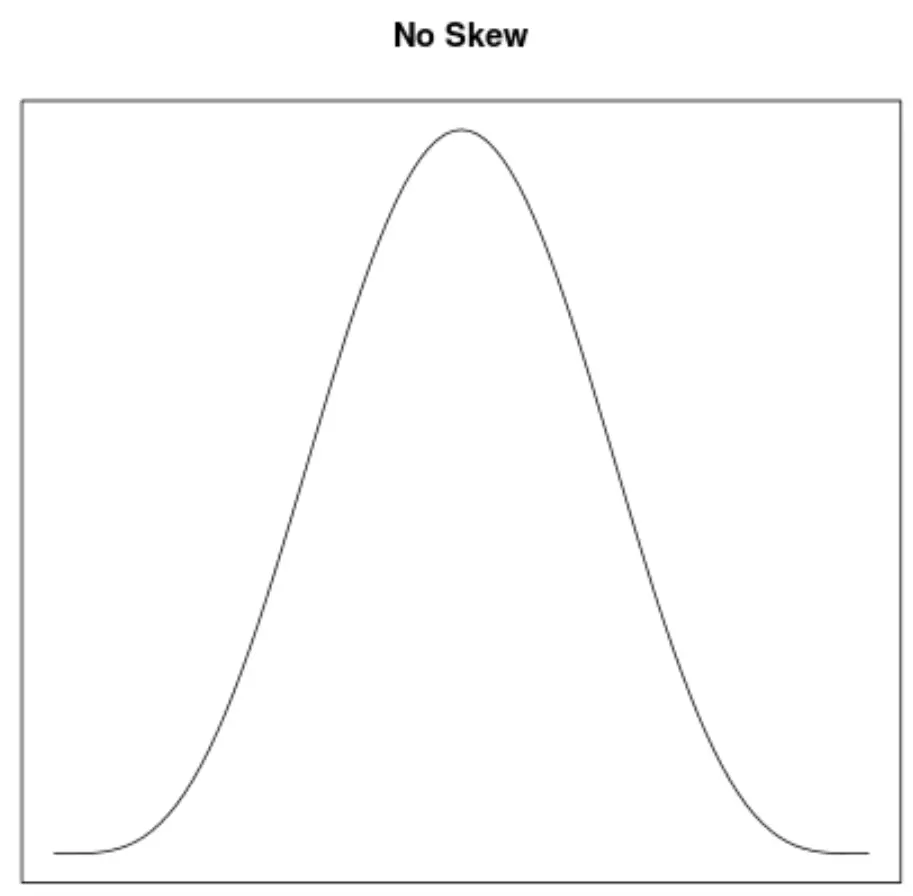
ความเบ้เป็นวิธีหนึ่งในการอธิบายความสมมาตรของการแจกแจง เส้นโค้งความหนาแน่นช่วยให้เราเห็นได้อย่างรวดเร็วว่ากราฟเอียงไปทางซ้าย ขวา หรือไม่มีความเอียง:

2. ตำแหน่งของค่าเฉลี่ยและค่ามัธยฐาน

จากความเบ้ของเส้นโค้งความหนาแน่น เราสามารถบอกได้อย่างรวดเร็วว่าค่าเฉลี่ยหรือค่ามัธยฐานมีค่ามากกว่าในการแจกแจงที่กำหนด โดยเฉพาะ:

• หากเส้นโค้งความหนาแน่น ยังคงไม่สมมาตร แสดงว่าค่าเฉลี่ยจะ ต่ำกว่า ค่ามัธยฐาน
• หากเส้นโค้งความหนาแน่น เอียงไปทางขวา แสดงว่าค่าเฉลี่ยจะ มากกว่า ค่ามัธยฐาน
• หากเส้นโค้งความหนาแน่น ไม่มีความไม่สมมาตร ค่าเฉลี่ยจะ เท่ากับ ค่ามัธยฐาน

3. จำนวนพีค

เส้นโค้งความหนาแน่นยังช่วยให้เราเห็นได้อย่างรวดเร็วว่ามี “ยอด” จำนวนเท่าใดในการแจกแจงที่กำหนด ในแต่ละตัวอย่างข้างต้น การแจกแจงมียอดเพียงจุดเดียว ดังนั้นเราจะอธิบายการแจกแจงเหล่านี้เป็น แบบยูนิโมดัล

อย่างไรก็ตาม การแจกแจงบางแบบอาจมีพีคสองค่าซึ่งเราเรียกว่า การแจกแจงแบบไบโมดัล และในบางกรณีที่เกิดขึ้นไม่บ่อยนัก เราก็สามารถมี การแจกแจง แบบหลายรูป แบบที่มียอดสองค่าขึ้นไปได้

เพียงสร้างกราฟความหนาแน่นสำหรับชุดข้อมูลที่กำหนด เราก็สามารถดูจำนวนพีคในการแจกแจงได้อย่างรวดเร็ว

คุณสมบัติของเส้นโค้งความหนาแน่น

เส้นโค้งความหนาแน่นมีคุณสมบัติดังต่อไปนี้:

• พื้นที่ใต้เส้นโค้งจะรวมกันได้ 100% เสมอ
• เส้นโค้งจะไม่ต่ำกว่าแกน x

โปรดคำนึงถึงข้อเท็จจริงทั้งสองนี้เมื่อสร้างหรือตีความเส้นโค้งความหนาแน่นสำหรับการแจกแจงที่แตกต่างกัน

แหล่งข้อมูลเพิ่มเติม

รู้เบื้องต้นเกี่ยวกับฮิสโตแกรมความถี่สัมพัทธ์
วิธีการสร้างเส้นโค้งระฆังใน Excel
วิธีสร้าง Bell Curve ใน Python