วิธีสร้างและตีความ roc curve ใน spss

การถดถอยแบบลอจิสติก เป็นวิธีการทางสถิติที่เราใช้เพื่อปรับให้เหมาะสมกับแบบจำลองการถดถอยเมื่อตัวแปรตอบสนองเป็นไบนารี เพื่อประเมินว่าแบบจำลองการถดถอยโลจิสติกเหมาะสมกับชุดข้อมูลได้ดีเพียงใด เราสามารถดูตัวชี้วัดสองตัวต่อไปนี้:

• ความไว: ความน่าจะเป็นที่แบบจำลองคาดการณ์ผลลัพธ์ที่เป็นบวกสำหรับการสังเกต เมื่อผลลัพธ์เป็นบวกจริงๆ
• ความจำเพาะ: ความน่าจะเป็นที่แบบจำลองทำนายผลลัพธ์ที่เป็นลบสำหรับการสังเกต เมื่อผลลัพธ์เป็นลบจริงๆ

วิธีง่ายๆ ในการแสดงภาพเมตริกทั้งสองนี้คือการสร้าง เส้นโค้ง ROC ซึ่งเป็นกราฟที่แสดงความไวและความเฉพาะเจาะจงของแบบจำลองการถดถอยลอจิสติก

บทช่วยสอนนี้จะอธิบายวิธีสร้างและตีความเส้นโค้ง ROC ใน SPSS

ตัวอย่าง: เส้นโค้ง ROC ใน SPSS

สมมติว่าเรามีชุดข้อมูลต่อไปนี้ที่แสดงว่าผู้เล่นบาสเก็ตบอลถูกดราฟท์เข้าสู่ NBA หรือไม่ (0 = ไม่, 1 = ใช่) รวมถึงคะแนนต่อเกมโดยเฉลี่ยในวิทยาลัย:

หากต้องการสร้างเส้นโค้ง ROC สำหรับชุดข้อมูลนี้ คลิกแท็บ วิเคราะห์ จากนั้น จัดประเภท จากนั้น ROC Curve :

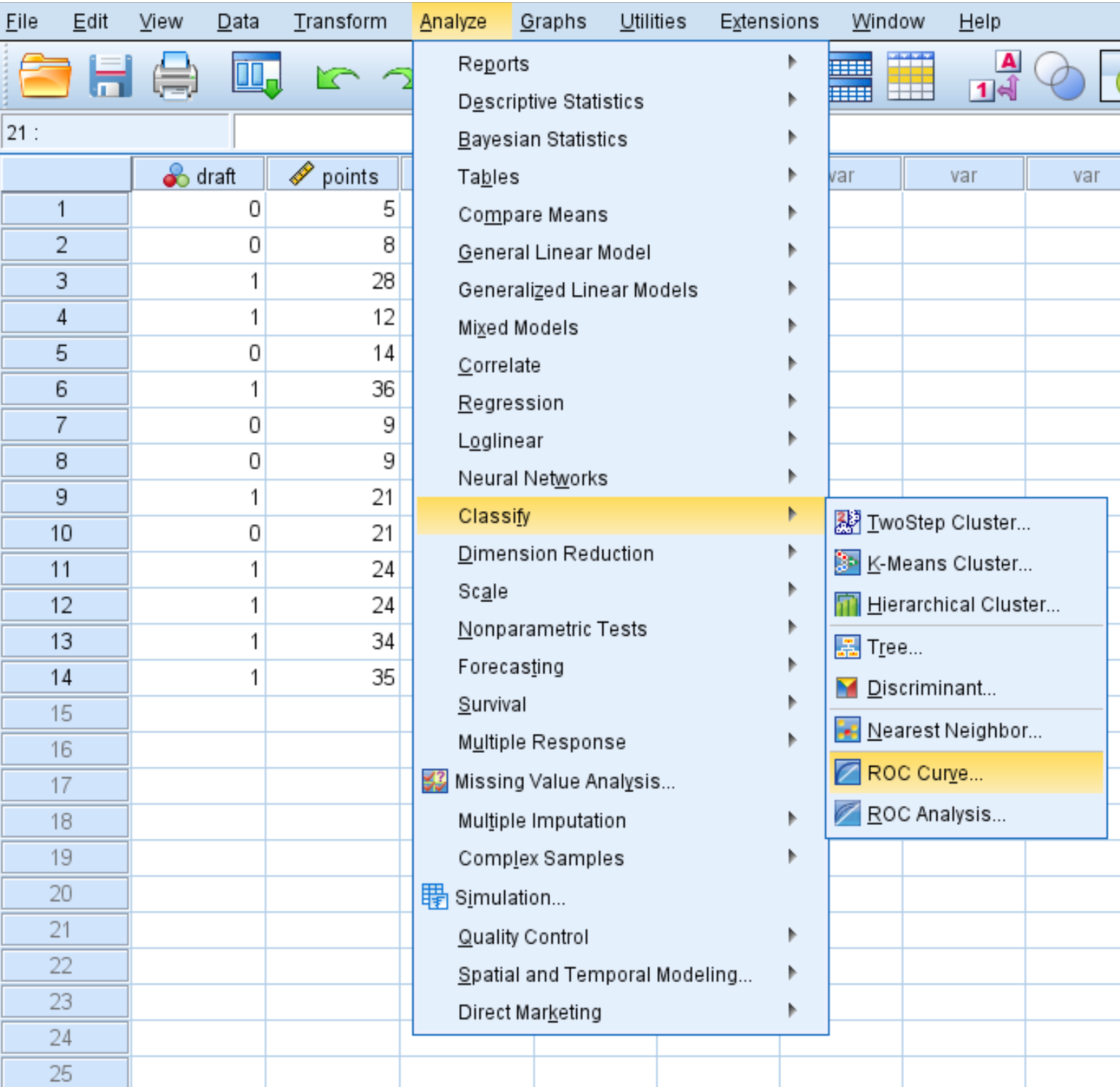
ในหน้าต่างใหม่ที่ปรากฏขึ้น ให้ลากตัวแปร แบบร่าง ลงในพื้นที่ที่ชื่อตัวแปรสถานะ ตั้งค่าของตัวแปรสถานะเป็น 1 (นี่คือค่าที่บ่งบอกว่าผู้เล่นได้รับการดราฟต์แล้ว) ลาก จุด ตัวแปรลงในพื้นที่ที่ชื่อตัวแปรทดสอบ

ทำเครื่องหมายที่ช่องถัดจาก ด้วยเส้นอ้างอิงแนวทแยง และ พิกัดเส้นโค้ง ROC จากนั้นคลิก ตกลง

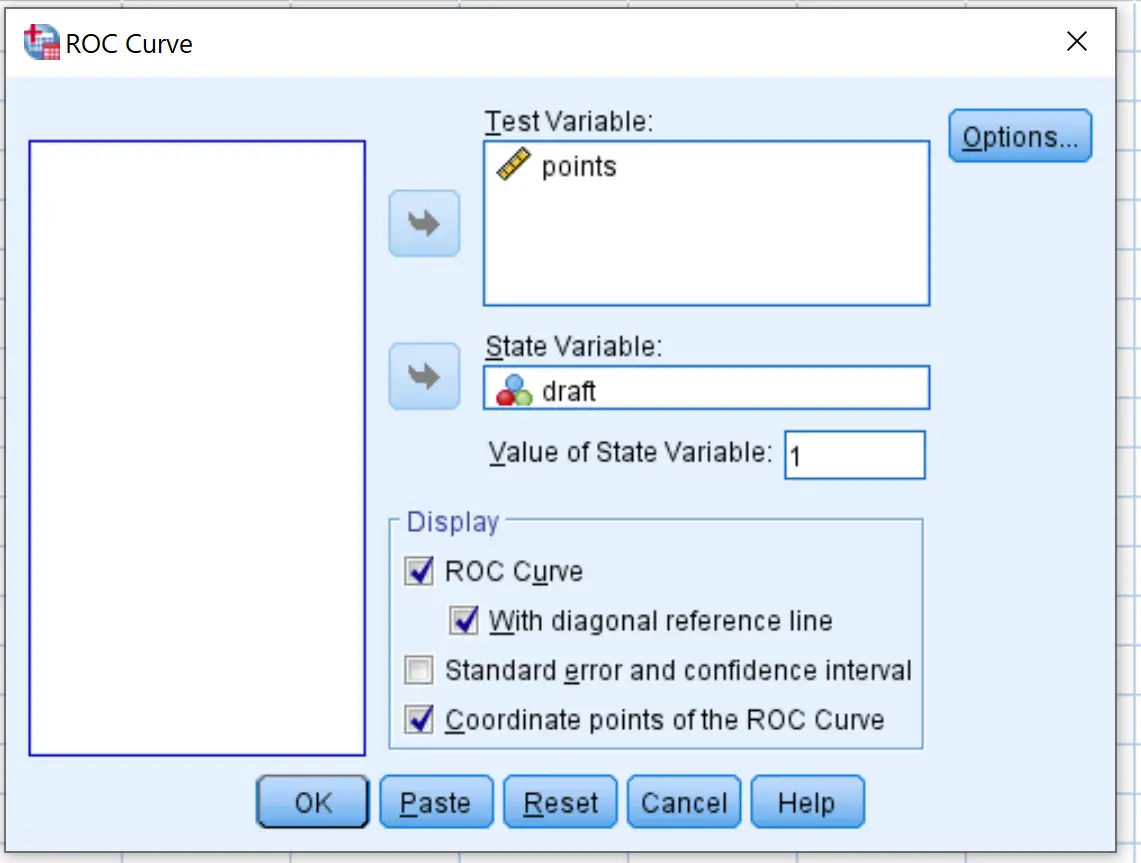
ต่อไปนี้เป็นวิธีการตีความผลลัพธ์:

สรุปการประมวลผลไฟล์:

ตารางนี้แสดงจำนวนกรณีบวกและลบทั้งหมดในชุดข้อมูล ในตัวอย่างนี้ ผู้เล่น 8 คนถูกดราฟท์ (ผลเป็นบวก) และผู้เล่น 6 คนไม่ถูกดราฟท์ (ผลลบ):

เส้นโค้ง ROC:

เส้นโค้งลักษณะการทำงานของตัวรับ (ROC) คือพล็อตของค่าความไวเทียบกับความจำเพาะ 1 เนื่องจากค่าเกณฑ์เปลี่ยนจาก 0 เป็น 1:

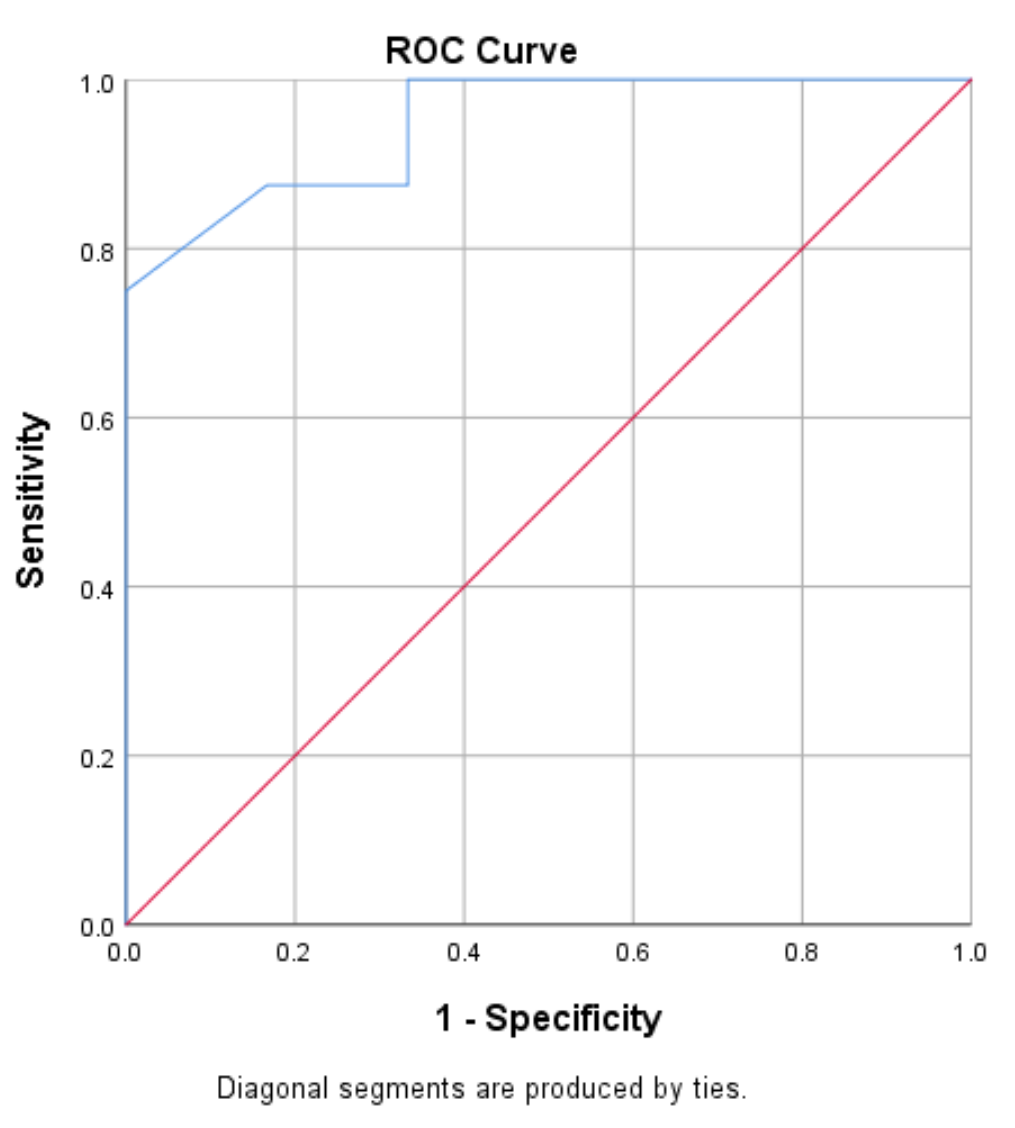
โมเดลที่มีความไวและความจำเพาะสูงจะมีเส้นโค้ง ROC ที่พอดีกับมุมซ้ายบนของโครงเรื่อง แบบจำลองที่มีความไวต่ำและความจำเพาะต่ำจะมีเส้นโค้งใกล้กับเส้นทแยงมุม 45 องศา

เราจะเห็นได้ว่าเส้นโค้ง ROC (เส้นสีน้ำเงิน) ในตัวอย่างนี้โอบมุมซ้ายบนของโครงเรื่อง ซึ่งบ่งชี้ว่าแบบจำลองทำงานได้ดีในการทำนายผู้เล่นว่าจะถูกร่างหรือไม่ โดยพิจารณาจากคะแนนเฉลี่ยต่อเกม . .

พื้นที่ใต้เส้นโค้ง:

พื้นที่ใต้เส้นโค้งทำให้เราเข้าใจถึงความสามารถของแบบจำลองในการแยกแยะระหว่างผลลัพธ์เชิงบวกและเชิงลบ AUC สามารถอยู่ในช่วงตั้งแต่ 0 ถึง 1 ยิ่ง AUC สูงเท่าใด โมเดลก็จะยิ่งจำแนกผลลัพธ์ได้อย่างถูกต้องมากขึ้นเท่านั้น

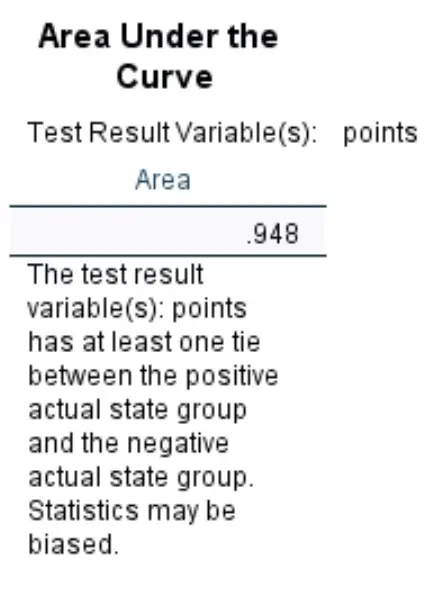
เราจะเห็นว่า AUC สำหรับแบบจำลองการถดถอยโลจิสติกเฉพาะนี้คือ 0.948 ซึ่งสูงมาก สิ่งนี้บ่งชี้ว่าโมเดลนี้คาดการณ์ได้ดีว่าผู้เล่นจะถูกดราฟต์หรือไม่

พิกัดเส้นโค้ง:

ตารางสุดท้ายนี้แสดงความไวและความเฉพาะเจาะจง 1 ของเส้นโค้ง ROC สำหรับเกณฑ์ที่แตกต่างกัน

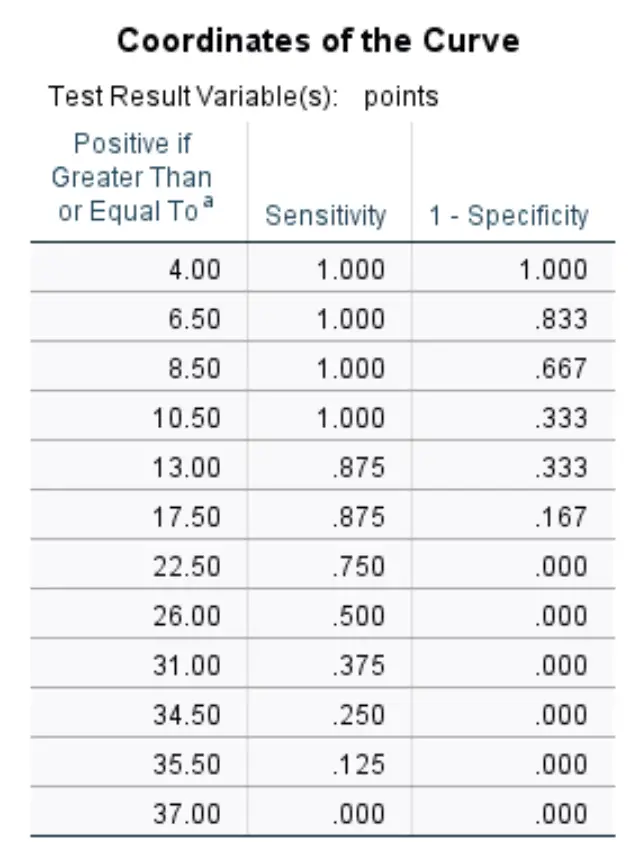
ตัวอย่างเช่น:

หากเราอนุญาตให้เกณฑ์เป็น 8.50 หมายความว่าเราคาดหวังว่าผู้เล่นที่ทำคะแนนน้อยกว่า 8.50 แต้มต่อเกมจะไม่ถูกดราฟท์ และผู้เล่นที่ทำคะแนนมากกว่า 8.50 แต้มต่อเกมจะถูกดราฟต์

การใช้สิ่งนี้เป็นเกณฑ์ ความอ่อนไหว ของเราจะเป็น 100% (เนื่องจากผู้เล่นทุกคนที่ทำคะแนนน้อยกว่า 8.50 คะแนนต่อเกมไม่ได้ถูกเกณฑ์ทหาร) และ ความจำเพาะของเรา 1 จะเป็น 66.7% (เนื่องจากผู้เล่น 8 คนจาก 12 คนที่ทำคะแนนได้มากกว่า 8.50 คะแนน) ต่อเกมถูกร่างไว้)

ตารางด้านบนช่วยให้เราเห็นความไวและความเฉพาะเจาะจง 1 สำหรับแต่ละเกณฑ์ที่เป็นไปได้