วิธีแปลงข้อมูลใน r (log, square root, cube root)

การทดสอบทางสถิติจำนวนมากถือว่าส่วนที่เหลือของ ตัวแปรตอบสนอง มีการกระจายตามปกติ

อย่างไรก็ตาม ส่วนที่เหลือมัก ไม่ กระจายตามปกติ วิธีหนึ่งในการแก้ปัญหานี้คือการแปลงตัวแปรการตอบสนองโดยใช้การแปลงแบบใดแบบหนึ่งจากสามแบบ:

1. การแปลงบันทึก: แปลงตัวแปรการตอบสนองจาก y เป็น log(y)

2. การแปลงรากที่สอง: แปลงตัวแปรตอบสนองจาก y เป็น √y

3. การแปลงรากที่สาม: แปลงตัวแปรการตอบสนองจาก y เป็น y ^1/3

โดยการดำเนินการแปลงเหล่านี้ โดยทั่วไปแล้วตัวแปรการตอบสนองจะประมาณค่าการแจกแจงแบบปกติ ตัวอย่างต่อไปนี้แสดงวิธีการดำเนินการแปลงเหล่านี้ใน R

บันทึกการเปลี่ยนแปลงใน R

รหัสต่อไปนี้แสดงวิธีการดำเนินการบันทึกการเปลี่ยนแปลงในตัวแปรตอบสนอง:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform log transformation
log_y <- log10(df$y)

รหัสต่อไปนี้แสดงวิธีการสร้างฮิสโตแกรมเพื่อแสดงการกระจายของ y ก่อนและหลังการดำเนินการบันทึกการแปลง:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for log-transformed distribution 
hist(log_y, col='coral2', main='Log Transformed')

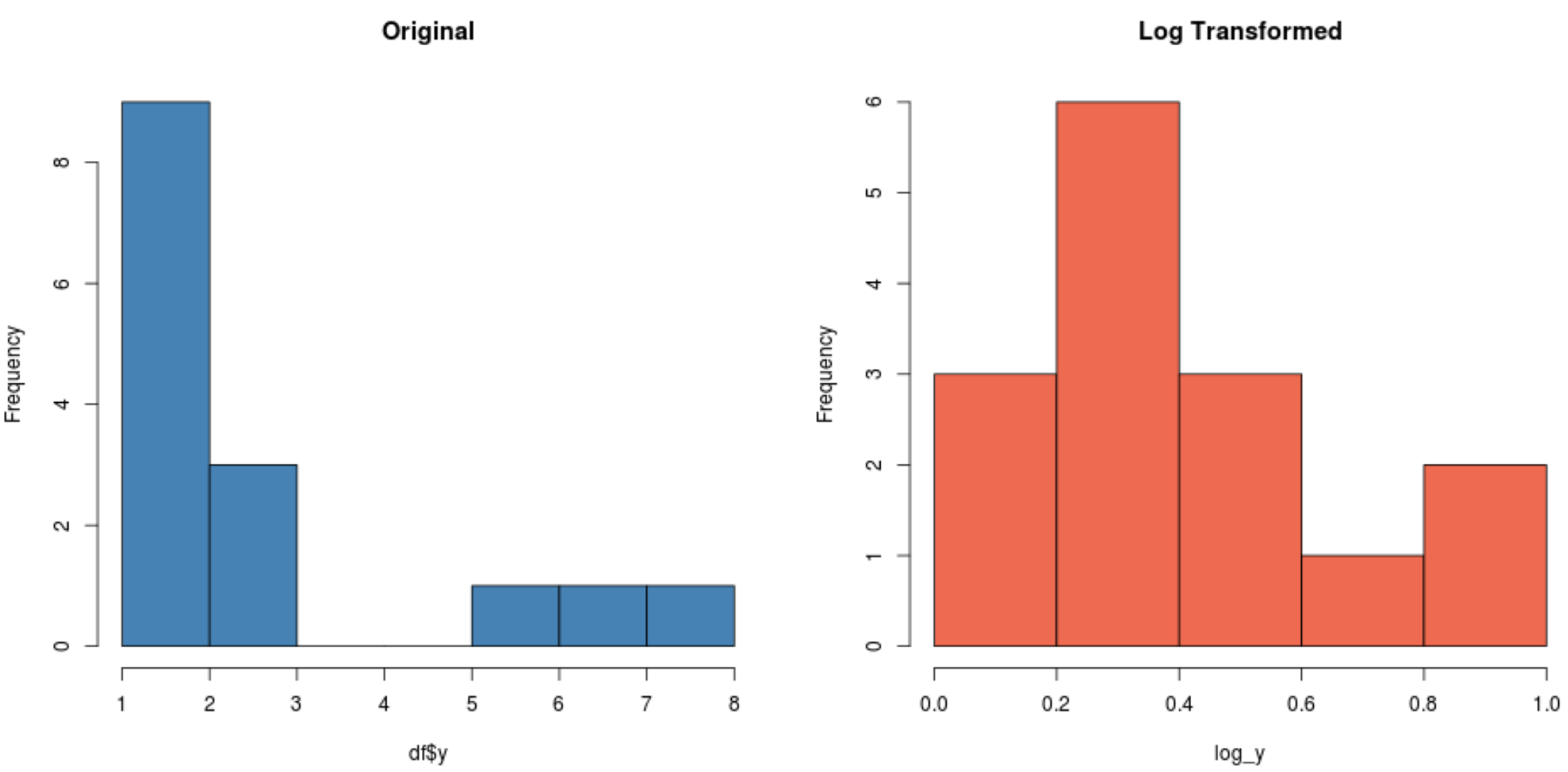
สังเกตว่าการแจกแจงที่แปลงบันทึกนั้นปกติมากกว่าการแจกแจงดั้งเดิมอย่างไร มันยังไม่ใช่ “รูปทรงระฆัง” ที่สมบูรณ์แบบแต่มีความใกล้เคียงกับการกระจายตัวแบบปกติมากกว่าการกระจายตัวแบบเดิม

ในความเป็นจริง หากเราทำการ ทดสอบชาปิโร-วิลค์ ในการแจกแจงแต่ละครั้ง เราจะพบว่าการแจกแจงแบบเดิมไม่เป็นไปตามสมมติฐานปกติ ในขณะที่การแจกแจงแบบแปลงบันทึกไม่ (ที่ α = 0.05):

 #perform Shapiro-Wilk Test on original data
shapiro.test(df$y)

	Shapiro-Wilk normality test

data: df$y
W = 0.77225, p-value = 0.001655

#perform Shapiro-Wilk Test on log-transformed data 
shapiro.test(log_y)

	Shapiro-Wilk normality test

data:log_y
W = 0.89089, p-value = 0.06917

การแปลงรากที่สองใน R

รหัสต่อไปนี้แสดงวิธีการดำเนินการแปลงรากที่สองในตัวแปรตอบสนอง:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
sqrt_y <- sqrt(df$y)

รหัสต่อไปนี้แสดงวิธีการสร้างฮิสโตแกรมเพื่อแสดงการแจกแจงของ y ก่อนและหลังการดำเนินการแปลงรากที่สอง:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(sqrt_y, col='coral2', main='Square Root Transformed') 

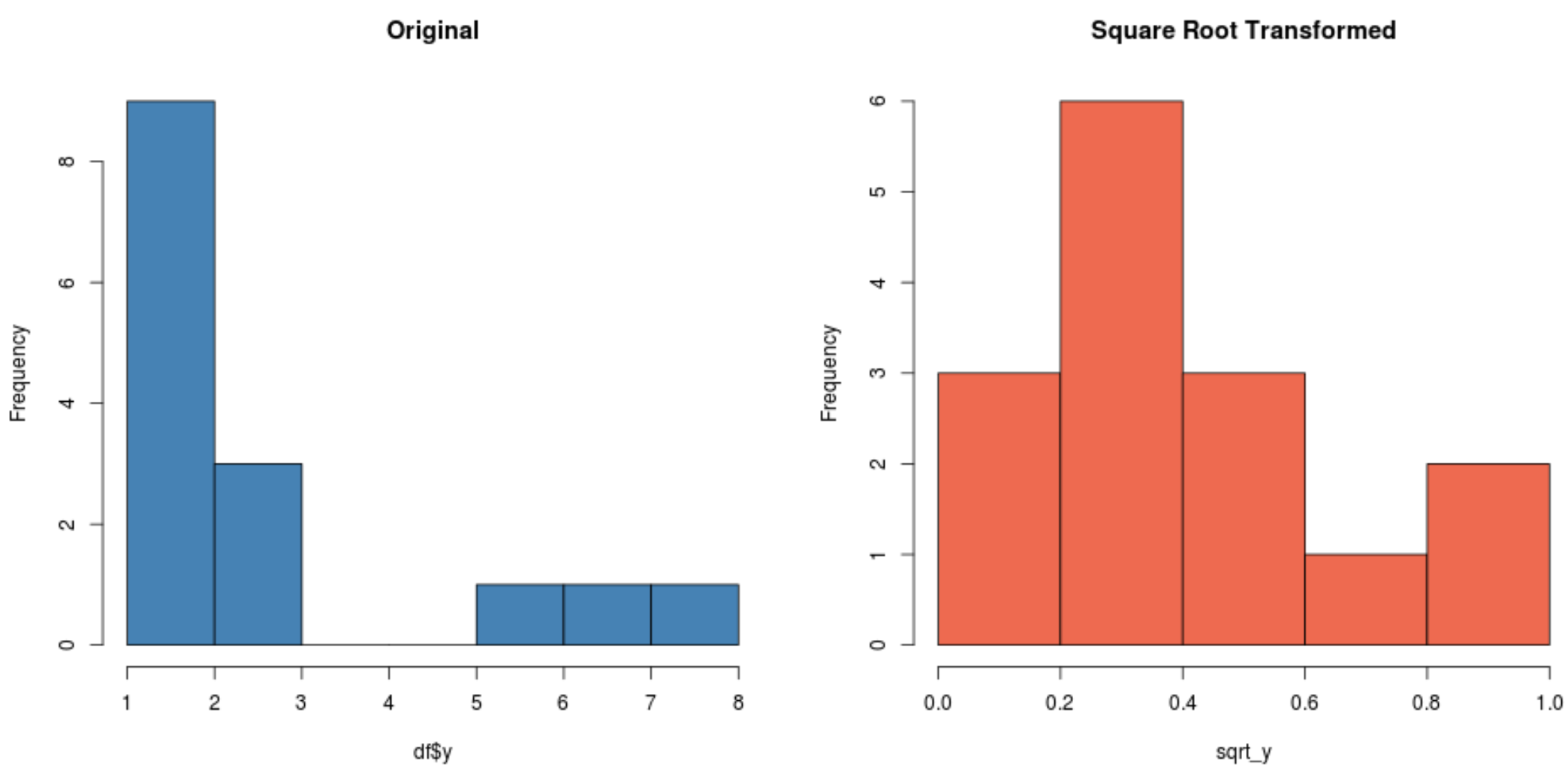
สังเกตว่าการกระจายตัวที่แปลงรูปรากที่สองนั้นมีการกระจายแบบปกติมากกว่าการกระจายตัวแบบเดิมมากอย่างไร

การแปลงรากที่สามใน R

รหัสต่อไปนี้แสดงวิธีการดำเนินการแปลงรากของคิวบ์บนตัวแปรตอบสนอง:

 #create data frame
df <- data.frame(y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8),
                 x1=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8),
                 x2=c(3, 3, 6, 6, 8, 9, 9, 8, 8, 7, 4, 3, 3, 2, 7))

#perform square root transformation
cube_y <- df$y^(1/3)

รหัสต่อไปนี้แสดงวิธีการสร้างฮิสโตแกรมเพื่อแสดงการแจกแจงของ y ก่อนและหลังการดำเนินการแปลงรากที่สอง:

 #create histogram for original distribution
hist(df$y, col='steelblue', main='Original')

#create histogram for square root-transformed distribution 
hist(cube_y, col='coral2', main='Cube Root Transformed') 

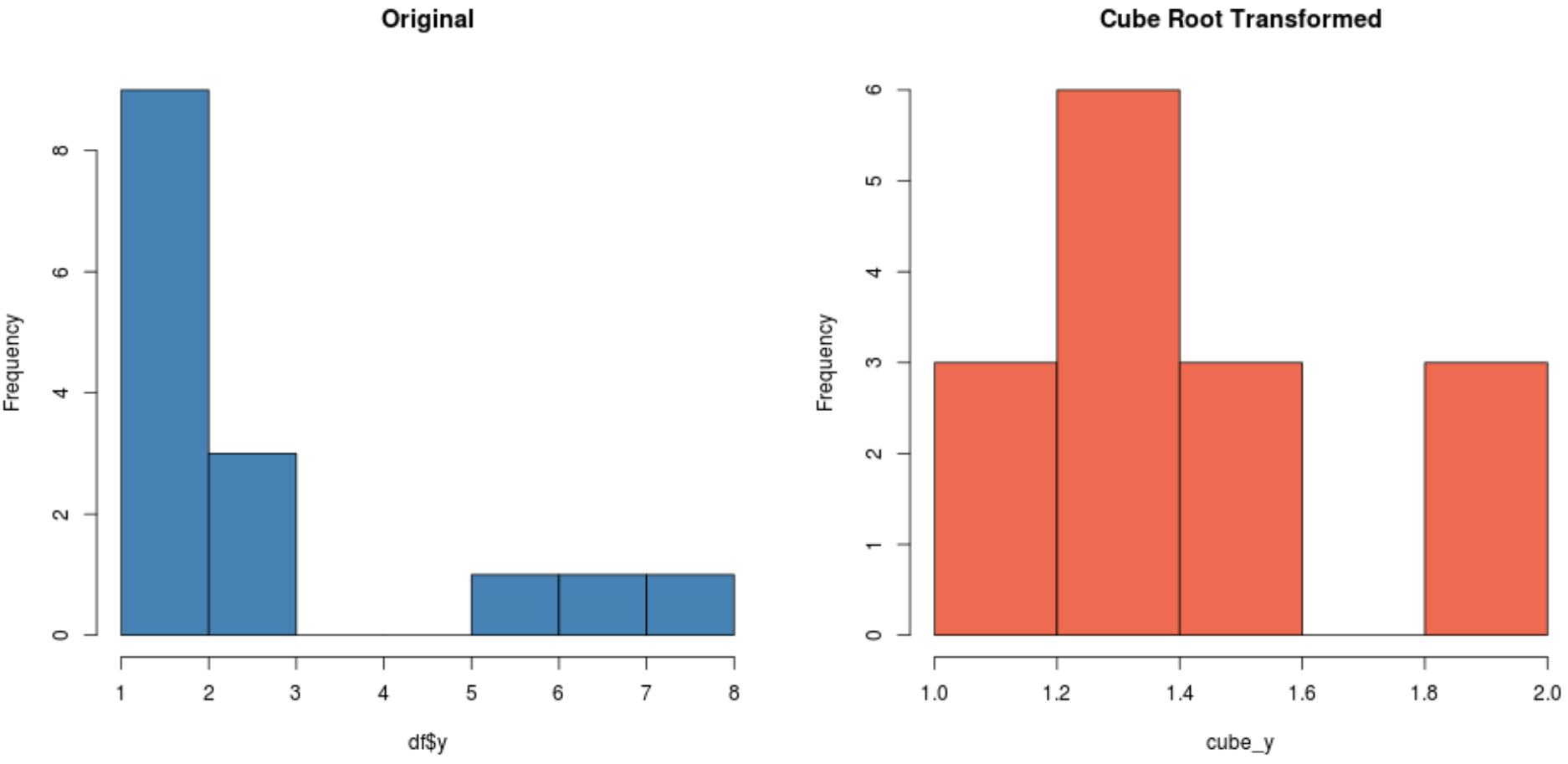
การแปลงอย่างใดอย่างหนึ่งเหล่านี้อาจสร้างชุดข้อมูลใหม่ที่มีการกระจายตามปกติมากกว่าชุดอื่นๆ ทั้งนี้ขึ้นอยู่กับชุดข้อมูลของคุณ