วิธีการตีความแผนการวินิจฉัยใน r

แบบจำลองการถดถอยเชิงเส้นใช้เพื่ออธิบายความสัมพันธ์ระหว่างตัวแปรทำนายหนึ่งตัวขึ้นไปกับตัวแปรตอบสนอง

อย่างไรก็ตาม เมื่อเราติดตั้งแบบจำลองการถดถอยแล้ว เป็นความคิดที่ดีที่จะสร้าง แผนการวินิจฉัย เพื่อวิเคราะห์ส่วนที่เหลือของแบบจำลอง และตรวจสอบให้แน่ใจว่าแบบจำลองเชิงเส้นมีความเหมาะสมที่จะใช้กับข้อมูลเฉพาะที่เรากำลังดำเนินการอยู่

บทช่วยสอนนี้จะอธิบายวิธีสร้างและตีความแผนการวินิจฉัยสำหรับแบบจำลองการถดถอยที่ระบุใน R

ตัวอย่าง: สร้างและตีความแผนการวินิจฉัยใน R

สมมติว่าเราใช้แบบจำลองการถดถอยเชิงเส้นอย่างง่ายโดยใช้ “ชั่วโมงเรียน” เพื่อทำนาย “เกรดสอบ” ของนักเรียนในชั้นเรียนหนึ่งๆ:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

เราสามารถใช้คำสั่ง plot() เพื่อสร้างแผนการวินิจฉัยสี่แผนสำหรับโมเดลการถดถอยนี้:

 #produce diagnostic plots for regression model
plot(model)

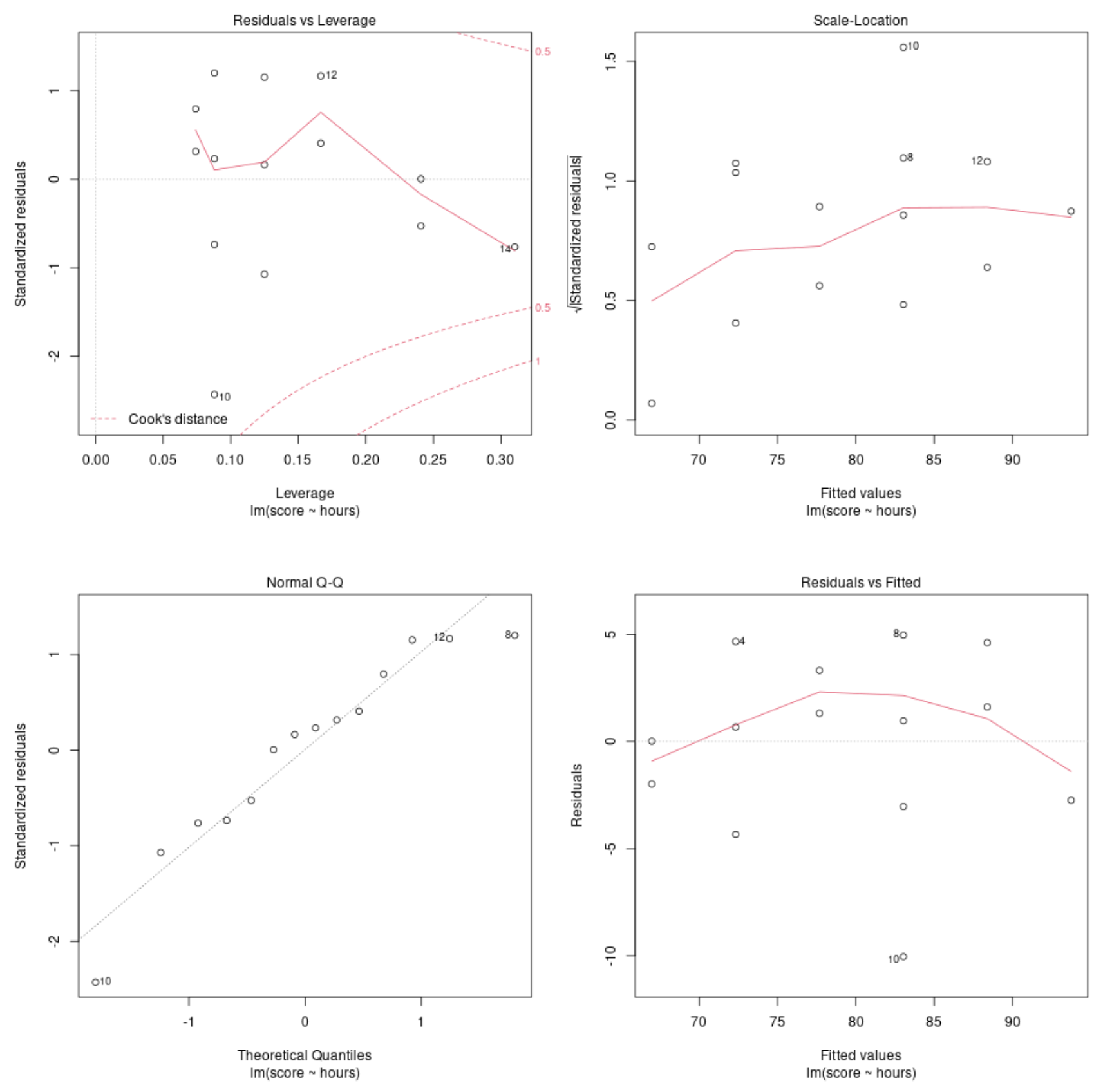
แผนภูมิการวินิจฉัย #1: สิ่งตกค้างเทียบกับ แผนภูมิเลเวอเรจ

กราฟนี้ใช้เพื่อระบุการสังเกตที่มีอิทธิพล หากจุดใดๆ บนกราฟนี้อยู่นอกระยะห่างของคุก (เส้นประ) แสดงว่านี่เป็นข้อสังเกตที่มีอิทธิพล

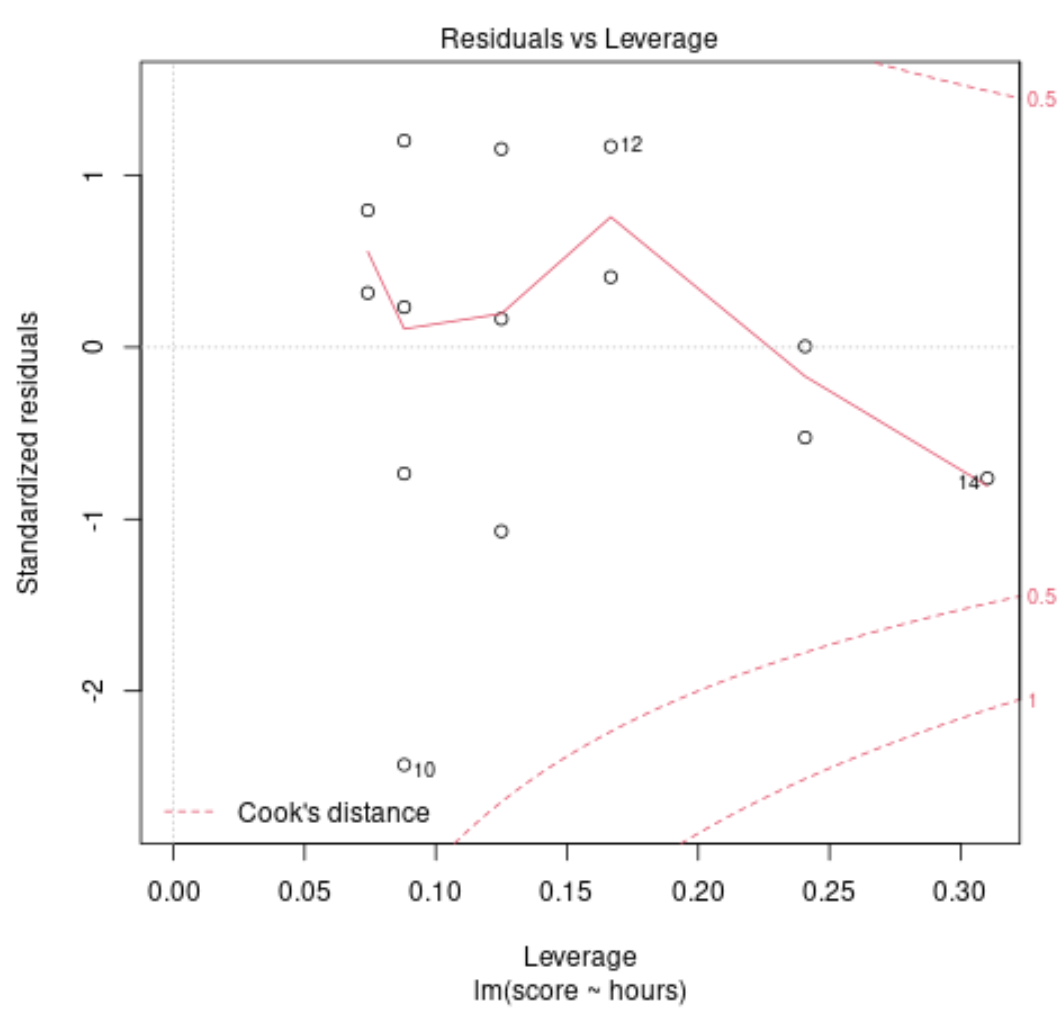
ในตัวอย่างของเรา เราจะเห็นว่าการสังเกต #10 นั้นใกล้กับขีดจำกัดระยะทางของ Cook มากที่สุด แต่ไม่ได้อยู่นอกเส้นประ ซึ่งหมายความว่าไม่มีจุดที่มีอิทธิพลมากเกินไปในชุดข้อมูลของเรา

แผนการวินิจฉัย #2: แผนมาตราส่วนและตำแหน่ง

กราฟนี้ใช้เพื่อตรวจสอบสมมติฐานของความเท่าเทียมกันของความแปรปรวน (หรือที่เรียกว่า “โฮโมสเคดาสติกซิตี้”) ในบรรดาค่าคงเหลือของแบบจำลองการถดถอยของเรา หากเส้นสีแดงอยู่ในแนวนอนโดยประมาณบนโครงเรื่อง ก็อาจเป็นไปตามสมมติฐานของความแปรปรวนที่เท่ากัน

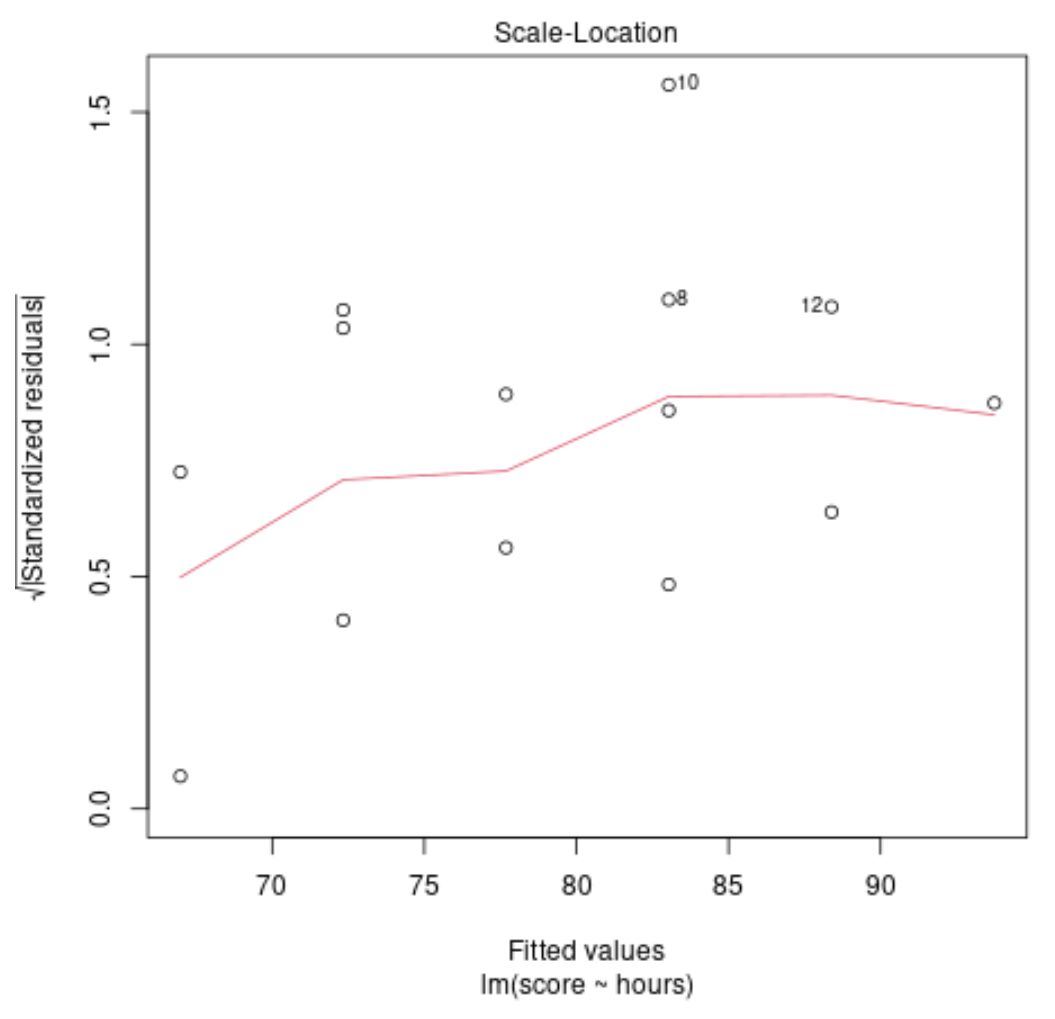
ในตัวอย่างของเรา เราจะเห็นว่าเส้นสีแดงไม่ได้เป็นแนวนอนบนโครงเรื่องทุกประการ แต่ก็ไม่ได้เบี่ยงเบนไปมากจนเกินไปไม่ว่าจุดใดก็ตาม เราอาจระบุว่าในกรณีนี้ข้อสันนิษฐานของความแปรปรวนเท่ากันจะไม่ถูกละเมิด

ที่เกี่ยวข้อง: การทำความเข้าใจ Heteroskedasticity ในการวิเคราะห์การถดถอย

การติดตามการวินิจฉัย #3: การติดตาม QQ ปกติ

พล็อตนี้ใช้เพื่อพิจารณาว่าส่วนที่เหลือจากแบบจำลองการถดถอยมีการกระจายตามปกติหรือไม่ หากจุดบนกราฟนี้อยู่ประมาณตามแนวเส้นทแยงมุมตรง เราก็สามารถสรุปได้ว่าส่วนที่เหลือมีการกระจายตามปกติ

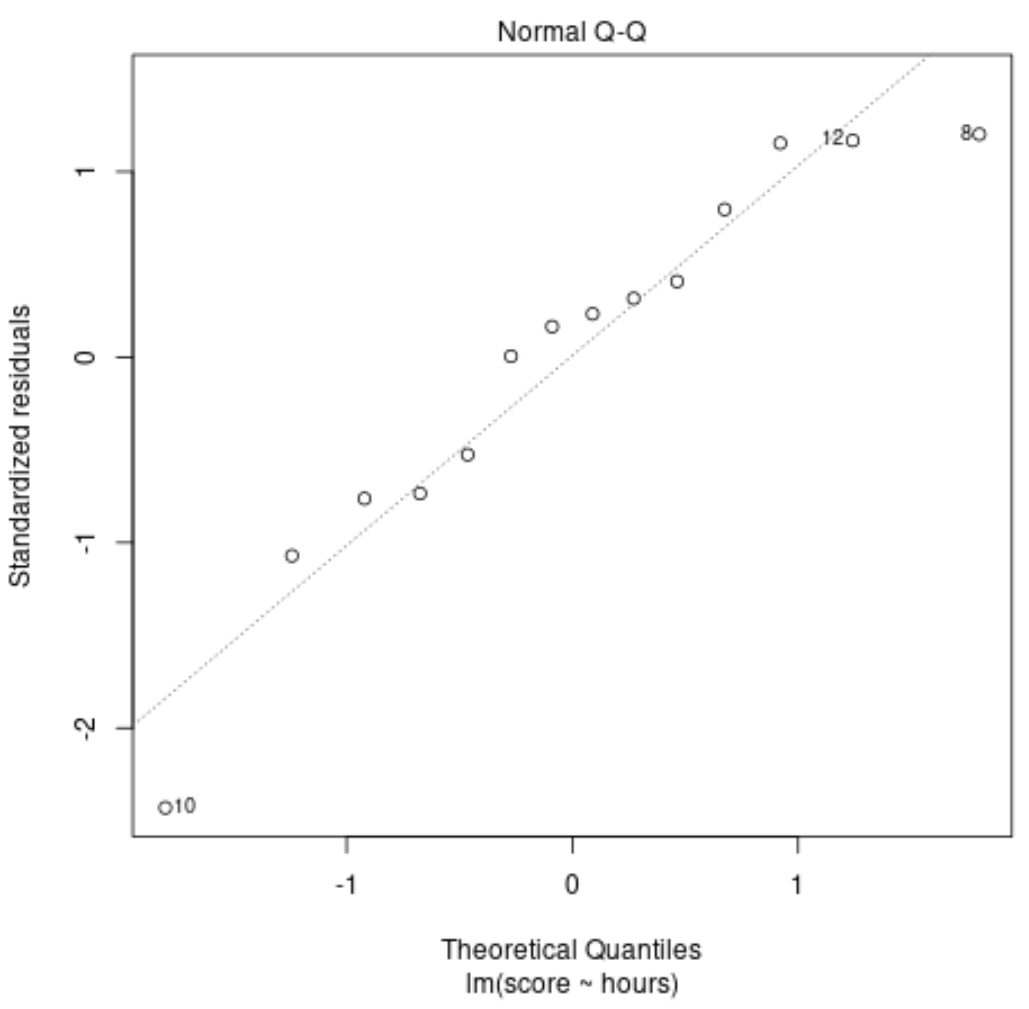
ในตัวอย่างของเรา เราจะเห็นว่าจุดต่างๆ อยู่ประมาณเส้นตรงแนวทแยง ข้อสังเกต #10 และ #8 เบี่ยงเบนเล็กน้อยจากเส้นตรงปลาย แต่ไม่มากพอที่จะประกาศว่าส่วนที่เหลือไม่ได้กระจายตามปกติ

แผนการวินิจฉัย #4: สิ่งตกค้างเทียบกับ ปรับโครงเรื่องแล้ว

แผนภาพนี้ใช้เพื่อพิจารณาว่าสิ่งตกค้างแสดงรูปแบบที่ไม่เป็นเชิงเส้นหรือไม่ ถ้าเส้นสีแดงตรงกลางโครงเรื่องเป็นแนวนอนโดยประมาณ เราสามารถสรุปได้ว่าส่วนที่เหลือเป็นไปตามรูปแบบเส้นตรง

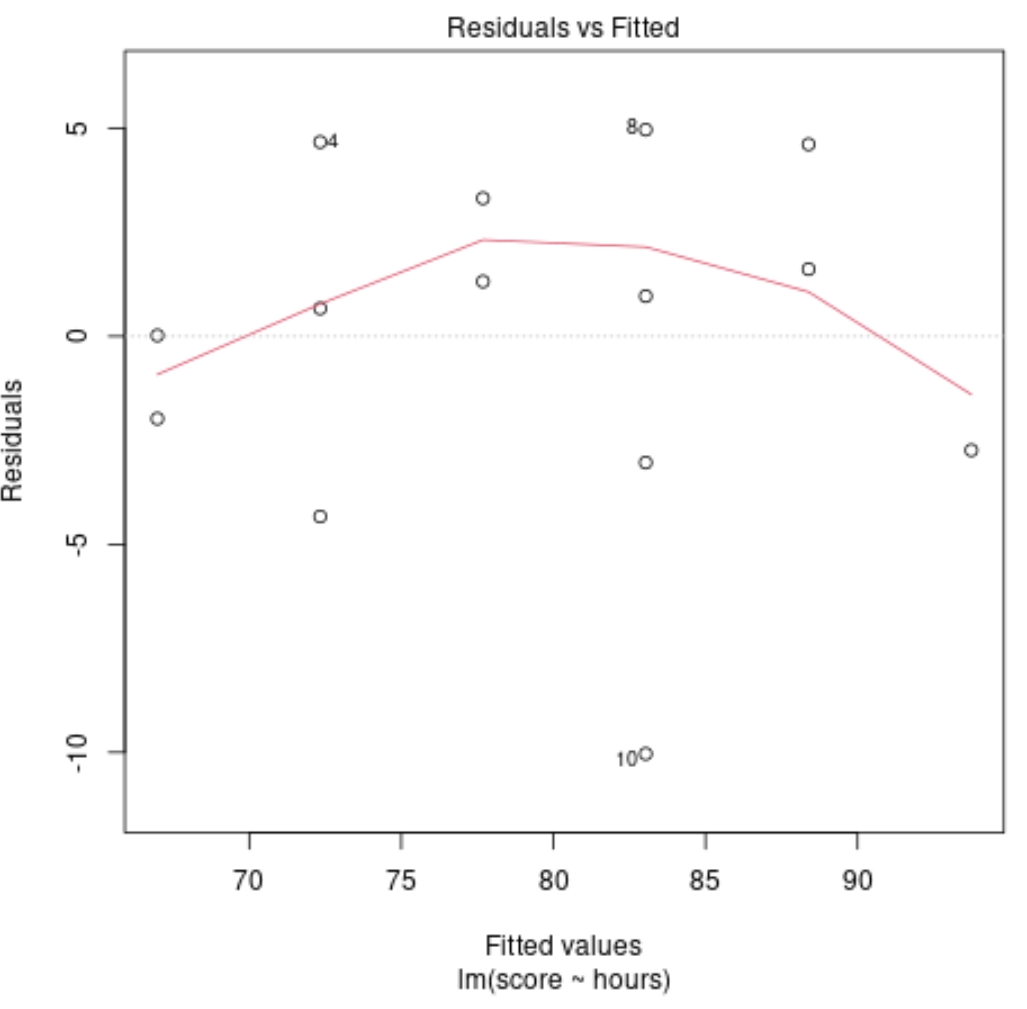
ในตัวอย่างของเรา เราจะเห็นว่าเส้นสีแดงเบี่ยงเบนไปจากเส้นแนวนอนที่สมบูรณ์แต่ไม่มีนัยสำคัญ เรามีแนวโน้มที่จะระบุว่าส่วนที่เหลือเป็นไปตามรูปแบบเชิงเส้นอย่างคร่าว ๆ และแบบจำลองการถดถอยเชิงเส้นมีความเหมาะสมสำหรับชุดข้อมูลนี้

แหล่งข้อมูลเพิ่มเติม

สมมติฐานสี่ประการของการถดถอยเชิงเส้น
สารตกค้างในสถิติคืออะไร?
วิธีสร้างพล็อตที่เหลือใน R
วิธีการตีความมาตราส่วนและแผนผังตำแหน่ง