แผนภาพต้นไม้

บทความนี้จะอธิบายว่าแผนผังต้นไม้คืออะไรและเกิดขึ้นได้อย่างไร ดังนั้นคุณจะพบตัวอย่างโครงสร้างต้นไม้ข้อดีของแผนภาพประเภทนี้และนอกจากนี้แบบฝึกหัดยังแก้ไขได้ทีละขั้นตอน

ต้นไม้คืออะไร?

แผนภาพต้นไม้ หรือที่เรียกว่า แผนผังความน่าจะ เป็น เป็นการแสดงผลลัพธ์ที่เป็นไปได้ทั้งหมดของการทดสอบพร้อมกับความน่าจะเป็นในรูปแบบกราฟิก

ดังนั้น แผนภาพต้นไม้จึงใช้เพื่อสร้างกราฟผลลัพธ์ที่เป็นไปได้ทั้งหมดในพื้นที่ตัวอย่างและคำนวณความน่าจะเป็น

แผนผังต้นไม้ถูกสร้างขึ้นในลักษณะที่แต่ละผลลัพธ์ ( โหนด ) แยกออกเป็นผลลัพธ์ใหม่ที่เป็นไปได้ ( สาขา ) จนกระทั่งถึงผลลัพธ์สุดท้าย

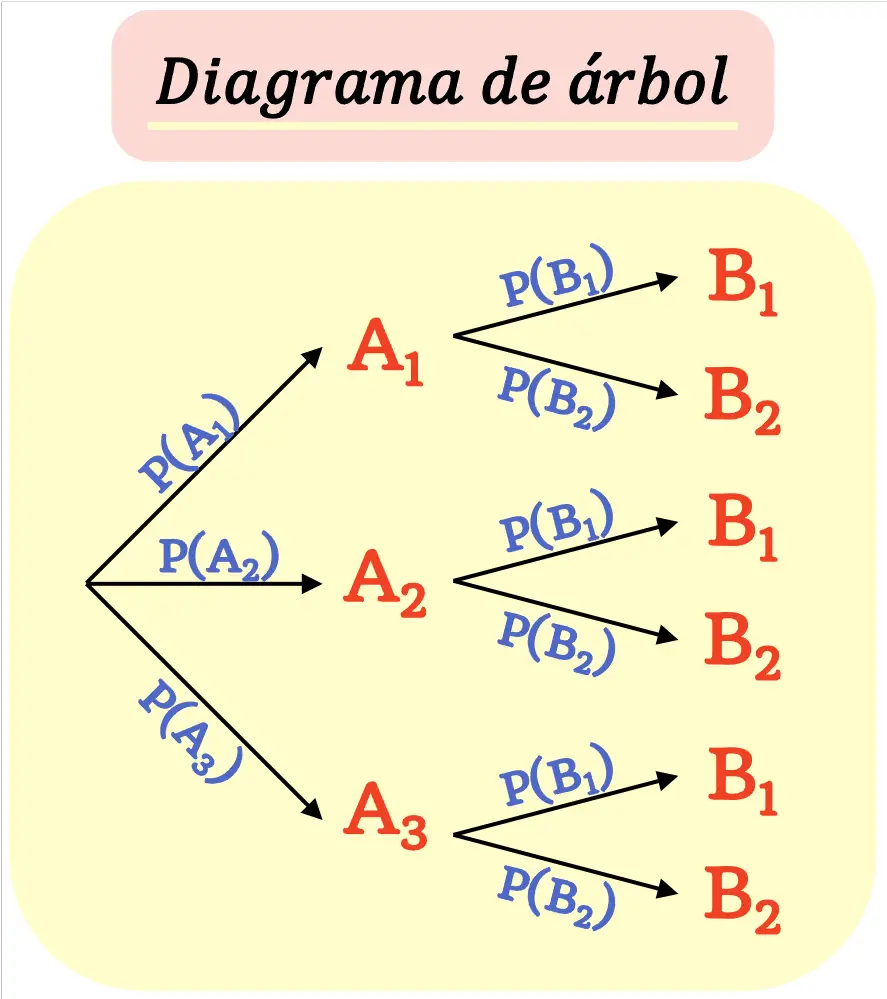
ควรจำไว้ว่าผลรวมของความน่าจะเป็นของสาขาทั้งหมดที่ออกมาจากโหนดจะต้องเท่ากับ 1

วิธีทำไดอะแกรมต้นไม้

หากต้องการ สร้างต้นไม้ คุณต้องทำตามขั้นตอนต่อไปนี้:

1. ขั้นตอนแรกในการสร้างแผนภาพต้นไม้คือการวาดกิ่งก้านสำหรับผลลัพธ์ที่เป็นไปได้แต่ละรายการ ซึ่งจะเป็นสาขารุ่นแรก
2. จากนั้น ความน่าจะเป็นที่เกี่ยวข้องกับแต่ละเหตุการณ์จะถูกเพิ่มเข้าไปในสาขาที่เกี่ยวข้อง
3. จุดสิ้นสุดของแต่ละสาขารุ่นแรกคือโหนดซึ่งจะต้องแสดงสาขาของเหตุการณ์ที่เป็นไปได้ในภายหลัง
4. เช่นเดียวกับสาขาแรก เราต้องเพิ่มความน่าจะเป็นของเหตุการณ์ที่นำเสนอ
5. ทำซ้ำขั้นตอนที่ 3 และ 4 จนกระทั่งถึงโหนดสุดท้าย เช่น จุดสิ้นสุดของการทดสอบที่เป็นไปได้

โปรดทราบว่าจำนวนสาขาในระดับหนึ่งไม่จำเป็นต้องเท่ากับจำนวนสาขาในระดับอื่น ในทำนองเดียวกัน จำนวนสาขาที่เป็นผลจากผลลัพธ์ที่เป็นไปได้อาจแตกต่างกันแม้จะอยู่ในระดับเดียวกันก็ตาม

ตัวอย่างต้นไม้

ตอนนี้เรารู้คำจำกัดความและทฤษฎีของการสร้างแผนภาพต้นไม้แล้ว เรามาดูตัวอย่างจากโลกแห่งความเป็นจริงทีละขั้นตอนเพื่อทำความเข้าใจแนวคิดนี้กันดีกว่า

• สร้างแผนผังความน่าจะเป็นของการโยนเหรียญจากเหรียญอิสระ 3 เหรียญ จากนั้นหาความน่าจะเป็นที่จะได้หัวจากการเสี่ยงทั้งสามครั้ง

การออกสลากมีเพียงสองผลลัพธ์เท่านั้นที่เราจะออกหัวหรือก้อยได้ ดังนั้น ความน่าจะเป็นที่จะได้หัวหรือก้อยเมื่อโยนเหรียญคือ:

เมื่อเราทราบความน่าจะเป็นของผลลัพธ์ที่เป็นไปได้แล้ว เราจะแสดงแผนภาพต้นไม้ต่อไป

เนื่องจากการทอยเหรียญมีความเป็นอิสระ ความน่าจะเป็นที่จะได้หัวหรือก้อยจะเท่ากันเสมอในการทอยแต่ละครั้ง ดังนั้น ในการสร้างต้นไม้ จะต้องแสดงกิ่งก้านสองกิ่ง (หัวและก้อย) ด้วยความน่าจะเป็นเท่ากันในการโยนแต่ละครั้ง

และเมื่อเราสร้างต้นไม้ได้แล้ว สิ่งที่เราต้องทำคือกำหนดความน่าจะเป็นที่จะได้เหรียญ 3 เหรียญ

ดังนั้น ในกรณีนี้ เราต้องคูณความน่าจะเป็นที่จะได้หัวทั้งหมด เพราะนี่คือความน่าจะเป็นของเส้นทางที่นำเราไปสู่ผลลัพธ์ที่ต้องการ

ดังนั้น ความน่าจะเป็นที่จะได้หัวในการโยนเหรียญทั้ง 3 ครั้ง จึงมีการคำนวณดังนี้

กล่าวโดยสรุป ความน่าจะเป็นที่จะได้หัวสามครั้งติดต่อกันคือ 12.5%

แก้การออกกำลังกายต้นไม้

ในหมู่บ้านมีสถานรับเลี้ยงเด็กเพียง 3 แห่ง โดยเด็ก 60% ไปที่สถานรับเลี้ยงเด็ก A, 30% ไปที่สถานรับเลี้ยงเด็ก B และ 10% ไปที่สถานรับเลี้ยงเด็ก C นอกจากนี้ ในสถานรับเลี้ยงเด็กทั้งสามแห่งนั้น 55% เป็นเด็กผู้หญิง สร้างแผนภูมิต้นไม้และคำนวณความน่าจะเป็นต่อไปนี้:

• ความน่าจะเป็นที่เมื่อสุ่มเลือกเด็กจะเป็นเด็กหญิงจากสถานรับเลี้ยงเด็กบี
• ความน่าจะเป็นที่เมื่อสุ่มเลือกเด็กจากศูนย์รับเลี้ยงเด็กแห่งใดแห่งหนึ่ง จะเป็นเด็กผู้ชาย

โปรดทราบว่าหากสัดส่วนของเด็กผู้หญิงในศูนย์รับเลี้ยงเด็กทั้งหมดคือ 55% เปอร์เซ็นต์ของเด็กผู้ชายจะคำนวณโดยการลบ 1 ลบ 0.55:

ตอนนี้เรารู้ความน่าจะเป็นทั้งหมดแล้ว เราสามารถสร้างแผนผังความน่าจะเป็นที่มีความเป็นไปได้ทั้งหมดได้:

ดังนั้นความน่าจะเป็นที่จะสุ่มเลือกเด็กผู้หญิงจากสถานรับเลี้ยงเด็ก B จึงมีการคำนวณดังนี้:

ในทางกลับกัน เพื่อพิจารณาความน่าจะเป็นของการเลือกเด็กชายในสถานรับเลี้ยงเด็กแห่งใดแห่งหนึ่ง เราต้องค้นหาความน่าจะเป็นในการเลือกเด็กผู้ชายสำหรับสถานรับเลี้ยงเด็กแต่ละแห่งก่อน แล้วจึงบวกเข้าด้วยกัน:

ข้อดีของโครงสร้างต้นไม้

เนื่องจากลักษณะของโครงสร้างต้นไม้ ข้อดีของกราฟสถิติประเภทนี้จึงเป็นดังนี้

• แผนภาพต้นไม้มีประโยชน์มากในการตัดสินใจ
• ความสัมพันธ์ระหว่างผลลัพธ์ที่เป็นไปได้ทั้งหมดสามารถแสดงเป็นภาพกราฟิกได้
• สะดวกมากในการค้นหาสาเหตุของปัญหา
• ทำให้ง่ายต่อการแก้ปัญหาความน่าจะเป็นและสถิติ
• แผนภาพต้นไม้ช่วยจัดระเบียบแนวคิดและวิเคราะห์สถานการณ์