แผนภูมิวงกลม

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าแผนภูมิวงกลมคืออะไร วิธีสร้างแผนภูมิวงกลม นอกจากนี้ คุณจะสามารถดูกราฟสถิติประเภทนี้ทีละขั้นตอนได้

แผนภูมิวงกลมคืออะไร?

แผนภูมิวงกลม หรือ แผนภูมิวงกลม เป็นแผนภาพทางสถิติประเภทหนึ่งที่แสดงข้อมูลด้วยวงกลมที่แบ่งออกเป็นส่วนต่างๆ เพื่อให้มุมของแต่ละส่วนเป็นสัดส่วนกับความถี่ที่สอดคล้องกัน

กล่าวอีกนัยหนึ่ง ยิ่งความถี่ของค่าสูงเท่าใด เซกเตอร์ที่สอดคล้องกันในแผนภาพก็จะยิ่งมากขึ้นเท่านั้น

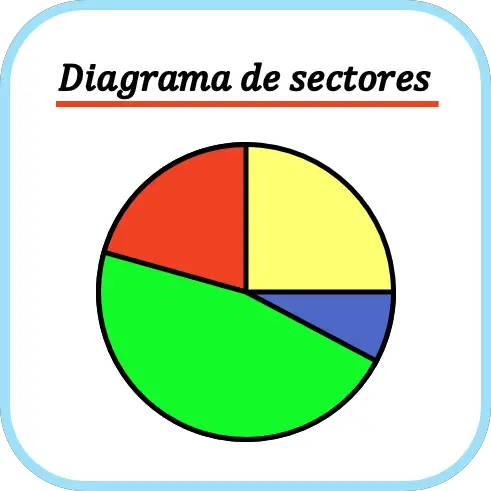
ดังนั้น แผนภูมิวงกลมจึงถูกนำมาใช้เพื่อวิเคราะห์ความถี่ของแต่ละค่าด้วยสายตา ในทางสถิติ กราฟประเภทนี้ส่วนใหญ่จะใช้เพื่อแสดงตัวแปรเชิงคุณภาพ

วิธีทำแผนภูมิวงกลม

ขั้นตอนในการ สร้างแผนภูมิวงกลม มีดังนี้:

รวบรวมข้อมูลทางสถิติจากตัวอย่างที่คุณต้องการวิเคราะห์และสร้างตารางความถี่
คำนวณ มุมของแต่ละส่วนของแผนภาพ เมื่อต้องการทำเช่นนี้ คุณต้องใช้สูตรต่อไปนี้:

$\alpha_i= f_i \cdot \cfrac{360^o}{N}$

ทอง

$\alpha_i$

คือมุมของเซกเตอร์ i

$f_i$

ความถี่สัมบูรณ์และ

$N$

จำนวนข้อมูลทั้งหมด

จากมุมที่คำนวณได้ แสดงภาคต่างๆ ในกราฟวงกลมโดยใช้ไม้โปรแทรกเตอร์มุม
คำนวณ เปอร์เซ็นต์ของแต่ละเซกเตอร์ในแผนภูมิ โดยใช้สูตรต่อไปนี้:

$\%_i= f_i \cdot \cfrac{100}{N}$

ทอง

$\%_i$

คือเปอร์เซ็นต์ของเซกเตอร์ i

$f_i$

ความถี่สัมบูรณ์และ

$N$

จำนวนข้อมูลทั้งหมด

ระบุเปอร์เซ็นต์ของแต่ละเซกเตอร์ในแผนภาพ

ตัวอย่างแผนภูมิวงกลม

เพื่อให้คุณสามารถดูวิธีการสร้างแผนภูมิวงกลมได้อย่างชัดเจน ด้านล่างนี้คือตัวอย่างทีละขั้นตอน:

มีผู้ถูกถาม 50 คนเกี่ยวกับเมืองโปรดของตน และข้อมูลได้รวบรวมไว้ในตารางต่อไปนี้ นำเสนอข้อมูลทางสถิตินี้ในแผนภูมิวงกลม

ก่อนอื่น เราต้องคำนวณมุมที่สอดคล้องกับแต่ละเซกเตอร์ ดังนั้นเราจึงใช้สูตรต่อไปนี้สำหรับแต่ละค่า:

$\alpha_i = f_i \cdot \cfrac{360^o}{N}$

ทอง

$\alpha_i$

คือมุมของแต่ละเซกเตอร์

$f_i$

ความถี่และ

$N$

จำนวนการสังเกตทั้งหมด

ตัวอย่างเช่น การคำนวณมุมของเซกเตอร์ซึ่งสอดคล้องกับค่าแรกคือ:

$\alpha_{Londres}=16 \cdot \cfrac{360^o}{50} = 115,2^o$

จากนั้นเราวาดเซกเตอร์เป็นวงกลมตามมุมที่คำนวณโดยใช้ไม้โปรแทรกเตอร์มุม:

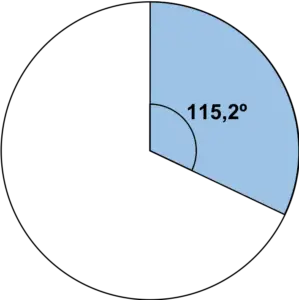
เราทำขั้นตอนเดียวกันซ้ำกับทุกค่า:

$\alpha_{Paris}=12 \cdot \cfrac{360^o}{50}=86,4^o$

$\alpha_{Nueva \ York}=9\cdot \cfrac{360^o}{50}=64,8^o$

$\alpha_{Roma}= 7 \cdot \cfrac{360^o}{50} = 50,4^o$

$\alpha_{Otras}=6 \cdot \cfrac{360^o}{50} = 43,2^o$

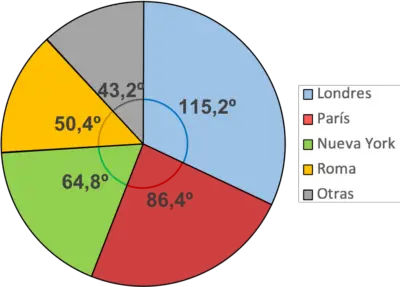
ขอแนะนำให้ทาสีแต่ละส่วนด้วยสีที่แตกต่างกันเพื่อให้แยกแยะได้ง่ายขึ้น ในทำนองเดียวกัน ควรเพิ่มคำอธิบายเพื่อระบุความหมายของแต่ละสี

เมื่อแสดงทุกภาคส่วนแล้ว จำเป็นต้องคำนวณเปอร์เซ็นต์ที่สอดคล้องกับแต่ละภาคส่วน เมื่อต้องการทำเช่นนี้ เราใช้สูตรต่อไปนี้:

$\%_i = f_i \cdot \cfrac{100}{N}$

ทอง

$\%_i$

คือเปอร์เซ็นต์ของแต่ละภาคส่วน

$f_i$

ความถี่และ

$N$

จำนวนข้อมูลทั้งหมดในการศึกษาทางสถิติ

เปอร์เซ็นต์ของแต่ละภาคจึงเป็น:

$\%_{Londres} \cdot \cfrac{100}{N}=16\cdot \cfrac{100}{50}=32\%$

$\%_{Paris}=12 \cdot \cfrac{100}{50}=24\%$

$\%_{Nueva \ York}}=9\cdot\cfrac{100}{50}=18\%$

$\%_{Roma}}=7\cdot\cfrac{100}{50}=14\%$

$\%_{Otras}=6\cdot\cfrac{100}{50}=12\%$

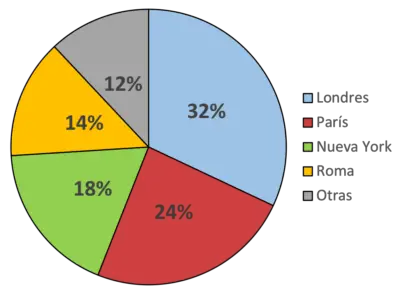
จากแผนภาพนี้ เราระบุว่า ตัวอย่างเช่น สีฟ้าแสดงถึงเมืองลอนดอน ซึ่งเป็นเมืองที่คนส่วนใหญ่ชื่นชอบ (32% ของผู้คน) ในทำนองเดียวกัน สีเขียวแสดงถึงนิวยอร์ก ซึ่งเป็นเมืองโปรดของผู้ตอบแบบสอบถาม 18%

ข้อดีและข้อเสียของแผนภูมิวงกลม

เนื่องจากคุณลักษณะเฉพาะ แผนภูมิวงกลมจึงมีข้อดีและข้อเสียดังต่อไปนี้:

ข้อได้เปรียบ:

นี่คือกราฟทางสถิติที่มีภาพชัดเจนซึ่งช่วยให้คุณวิเคราะห์และสรุปผลได้อย่างรวดเร็ว
มันมีประโยชน์มากสำหรับการสร้างกราฟข้อมูลเชิงคุณภาพ
หากทำด้วยคอมพิวเตอร์ เช่น Excel จะทำได้อย่างรวดเร็วมาก

ข้อเสีย:

เมื่อมีส่วนต่างๆ มากมายบนแผนภูมิ การอ่านแผนภูมิอาจมีความซับซ้อน ในกรณีนี้ ขอแนะนำให้จัดกลุ่มเซกเตอร์ขนาดเล็กเป็นเซกเตอร์เดียวที่เรียกว่า “อื่นๆ”
มีแผนภาพทางสถิติประเภทอื่นๆ ที่เหมาะสมกว่าในการแสดงตัวแปรเชิงปริมาณหรืออนุกรมเวลา

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม

แผนภูมิวงกลมคืออะไร?

วิธีทำแผนภูมิวงกลม

ตัวอย่างแผนภูมิวงกลม

ข้อดีและข้อเสียของแผนภูมิวงกลม

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

เพิ่มความคิดเห็น