แฟกทอเรียล anova คืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

การวิเคราะห์ความแปรปรวนแบบแฟคทอเรียล คือการวิเคราะห์ความแปรปรวนใดๆ (“การวิเคราะห์ความแปรปรวน”) ที่ใช้ปัจจัยอิสระตั้งแต่ 2 ตัวขึ้นไปและตัวแปรตอบสนองตัวเดียว

ANOVA ประเภทนี้ควรใช้เมื่อใดก็ตามที่คุณต้องการทำความเข้าใจว่าปัจจัยตั้งแต่ 2 ตัวขึ้นไปส่งผลต่อ ตัวแปรการตอบสนอง อย่างไร และจะมีผลกระทบต่อการโต้ตอบระหว่างปัจจัยในตัวแปรตอบสนองหรือไม่

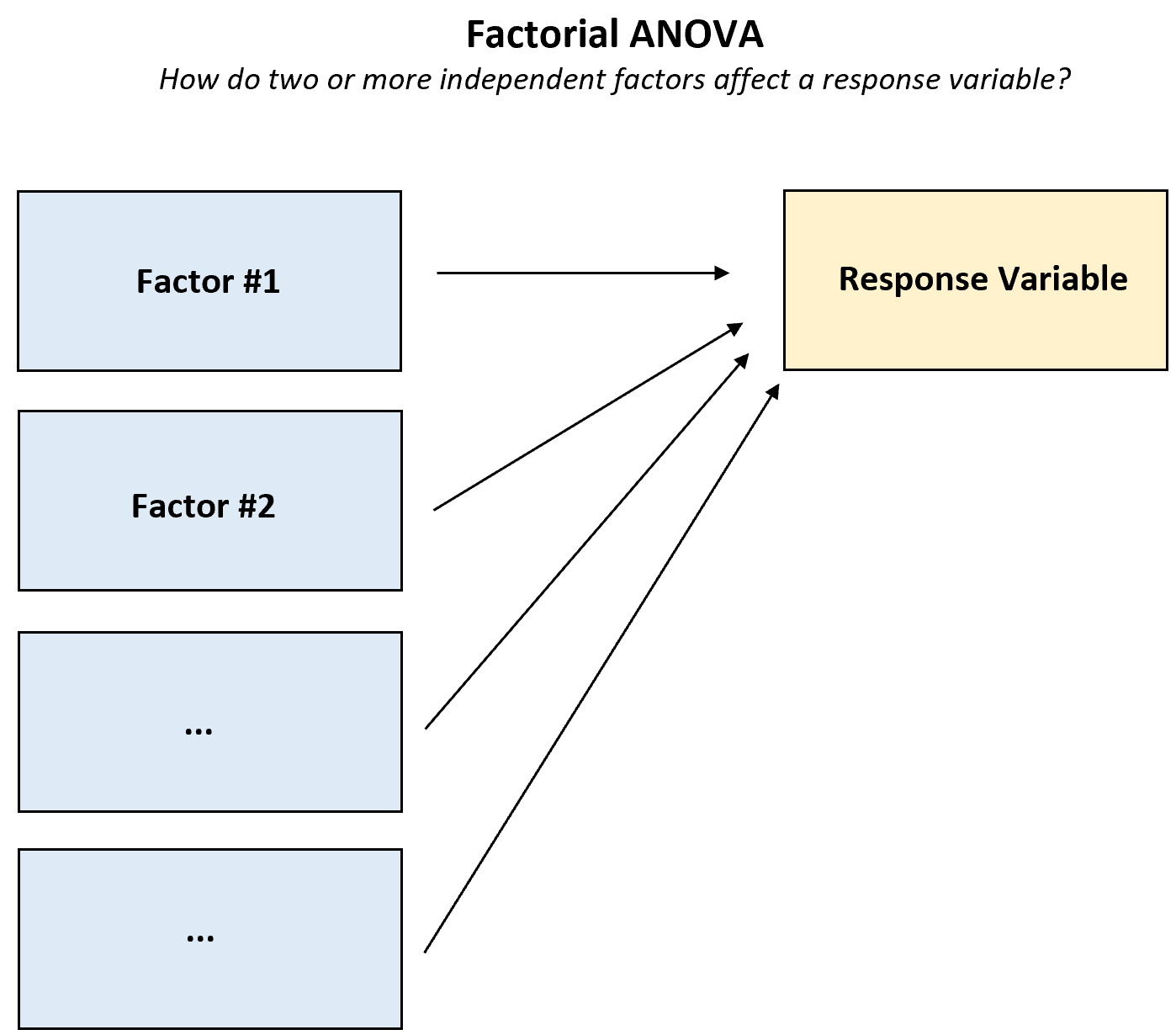
บทช่วยสอนนี้มีตัวอย่างสถานการณ์ต่างๆ มากมายที่สามารถใช้ Factorial ANOVA ได้ รวมถึงตัวอย่างวิธีดำเนินการ ANOVA แบบแฟคทอเรียลแบบทีละขั้นตอน

หมายเหตุ: การวิเคราะห์ความแปรปรวนแบบสองทาง คือการวิเคราะห์ความแปรปรวนแบบแฟคทอเรียลประเภทหนึ่ง

ตัวอย่างการใช้แฟคทอเรียล ANOVA

Factorial ANOVA สามารถใช้ในแต่ละสถานการณ์ต่อไปนี้

ตัวอย่างที่ 1: การเจริญเติบโตของพืช

นักพฤกษศาสตร์ต้องการทำความเข้าใจว่าแสงแดดและความถี่ในการรดน้ำส่งผลต่อการเจริญเติบโตของพืชอย่างไร เธอปลูกเมล็ดพืช 100 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาสามเดือนภายใต้สภาวะแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน หลังจากผ่านไปสามเดือน เธอก็บันทึกความสูงของต้นไม้แต่ละต้น

ในกรณีนี้จะมีตัวแปรดังต่อไปนี้:

• ตัวแปรตอบสนอง: การเจริญเติบโตของพืช
• ปัจจัย: แสงแดด, ความถี่ในการรดน้ำ

และเธอต้องการตอบคำถามต่อไปนี้:

• แสงแดดส่งผลต่อการเจริญเติบโตของพืชหรือไม่?
• ความถี่ในการรดน้ำส่งผลต่อการเจริญเติบโตของพืชหรือไม่?
• มีผลกระทบต่อปฏิสัมพันธ์ระหว่างแสงแดดและความถี่ในการรดน้ำหรือไม่?

เธออาจใช้การวิเคราะห์ความแปรปรวนแบบแฟคทอเรียลสำหรับการวิเคราะห์นี้ เนื่องจากเธอต้องการเข้าใจว่าปัจจัย 2 ประการส่งผลต่อตัวแปรตอบสนองตัวเดียวอย่างไร

ตัวอย่างที่ 2: ผลการสอบ

อาจารย์ต้องการเข้าใจว่าเวลาเรียนและวิธีการสอนส่งผลต่อผลการสอบอย่างไร โดยใช้วิธีการสอนที่แตกต่างกันสองวิธีและสองเวลาสอนที่แตกต่างกัน (ช่วงเช้าตรู่และช่วงบ่าย) และบันทึกคะแนนสอบเฉลี่ยของนักเรียนแต่ละคนเมื่อสิ้นสุดภาคการศึกษา

ในกรณีนี้จะมีตัวแปรดังนี้:

• ตัวแปรตอบสนอง: คะแนนสอบ
• ปัจจัย: วิธีการสอน เวลาสอน

และเขาอยากจะตอบคำถามต่อไปนี้:

• วิธีการสอนส่งผลต่อผลการสอบหรือไม่?
• เวลาสอนส่งผลต่อคะแนนสอบหรือไม่?
• มีผลกระทบต่อปฏิสัมพันธ์ระหว่างวิธีการสอนและเวลาสอนหรือไม่?

เขาอาจใช้การวิเคราะห์ความแปรปรวนแบบแฟคทอเรียลสำหรับการวิเคราะห์นี้ เพราะเขาต้องการเข้าใจว่าปัจจัย 2 ประการส่งผลต่อตัวแปรตอบสนองตัวเดียวอย่างไร

ตัวอย่างที่ 3: รายได้ต่อปี

นักเศรษฐศาสตร์รวบรวมข้อมูลเพื่อทำความเข้าใจว่าระดับการศึกษา (ประกาศนียบัตรมัธยมปลาย ประกาศนียบัตรวิทยาลัย ปริญญาบัณฑิต) สถานภาพการสมรส (โสด หย่าร้าง แต่งงานแล้ว) และภูมิภาค (เหนือ ตะวันออก ใต้ ตะวันตก) ส่งผลต่อรายได้ต่อปีอย่างไร

ในกรณีนี้จะมีตัวแปรดังนี้:

• ตัวแปรตอบสนอง: รายได้ต่อปี
• ปัจจัย: ระดับการศึกษา สถานภาพสมรส ภูมิภาค

และเขาอยากจะตอบคำถามต่อไปนี้:

• ระดับการศึกษาส่งผลต่อรายได้หรือไม่?
• สถานภาพการสมรสส่งผลต่อรายได้หรือไม่?
• ภูมิภาคส่งผลต่อรายได้หรือไม่?
• มีผลกระทบปฏิสัมพันธ์ระหว่างปัจจัยอิสระทั้งสามนี้หรือไม่?

เขาอาจใช้การวิเคราะห์ความแปรปรวนแบบแฟคทอเรียลสำหรับการวิเคราะห์นี้ เพราะเขาต้องการเข้าใจว่าปัจจัย 3 ประการส่งผลต่อตัวแปรตอบสนองตัวเดียวอย่างไร

ตัวอย่างแฟคทอเรียล ANOVA ทีละขั้นตอน

นักพฤกษศาสตร์ต้องการทราบว่าการได้รับแสงแดดและความถี่ในการรดน้ำส่งผลต่อการเจริญเติบโตของพืชหรือไม่ เธอปลูกเมล็ดพืช 40 เมล็ดและปล่อยให้มันเติบโตเป็นเวลาสองเดือนในสภาพแสงแดดและความถี่ในการรดน้ำที่แตกต่างกัน หลังจากผ่านไปสองเดือน เธอก็บันทึกความสูงของต้นไม้แต่ละต้น

ผลลัพธ์แสดงไว้ด้านล่าง:

เราจะเห็นได้ว่ามีการปลูกพืชห้าต้นในแต่ละสภาวะรวมกัน

ตัวอย่างเช่น ปลูกต้นไม้ 5 ต้นโดยรดน้ำทุกวันและไม่มีแสงแดด และความสูงหลังจากสองเดือนคือ 4.8 นิ้ว 4.4 นิ้ว 3.2 นิ้ว 3.9 นิ้ว และ 4.4 นิ้ว:

นักพฤกษศาสตร์ใช้ข้อมูลนี้เพื่อทำการวิเคราะห์ ความแปรปรวนแบบแฟคทอเรียลใน Excel และรับผลลัพธ์ต่อไปนี้:

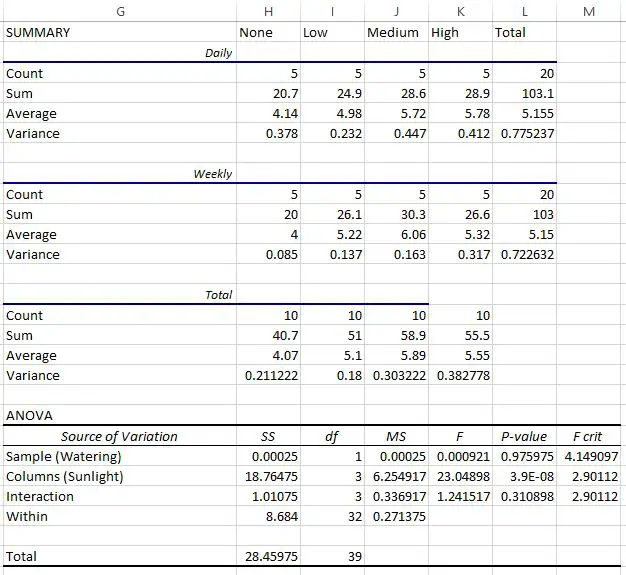
ตารางสุดท้ายแสดงผลลัพธ์ของแฟคทอเรียล ANOVA:

• ค่า p ของปฏิสัมพันธ์ระหว่างความถี่ในการรดน้ำและแสงแดดเท่ากับ 0.310898 ซึ่งไม่มีนัยสำคัญทางสถิติที่ระดับอัลฟ่า 0.05
• ค่า p ความถี่ในการรดน้ำเท่ากับ 0.975975 ซึ่งไม่มีนัยสำคัญทางสถิติที่ระดับอัลฟ่า 0.05
• ค่า p ของการรับแสงแดดคือ 3.9E-8 (0.000000039) ซึ่งมีนัยสำคัญทางสถิติที่ระดับอัลฟา 0.05

เราสามารถสรุปได้ว่าการได้รับแสงแดดเป็นปัจจัยเดียวที่มีผลกระทบที่มีนัยสำคัญทางสถิติต่อการเจริญเติบโตของพืช

นอกจากนี้เรายังสามารถสรุปได้ว่าไม่มีผลกระทบต่อปฏิสัมพันธ์ระหว่างแสงแดดกับความถี่ในการรดน้ำ และความถี่ในการรดน้ำไม่มีผลกระทบที่มีนัยสำคัญทางสถิติต่อการเจริญเติบโตของพืช พืช.

แหล่งข้อมูลเพิ่มเติม

บทช่วยสอนต่อไปนี้ให้ข้อมูลเพิ่มเติมเกี่ยวกับแบบจำลอง ANOVA:

ข้อมูลเบื้องต้นเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบทางเดียว
ข้อมูลเบื้องต้นเกี่ยวกับการวิเคราะห์ความแปรปรวนแบบสองทาง
ข้อมูลเบื้องต้นเกี่ยวกับ ANOVA การวัดซ้ำ
ความแตกต่างระหว่าง ANOVA, ANCOVA, MANOVA และ MANCOVA