แบบทดสอบแมนน์-วิทนีย์ ยู
การทดสอบ Mann-Whitney U (บางครั้งเรียกว่าการทดสอบผลรวมอันดับของ Wilcoxon) ใช้เพื่อเปรียบเทียบความแตกต่างระหว่างตัวอย่างอิสระ 2 ตัวอย่าง เมื่อการแจกแจงตัวอย่างไม่กระจายตามปกติและขนาดตัวอย่างมีขนาดเล็ก (n < 30)
ถือว่าเทียบเท่าแบบไม่มีพารามิเตอร์ของ การทดสอบ t สองตัวอย่างอิสระ
นี่คือตัวอย่างบางส่วนของเวลาที่คุณสามารถใช้การทดสอบ Mann-Whitney U:
- คุณต้องการเปรียบเทียบเงินเดือนของผู้สำเร็จการศึกษาห้าคนจากมหาวิทยาลัย A กับเงินเดือนของผู้สำเร็จการศึกษาห้าคนจากมหาวิทยาลัย B โดยปกติแล้วระบบจะไม่กระจายเงินเดือน
- คุณต้องการทราบว่าการลดน้ำหนักแตกต่างกันไปสำหรับสองกลุ่มหรือไม่: 12 คนที่ใช้อาหาร A และ 10 คนที่ใช้อาหาร B โดยน้ำหนักที่ลดลงนั้นไม่มีการกระจายตามปกติ
- คุณต้องการทราบว่าคะแนนของนักเรียน 8 คนในชั้นเรียน A แตกต่างจากนักเรียน 7 คนในชั้นเรียน B หรือไม่ โดยทั่วไปคะแนนจะไม่กระจาย
ในแต่ละตัวอย่าง คุณต้องการเปรียบเทียบสองกลุ่ม การแจกแจงการสุ่มตัวอย่างไม่ปกติ และขนาดตัวอย่างมีขนาดเล็ก
ดังนั้นการทดสอบ Mann-Whitney U จึงเหมาะสมตราบใดที่เป็นไปตามสมมติฐานต่อไปนี้
สมมติฐานการทดสอบ Mann-Whitney U
ก่อนที่จะทำการทดสอบ Mann-Whitney U คุณต้องแน่ใจว่าเป็นไปตามสมมติฐานสี่ประการต่อไปนี้:
- สามัญหรือต่อเนื่อง: ตัวแปรที่คุณกำลังวิเคราะห์นั้นเป็นลำดับหรือต่อเนื่อง ตัวอย่างของตัวแปรลำดับ ได้แก่ รายการ Likert (เช่น ระดับคะแนน 5 คะแนนตั้งแต่ “ไม่เห็นด้วยอย่างยิ่ง” ไปจนถึง “เห็นด้วยอย่างยิ่ง”) ตัวอย่างของตัวแปรต่อเนื่อง ได้แก่ ส่วนสูง (วัดเป็นนิ้ว) น้ำหนัก (วัดเป็นปอนด์) หรือคะแนนการทดสอบ (วัดตั้งแต่ 0 ถึง 100)
- ความเป็นอิสระ: การสังเกตทั้งหมดจากทั้งสองกลุ่มมีความเป็นอิสระจากกัน
- รูปร่าง: รูปร่างของการแจกแจงของทั้งสองกลุ่มจะใกล้เคียงกัน
หากเป็นไปตามสมมติฐานเหล่านี้ คุณสามารถทำการทดสอบ Mann-Whitney U ได้
วิธีทำแบบทดสอบ Mann-Whitney U
ในการทำการทดสอบ Mann-Whitney U เราจะปฏิบัติตาม ขั้นตอนการทดสอบสมมติฐานห้าขั้นตอนมาตรฐาน :
1. ระบุสมมติฐาน
ในกรณีส่วนใหญ่ การทดสอบ Mann-Whitney U จะดำเนินการเป็นการทดสอบแบบสองด้าน สมมติฐานว่างและทางเลือกเขียนอยู่ในรูปแบบ:
H 0 : ประชากรทั้งสองมีค่าเท่ากัน
H a : ประชากรทั้งสองไม่เท่ากัน
2. กำหนดระดับนัยสำคัญเพื่อใช้ตั้งสมมติฐาน
ตัดสินใจเลือกระดับความสำคัญ ตัวเลือกทั่วไปคือ .01, .05 และ .1
3. ค้นหาสถิติการทดสอบ
สถิติการทดสอบแสดงโดย U และมีค่าน้อยกว่า U 1 และ U 2 ตามที่กำหนดด้านล่าง:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
โดยที่ n 1 และ n 2 คือขนาดตัวอย่างสำหรับตัวอย่างที่ 1 และ 2 ตามลำดับ และ R 1 และ R 2 คือผลรวมของอันดับสำหรับตัวอย่างที่ 1 และ 2 ตามลำดับ
ตัวอย่างด้านล่างจะแสดงวิธีค้นหาสถิติการทดสอบนี้โดยละเอียด
4. ปฏิเสธหรือไม่ปฏิเสธสมมติฐานที่เป็นโมฆะ
ใช้สถิติทดสอบ พิจารณาว่าคุณสามารถปฏิเสธสมมติฐานว่างตามระดับนัยสำคัญและค่าวิกฤตที่พบในตาราง Mann-Whitney U ได้หรือไม่
5. ตีความผลลัพธ์
ตีความผลการทดสอบตามบริบทของคำถามที่ถาม
ตัวอย่างการทำแบบทดสอบ Mann-Whitney U
ตัวอย่างต่อไปนี้แสดงวิธีดำเนินการทดสอบ Mann-Whitney U
ตัวอย่างที่ 1
เราต้องการทราบว่ายาตัวใหม่มีประสิทธิภาพในการป้องกันการโจมตีเสียขวัญหรือไม่ ผู้ป่วยทั้งหมด 12 ราย สุ่มแบ่งเป็น 2 กลุ่ม กลุ่มละ 6 ราย และกำหนดให้รับยาใหม่หรือยาหลอก จากนั้นผู้ป่วยจะบันทึกจำนวนการโจมตีเสียขวัญที่พวกเขาพบในช่วงหนึ่งเดือน
ผลลัพธ์แสดงไว้ด้านล่าง:
| ยาใหม่ | พลาเซโบ |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
ทำการทดสอบ Mann-Whitney U เพื่อดูว่าจำนวนการโจมตีเสียขวัญในผู้ป่วยที่ได้รับยาหลอกมีความแตกต่างกันหรือไม่เมื่อเทียบกับกลุ่มยาใหม่ ใช้ระดับนัยสำคัญ 0.05
1. ระบุสมมติฐาน
H 0 : ประชากรทั้งสองมีค่าเท่ากัน
H a : ประชากรทั้งสองไม่เท่ากัน
2. กำหนดระดับนัยสำคัญเพื่อใช้ตั้งสมมติฐาน
ปัญหาบอกเราว่าเราควรใช้ระดับนัยสำคัญที่ 0.05
3. ค้นหาสถิติการทดสอบ
โปรดจำไว้ว่าสถิติการทดสอบแสดงเป็น U และมีค่าน้อยกว่า U 1 และ U 2 ตามที่กำหนดไว้ด้านล่าง:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
โดยที่ n 1 และ n 2 คือขนาดตัวอย่างสำหรับตัวอย่างที่ 1 และ 2 ตามลำดับ และ R 1 และ R 2 คือผลรวมของอันดับสำหรับตัวอย่างที่ 1 และ 2 ตามลำดับ
ในการค้นหา R 1 และ R 2 เราจำเป็นต้องรวมการสังเกตจากทั้งสองกลุ่มและเรียงลำดับจากเล็กที่สุดไปใหญ่ที่สุด:
| ยาใหม่ | พลาเซโบ |
|---|---|
| 3 | 4 |
| 5 | 8 |
| 1 | 6 |
| 4 | 2 |
| 3 | 1 |
| 5 | 9 |
ตัวอย่างทั้งหมด: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9
อันดับ: 1.5 , 1.5 , 3 , 4.5 , 4.5 , 6.5 , 6.5 , 8.5 , 8.5 , 10 , 11 , 12
R 1 = ผลรวมของอันดับสำหรับตัวอย่าง 1 = 1.5+4.5+4.5+6.5+8.5+8.5 = 34
R 2 = ผลรวมของอันดับสำหรับตัวอย่าง 2 = 1.5+3+6.5+10+11+12 = 44
ต่อไป เราใช้ขนาดตัวอย่าง n 1 และ n 2 เช่นเดียวกับผลรวมอันดับ R 1 และ R 2 เพื่อค้นหา U 1 และ U 2
U1 = 6(6) + 6(6+1)/2 – 34 = 23
U2 = 6(6) + 6(6+1)/2 – 44 = 13
สถิติการทดสอบของเรานั้นน้อยกว่า U1 และ U2 ซึ่งก็คือ U=13
หมายเหตุ: เราสามารถใช้ เครื่องคิดเลขทดสอบ Mann-Whitney U เพื่อระบุได้ว่า U = 13
4. ปฏิเสธหรือไม่ปฏิเสธสมมติฐานที่เป็นโมฆะ
การใช้ n 1 = 6 และ n 2 = 6 โดยมีระดับนัยสำคัญเท่ากับ 0.05 ตาราง Mann-Whitney U บอกเราว่าค่าวิกฤตคือ 5:
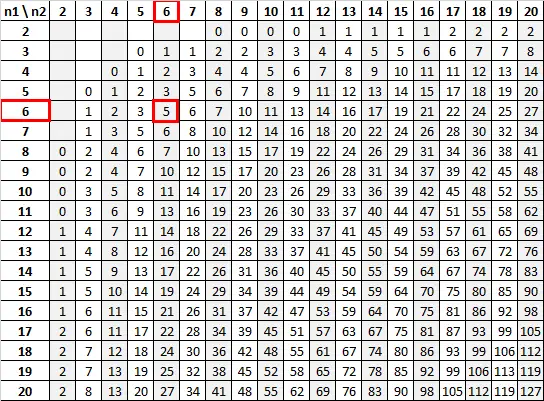
เนื่องจากสถิติการทดสอบของเรา (13) มากกว่าค่าวิกฤตของเรา (5) เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้
5. ตีความผลลัพธ์
เนื่องจากเราไม่สามารถปฏิเสธสมมติฐานว่างได้ เราจึงไม่มีหลักฐานเพียงพอที่จะกล่าวว่าจำนวนการโจมตีเสียขวัญที่ผู้ป่วยในกลุ่มยาหลอกประสบนั้นแตกต่างจากจำนวนในกลุ่มยาใหม่
ตัวอย่างที่ 2
เราต้องการทราบว่าการเรียนวันละ 30 นาทีเป็นเวลาหนึ่งสัปดาห์จะช่วยให้นักเรียนทำข้อสอบได้ดีขึ้นหรือไม่ ผู้ป่วยทั้งหมด 15 รายได้รับการสุ่มให้ทำการศึกษาหรือไม่มีกลุ่มการศึกษา หลังจากผ่านไปหนึ่งสัปดาห์ นักเรียนทุกคนจะทำแบบทดสอบเดียวกัน
ผลการทดสอบสำหรับทั้งสองกลุ่มแสดงไว้ด้านล่าง:
| ศึกษา | ไม่มีการศึกษา |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
ทำแบบทดสอบ Mann-Whitney U เพื่อดูว่าคะแนนการทดสอบของกลุ่มเรียนมีความแตกต่างกับกลุ่มที่ไม่มีการศึกษาหรือไม่ ใช้ระดับนัยสำคัญ 0.01
1. ระบุสมมติฐาน
H 0 : ประชากรทั้งสองมีค่าเท่ากัน
H a : ประชากรทั้งสองไม่เท่ากัน
2. กำหนดระดับนัยสำคัญเพื่อใช้ตั้งสมมติฐาน
ปัญหาบอกเราว่าเราควรใช้ระดับนัยสำคัญที่ 0.01
3. ค้นหาสถิติการทดสอบ
โปรดจำไว้ว่าสถิติการทดสอบแสดงเป็น U และมีค่าน้อยกว่า U 1 และ U 2 ตามที่กำหนดไว้ด้านล่าง:
U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1
U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2
โดยที่ n 1 และ n 2 คือขนาดตัวอย่างสำหรับตัวอย่างที่ 1 และ 2 ตามลำดับ และ R 1 และ R 2 คือผลรวมของอันดับสำหรับตัวอย่างที่ 1 และ 2 ตามลำดับ
ในการค้นหา R 1 และ R 2 เราจำเป็นต้องรวมการสังเกตจากทั้งสองกลุ่มและเรียงลำดับจากเล็กที่สุดไปใหญ่ที่สุด:
| ศึกษา | ไม่มีการศึกษา |
|---|---|
| 89 | 88 |
| 92 | 93 |
| 94 | 95 |
| 96 | 75 |
| 91 | 72 |
| 99 | 80 |
| 84 | 81 |
| 90 |
ตัวอย่างทั้งหมด: 72 , 75 , 80 , 81, 84, 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99
แถว: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15
R 1 = ผลรวมของอันดับสำหรับตัวอย่าง 1 = 5+7+8+9+10+12+14+15 = 80
R 2 = ผลรวมของอันดับสำหรับตัวอย่าง 2 = 1+2+3+4+6+11+13 = 40
ต่อไป เราใช้ขนาดตัวอย่าง n 1 และ n 2 เช่นเดียวกับผลรวมอันดับ R 1 และ R 2 เพื่อค้นหา U 1 และ U 2
U1 = 8(7) + 8(8+1)/2 – 80 = 12
U2 = 8(7) + 7(7+1)/2 – 40 = 44
สถิติการทดสอบของเรานั้นน้อยกว่า U1 และ U2 ซึ่งก็คือ U=12
หมายเหตุ: เราสามารถใช้ เครื่องคิดเลขทดสอบ Mann-Whitney U เพื่อระบุได้ว่า U = 12
4. ปฏิเสธหรือไม่ปฏิเสธสมมติฐานที่เป็นโมฆะ
การใช้ n 1 = 8 และ n 2 = 7 โดยมีระดับนัยสำคัญเท่ากับ 0.01 ตาราง Mann-Whitney U บอกเราว่าค่าวิกฤตคือ 6:
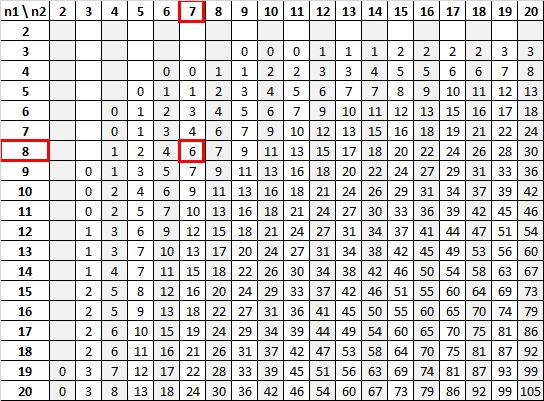
เนื่องจากสถิติการทดสอบของเรา (12) มากกว่าค่าวิกฤตของเรา (6) เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้
5. ตีความผลลัพธ์
เนื่องจากเราไม่สามารถปฏิเสธสมมติฐานว่างได้ เราจึงไม่มีหลักฐานเพียงพอที่จะบอกว่าคะแนนสอบของนักเรียนที่เรียนแตกต่างจากนักเรียนที่ไม่ได้เรียน
แหล่งข้อมูลเพิ่มเติม
เครื่องคิดเลขทดสอบ Mann-Whitney U
ตารางยู แมนน์-วิทนีย์
วิธีดำเนินการทดสอบ Mann-Whitney U ใน Excel
วิธีทำการทดสอบ Mann-Whitney U ใน R
วิธีทำการทดสอบ Mann-Whitney U ใน Python
วิธีดำเนินการทดสอบ Mann-Whitney U ใน SPSS
วิธีทำการทดสอบ Mann-Whitney U ใน Stata