ตัวตนของโมแรนคืออะไร? (คำจำกัดความ & #038; ตัวอย่าง)

Moran’s I เป็นวิธีการวัดความสัมพันธ์อัตโนมัติเชิงพื้นที่

พูดง่ายๆ ก็คือเป็นวิธีหาปริมาณว่าค่าต่างๆ รวมตัวกันอย่างใกล้ชิดในพื้นที่ 2 มิติอย่างไร มักใช้ในภูมิศาสตร์และ วิทยาการสารสนเทศทางภูมิศาสตร์ (GIS) เพื่อวัดว่าคุณลักษณะต่างๆ ที่จัดกลุ่มไว้บนแผนที่มีความใกล้เคียงกันเพียงใด เช่น รายได้ครัวเรือน ระดับการศึกษา เป็นต้น

Moran’s I: สูตร

สูตรคำนวณ I ของ Moran คือ:

I = (N/W)*ΣΣw _ij (x _i – x )(x _j – x )/Σ(x _i – x ) ²

ทอง:

• N: จำนวนหน่วยเชิงพื้นที่ที่ทำดัชนีโดย i และ j
• W: ผลรวมของ _wij ทั้งหมด
• x: ตัวแปรที่น่าสนใจ (รายได้ครัวเรือน ปีการศึกษา ฯลฯ)
• x : ค่าเฉลี่ยของ x
• _wij : เมทริกซ์ของน้ำหนักเชิงพื้นที่

คุณอาจไม่ต้องคำนวณการวัดนี้ด้วยมือเลย เนื่องจากซอฟต์แวร์ทางสถิติส่วนใหญ่สามารถคำนวณให้คุณได้ แต่การทราบสูตรที่ใช้โดยทั่วไปจะช่วยให้คุณทราบสูตรนี้ได้ดียิ่งขึ้น

ค่าของ Moran’s I สามารถอยู่ในช่วงตั้งแต่ -1 ถึง 1 โดยที่:

• -1: ตัวแปรที่สนใจกระจายตัวอย่างสมบูรณ์
• 0: ตัวแปรที่สนใจจะกระจายแบบสุ่ม
• 1: ตัวแปรที่สนใจถูกจัดกลุ่มไว้อย่างสมบูรณ์แบบ

นอกจากการคำนวณ I ของโมแรนแล้ว ซอฟต์แวร์ทางสถิติส่วนใหญ่ยังคำนวณค่า p ที่สอดคล้องกัน ซึ่งสามารถใช้เพื่อระบุได้ว่าข้อมูลกระจายแบบสุ่มหรือไม่

การทดสอบโมแรนใช้สมมติฐานว่างและทางเลือกต่อไปนี้:

สมมติฐานว่าง (H ₀ ): ข้อมูลจะกระจายแบบสุ่ม

สมมติฐานทางเลือก ( _HA ) : ข้อมูล ไม่ ได้กระจายแบบสุ่ม กล่าวคือ มันถูกจัดกลุ่มเป็นรูปแบบที่มองเห็นได้

หากค่า p ที่สอดคล้องกับค่า I ของโมแรนต่ำกว่าระดับนัยสำคัญที่กำหนด (เช่น α = 0.05) เราก็สามารถปฏิเสธสมมติฐานว่างและสรุปได้ว่าข้อมูลถูกจัดกลุ่มเชิงพื้นที่ในลักษณะที่ไม่น่าจะจัดกลุ่มเชิงพื้นที่ได้ เกิดขึ้นโดยบังเอิญ

ฉันของโมแรน: ตัวอย่างบางส่วน

ตัวอย่างต่อไปนี้แสดงถึงไพ่ปลอมที่มีค่าต่างกันสำหรับ Moran’s I

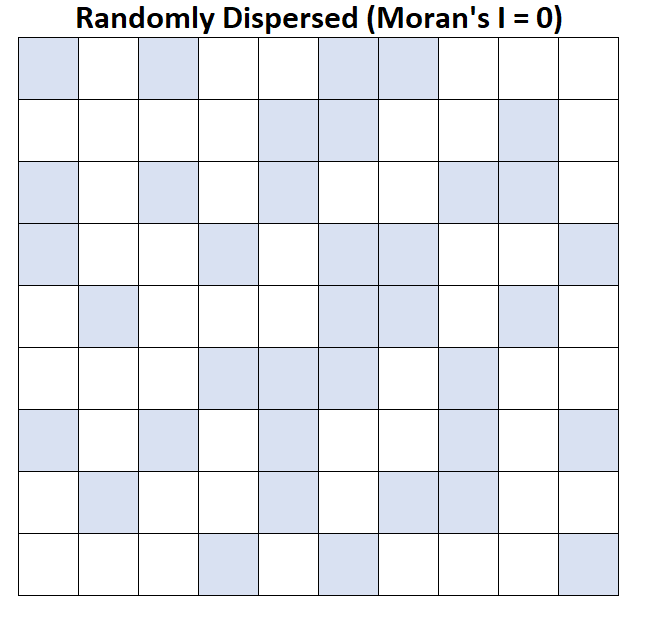
สมมติว่าแต่ละช่องบนแผนที่เป็นตัวแทนของเทศมณฑล และเทศมณฑลที่มีรายได้ครัวเรือนโดยเฉลี่ยมากกว่า 50,000 ดอลลาร์จะแสดงเป็นสีน้ำเงิน

I ของโมแรน = 0: รายได้ครัวเรือนโดยเฉลี่ยจะกระจายแบบสุ่ม (เช่น กระจายเป็นกลุ่มแบบสุ่มในพื้นที่สุ่ม)

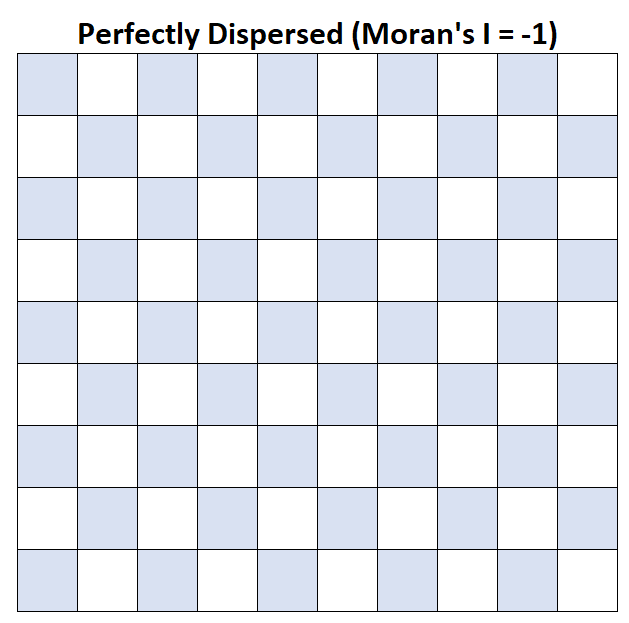
Moran’s I = -1: รายได้ครัวเรือนโดยเฉลี่ยกระจัดกระจายอย่างสมบูรณ์

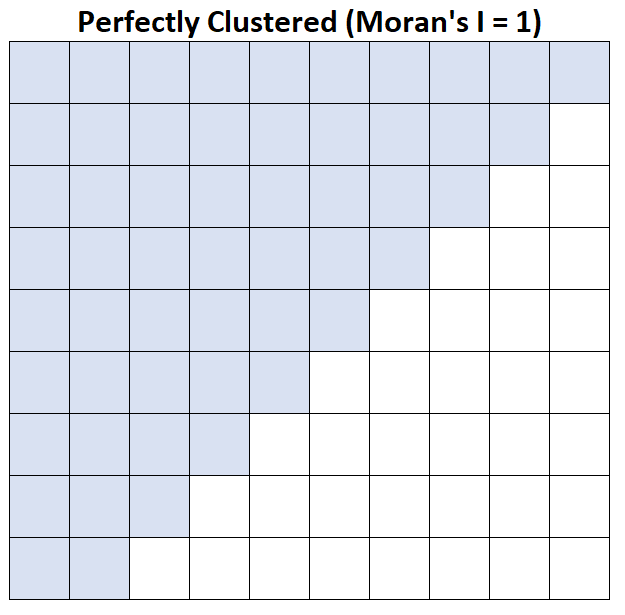
I ของโมแรน = 1: รายได้ครัวเรือนโดยเฉลี่ยถูกจัดกลุ่มไว้อย่างสมบูรณ์แบบ

อ้างถึง ตัวอย่างนี้ สำหรับตัวอย่างที่ชัดเจนของการคำนวณ I ของโมแรนในซอฟต์แวร์ทางสถิติ R