แฟชั่น (สถิติ)

โดย ดร.เบนจามิน แอนเดอร์สัน สิงหาคม 5, 2023 สถิติ 0 ความคิดเห็น

บทความนี้จะอธิบายว่าโหมดใดในสถิติ คุณจะได้เรียนรู้วิธีค้นหาโหมดทางสถิติสำหรับข้อมูลที่จัดกลุ่มและข้อมูลที่ไม่ได้จัดกลุ่ม โหมดประเภทต่างๆ และตัวอย่างต่างๆ ของการวัดทางสถิตินี้

โหมดในสถิติคืออะไร?

ในสถิติ โหมดคือค่าในชุดข้อมูลที่มีความถี่สัมบูรณ์สูงสุด กล่าวคือ โหมดคือค่าที่ซ้ำกันมากที่สุดในชุดข้อมูล

ดังนั้น ในการคำนวณโหมดของชุดข้อมูลทางสถิติ เพียงนับจำนวนครั้งที่แต่ละองค์ประกอบข้อมูลปรากฏในตัวอย่าง และข้อมูลที่ซ้ำกันมากที่สุดจะเป็นโหมด

โหมดใช้เพื่อกำหนดการแจกแจงทางสถิติ เนื่องจากค่าที่ซ้ำกันมากที่สุดมักจะอยู่ที่ศูนย์กลางของการแจกแจง

โหมดนี้อาจกล่าวได้ว่าเป็น โหมดทางสถิติ หรือ ค่ากิริยา ช่วย ในทำนองเดียวกัน เมื่อข้อมูลถูกจัดกลุ่มเป็นช่วงเวลา ช่วงเวลาที่เกิดซ้ำมากที่สุดคือ ช่วงโมดอล หรือ คลาสโมดอล

โดยทั่วไป คำว่า Mo ถูกใช้เป็นสัญลักษณ์สำหรับโหมดทางสถิติ ตัวอย่างเช่น โหมดการกระจาย X คือ Mo(X)

โปรดทราบว่าโหมดเป็นการวัดทางสถิติของตำแหน่งกึ่งกลาง เช่นเดียวกับค่ามัธยฐานและค่าเฉลี่ย ด้านล่างนี้เราจะดูว่าแต่ละมาตรการทางสถิติเหล่านี้หมายถึงอะไร

ประเภทโหมดในสถิติ

ในสถิติ มีโหมดหลายประเภทซึ่งจำแนกตามจำนวนค่าที่ซ้ำกันมากที่สุด:

โหมด Unimodal : มีเพียงค่าเดียวเท่านั้นที่มีจำนวนการทำซ้ำสูงสุด ตัวอย่างเช่น [1, 4, 2, 4, 5, 3]
โหมด Bimodal : จำนวนการทำซ้ำสูงสุดเกิดขึ้นที่ค่าที่แตกต่างกันสองค่า และค่าทั้งสองจะถูกทำซ้ำในจำนวนครั้งเท่ากัน ตัวอย่างเช่น [2, 6, 7, 2, 3, 6, 9]
โหมดมัลติโมดัล : ค่าตั้งแต่สามค่าขึ้นไปมีจำนวนการทำซ้ำสูงสุดเท่ากัน ตัวอย่างเช่น [3, 3, 4, 1, 3, 4, 2, 1, 4, 5, 2, 1]

วิธีค้นหาโหมดทางสถิติ

หากต้องการค้นหาโหมดทางสถิติของชุดข้อมูล คุณต้องทำตามขั้นตอนต่อไปนี้:

ลงข้อมูลให้เป็นระเบียบ ขั้นตอนนี้ไม่บังคับ แต่จะทำให้การนับเลขง่ายขึ้น
นับจำนวนครั้งที่แต่ละตัวเลขปรากฏ
ตัวเลขที่ปรากฏบ่อยที่สุดคือโหมดสถิติ

ตัวอย่างของโหมดทางสถิติ

เมื่อพิจารณาถึงคำจำกัดความของแฟชั่นในสถิติแล้ว ด้านล่างนี้คุณจะเห็นตัวอย่างแฟชั่นแต่ละประเภทเพื่อให้คุณเข้าใจแนวคิดได้ดีขึ้น

ตัวอย่างของโหมดยูนิโมดัล

โหมดของชุดข้อมูลต่อไปนี้คืออะไร?

$5 \ 4 \ 9 \ 7 \ 2 \ 3 \ 9 \ 6 \ 5 \ 2 \ 5$

หมายเลขไม่ได้เรียงลำดับดังนั้นเราจะเรียงลำดับก่อนเพื่อให้ค้นหาโหมดได้ง่ายขึ้น

$2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 7 \ 9 \ 9$

ตัวเลข 2 และ 9 ปรากฏสองครั้ง แต่เลข 5 ซ้ำสามครั้ง ดังนั้นโหมดของชุดข้อมูลจึงเป็นหมายเลข 5

$Mo=5$

ตัวอย่างของโหมดไบโมดัล

คำนวณโหมดของชุดข้อมูลต่อไปนี้:

$8 \ 7 \ 0 \ 6 \ 10 \ 9 \ 13 \ 8 \ 0 \ 6 \ 2 \ 6 \ 5 \ 11 \ 10$

$0 \ 9 \ 8 \ 6 \ 12 \ 3 \ 5 \ 11 \ 1 \ 4 \ 8 \ 10 \ 2 \ 5 \ 7$

ขั้นแรกเราเรียงลำดับตัวเลข:

$0 \ 0 \ 0 \ 1 \ 2 \ 2 \ 3 \ 4 \ 5 \ 5 \ 5 \ 6 \ 6 \ 6 \ 6$

$7 \ 7 \ 8 \ 8 \ 8 \ 8 \ 9 \ 9 \ 10 \ 10 \ 10 \ 11 \ 11 \ 12 \ 13$

อย่างที่คุณเห็นหมายเลข 6 และหมายเลข 8 ปรากฏทั้งหมดสี่ครั้งซึ่งเป็นจำนวนซ้ำสูงสุด ดังนั้น ในกรณีนี้ จะเป็นโหมด bimodal และตัวเลขสองตัวคือโหมดของชุดข้อมูล:

$Mo=\{ 6 \ ; \ 8\}$

ตัวอย่างโหมดมัลติโมดัล

ค้นหาโหมดชุดข้อมูลต่อไปนี้:

$21 \ 27 \ 32 \ 15 \ 13 \ 20 \ 21 \ 21 \ 25 \ 27 \ 31 \ 30 \ 19 \ 20 \ 16$

$22 \ 19 \ 20 \ 31 \ 18 \ 20 \ 25 \ 26 \ 15 \ 20 \ 31 \ 31 \ 27 \ 16 \ 17$

$31 \ 27 \ 24 \ 23 \ 21 \ 27 \ 29 \ 36 \ 32 \ 30 \ 16 \ 22 \ 15 \ 14 \ 37$

เนื่องจากมีข้อมูลจำนวนมาก เราจึงเรียงลำดับจากน้อยไปหามากก่อนเพื่อให้นับได้ง่ายขึ้น:

$13 \ 14 \ 15\ 15\ 15 \ 16 \ 16 \ 16 \ 17 \ 18 \ 19 \ 19 \ 20 \ 20 \ 20$

$20 \ 20 \ 21 \ 21 \ 21\ 21 \ 22 \ 22 \ 23 \ 24 \ 25 \ 25 \ 26 \ 27 \ 27$

$27 \ 27 \ 27 \ 29 \ 30 \ 30 \ 31 \ 31 \ 31 \ 31 \ 31 \ 32 \ 32 \ 36 \ 37$

หมายเลขที่ซ้ำกันมากที่สุดคือ 20, 27 และ 31 โดยทั้งสามหมายเลขซ้ำกันห้าครั้ง โหมดของตัวอย่างนี้จึงเป็นแบบหลายรูปแบบ

$Mo=\{ 20 \ ; \ 27 \ ; \ 31\}$

เครื่องคิดเลขแฟชั่น

ป้อนข้อมูลจากตัวอย่างทางสถิติลงในเครื่องคิดเลขออนไลน์ต่อไปนี้เพื่อคำนวณโหมด ข้อมูลต้องคั่นด้วยช่องว่างและป้อนโดยใช้จุดเป็นตัวคั่นทศนิยม

โหมดสำหรับข้อมูลที่จัดกลุ่ม

เมื่อเราจัดกลุ่มข้อมูลที่จัดกลุ่มเป็นช่วงๆ เราไม่รู้จริงๆ ว่าข้อมูลแต่ละส่วนถูกทำซ้ำกี่ครั้ง แต่เรารู้เฉพาะความถี่ของแต่ละช่วงเท่านั้น

ดังนั้น ในการคำนวณโหมดของข้อมูลที่จัดกลุ่มตามช่วงเวลา เราต้องใช้สูตรต่อไปนี้ :

$Mo=L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i$

ทอง:

L _i คือขีดจำกัดล่างของช่วงโมดอล (ช่วงความถี่สัมบูรณ์สูงสุด)
f _i คือความถี่สัมบูรณ์ของช่วงโมดอล
f _i-1 คือความถี่สัมบูรณ์ของช่วงเวลาก่อนโมดอล
f _i+1 คือความถี่สัมบูรณ์ของช่วงเวลาหลังโมดอล
A _i คือความกว้างของช่วงโมดอล

ตามตัวอย่าง ด้านล่างคุณได้แก้ไขแบบฝึกหัดที่คำนวณโหมดของข้อมูลที่จัดกลุ่มตามช่วงเวลา:

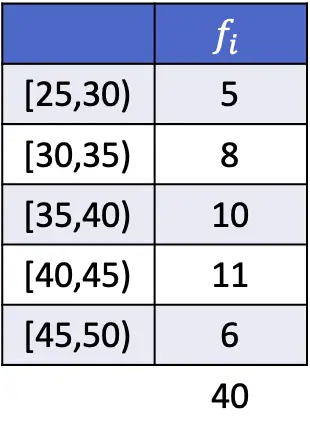
ตัวอย่างโหมดทางสถิติสำหรับข้อมูลที่จัดกลุ่ม

ในกรณีนี้ ช่วงโมดอลคือ [40,45) เนื่องจากเป็นช่วงที่มีความถี่สัมบูรณ์มากที่สุด ดังนั้น พารามิเตอร์สูตรโหมดสำหรับข้อมูลที่จัดกลุ่มคือ:

$\begin{array}{c}L_i=40\\[2ex]f_i=11\\[2ex]f_{i-1}=10\\[2ex]f_{i+1}=6\\[2ex]A_i=5\end{array}$

ดังนั้นเราจึงใช้สูตรเพื่อกำหนดโหมดของข้อมูลที่จัดกลุ่มตามช่วงเวลา และทำการคำนวณ:

$\begin{aligned}Mo & =L_i+ \cfrac{f_i-f_{i-1}}{(f_i-f_{i-1})+(f_i-f_{i+1})}\cdot A_i\\[2ex]& =40+ \cfrac{11-10}{(11-10)+(11-6)}\cdot 5\\[2ex]&=40,83\end{aligned}$

ความแตกต่างระหว่างโหมด ค่าเฉลี่ย และค่ามัธยฐาน

ในส่วนสุดท้ายนี้ เราจะดูว่าอะไรคือความแตกต่างระหว่างโหมด ค่าเฉลี่ย และค่ามัธยฐาน เนื่องจากทั้งสามเป็นการวัดทางสถิติของตำแหน่งศูนย์กลาง ความหมายของมันจึงแตกต่างกัน

ตามที่อธิบายไว้ตลอดบทความ โหมดทางคณิตศาสตร์เป็นค่าที่ซ้ำกันมากที่สุดในชุดข้อมูล

ประการที่สอง ค่าเฉลี่ยคือค่าเฉลี่ยของข้อมูลทางสถิติทั้งหมด ดังนั้น เพื่อให้ได้ค่าเฉลี่ยของข้อมูลบางอย่าง คุณต้องเพิ่มข้อมูลทั้งหมดแล้วหารผลลัพธ์ด้วยจำนวนการสังเกต

และสุดท้าย ค่ามัธยฐานคือค่าที่ครองตำแหน่งศูนย์กลางเมื่อมีการเรียงลำดับข้อมูล

ดังนั้นมาตรการทางสถิติทั้งสามจึงช่วยกำหนดการแจกแจงความน่าจะเป็นเนื่องจากให้แนวคิดเกี่ยวกับค่ากลางของมัน. แต่โปรดจำไว้ว่าไม่มีตัววัดใดที่ดีกว่าตัววัดอื่น พวกเขาแค่หมายถึงแนวคิดที่แตกต่างกัน

คุณสมบัติแฟชั่น

คุณสมบัติของแฟชั่นคือ:

โหมดสามารถพบได้ทั้งในตัวแปรเชิงปริมาณและตัวแปรเชิงคุณภาพ
หากเราใช้การแปลงเชิงเส้นกับตัวแปรสุ่ม ค่าเฉลี่ยจะเปลี่ยนไปตามการดำเนินการที่ใช้

$Mo(X)=Y \ \color{orange}\bm{\longrightarrow}\color{black} \ M(aX+b)=aY+b$

โดยทั่วไป โหมดนี้จะไม่คำนึงถึงค่าผิดปกติ
หากค่าทั้งหมดมีความถี่เท่ากัน แสดงว่าไม่มีโหมด

เกี่ยวกับผู้แต่ง

ดร.เบนจามิน แอนเดอร์สัน

สวัสดี ฉันชื่อเบนจามิน ศาสตราจารย์สถิติเกษียณอายุแล้ว และผันตัวมาเป็นครูสอนสถิติโดยเฉพาะ ด้วยประสบการณ์และความเชี่ยวชาญที่กว้างขวางในสาขาสถิติ ฉันกระตือรือร้นที่จะแบ่งปันความรู้ของฉันเพื่อเสริมศักยภาพนักเรียนผ่าน Statorials. รู้เพิ่มเติม