การทดสอบ chi square fit ใน google ชีต (ทีละขั้นตอน)

การทดสอบความดีพอดีของไคสแควร์ ใช้เพื่อพิจารณาว่าตัวแปรเชิงหมวดหมู่เป็นไปตามการแจกแจงเชิงสมมุติหรือไม่

ตัวอย่างเช่น สมมติว่าเจ้าของร้านอ้างว่ามีลูกค้ามาที่ร้านในจำนวนเท่ากันทุกวันในสัปดาห์

เพื่อทดสอบสมมติฐานนี้ นักวิจัยอิสระจะบันทึกจำนวนลูกค้าที่เข้าร้านในสัปดาห์ที่กำหนดและพบสิ่งต่อไปนี้:

• วันจันทร์: ลูกค้า 50 คน
• วันอังคาร: ลูกค้า 60 คน
• วันพุธ: ลูกค้า 40 คน
• พฤหัสบดี: ลูกค้า 47 คน
• วันศุกร์: ลูกค้า 53 คน

เราสามารถทำการทดสอบความพอดีของไคสแควร์เพื่อตรวจสอบว่าข้อมูลสอดคล้องกับคำกล่าวอ้างของเจ้าของร้านค้าหรือไม่

ตัวอย่างทีละขั้นตอนนี้แสดงวิธีการทดสอบความพอดีของไคสแควร์ใน Google ชีต

ขั้นตอนที่ 1: สร้างข้อมูล

ขั้นแรก ให้ป้อนข้อมูลลงใน Google ชีตในรูปแบบต่อไปนี้:

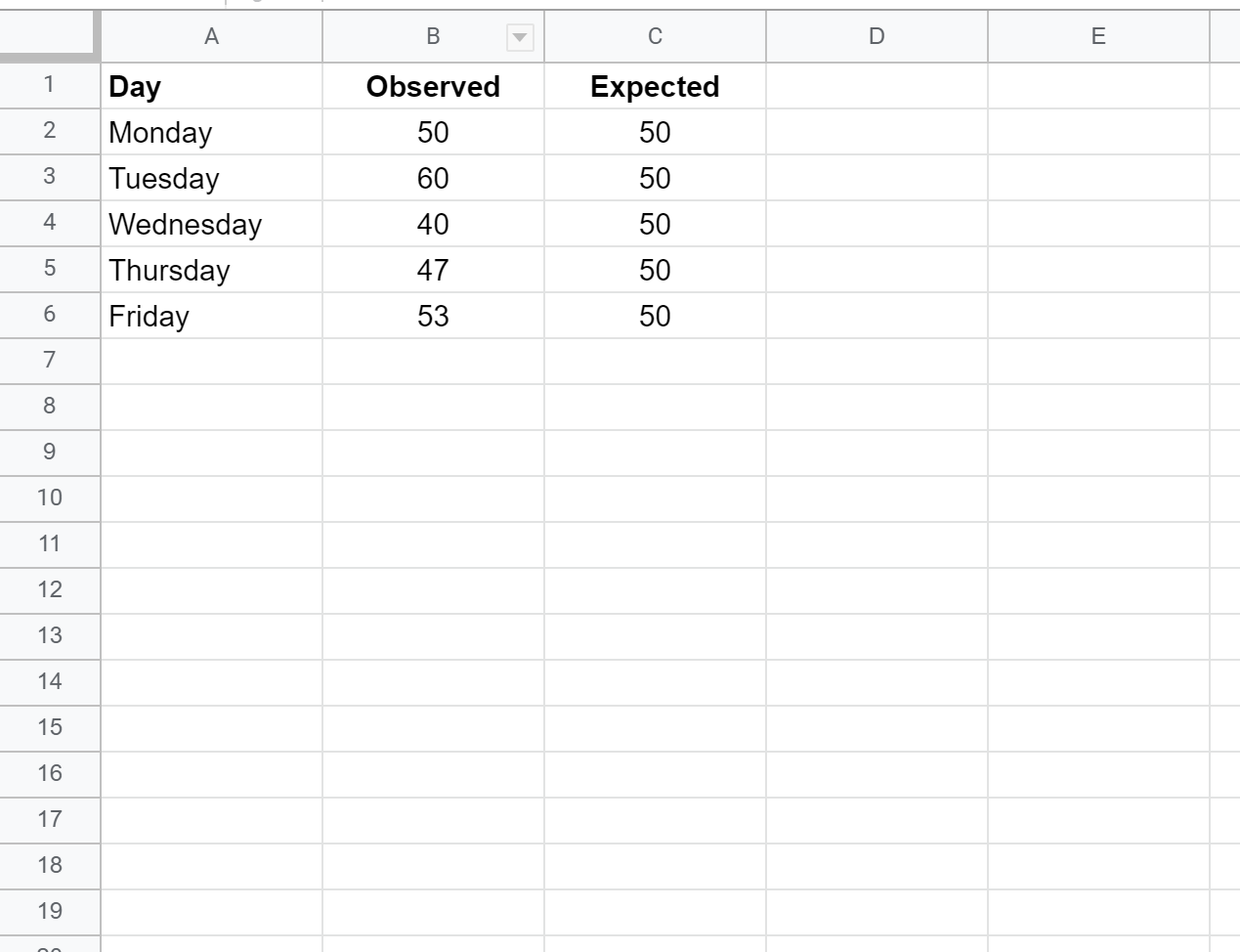
หมายเหตุ: มีลูกค้าทั้งหมด 250 ราย หากเจ้าของร้านคาดหวังว่าจะมีลูกค้าเข้าร้านในจำนวนเท่ากันในแต่ละวัน เขาก็จะคาดหวังว่าจะมีลูกค้า 50 รายต่อวัน

ขั้นตอนที่ 2: คำนวณความแตกต่างระหว่างค่าที่สังเกตได้และค่าที่คาดหวัง

สถิติการทดสอบไคสแควร์สำหรับการทดสอบความดีพอดีคือ X ² = Σ(OE) ² / E

ทอง:

• Σ: เป็นสัญลักษณ์แฟนซีที่หมายถึง “ผลรวม”
• O: ค่าที่สังเกตได้
• E: ค่าที่คาดหวัง

สูตรต่อไปนี้แสดงวิธีคำนวณ (OE) ² /E สำหรับแต่ละแถว:

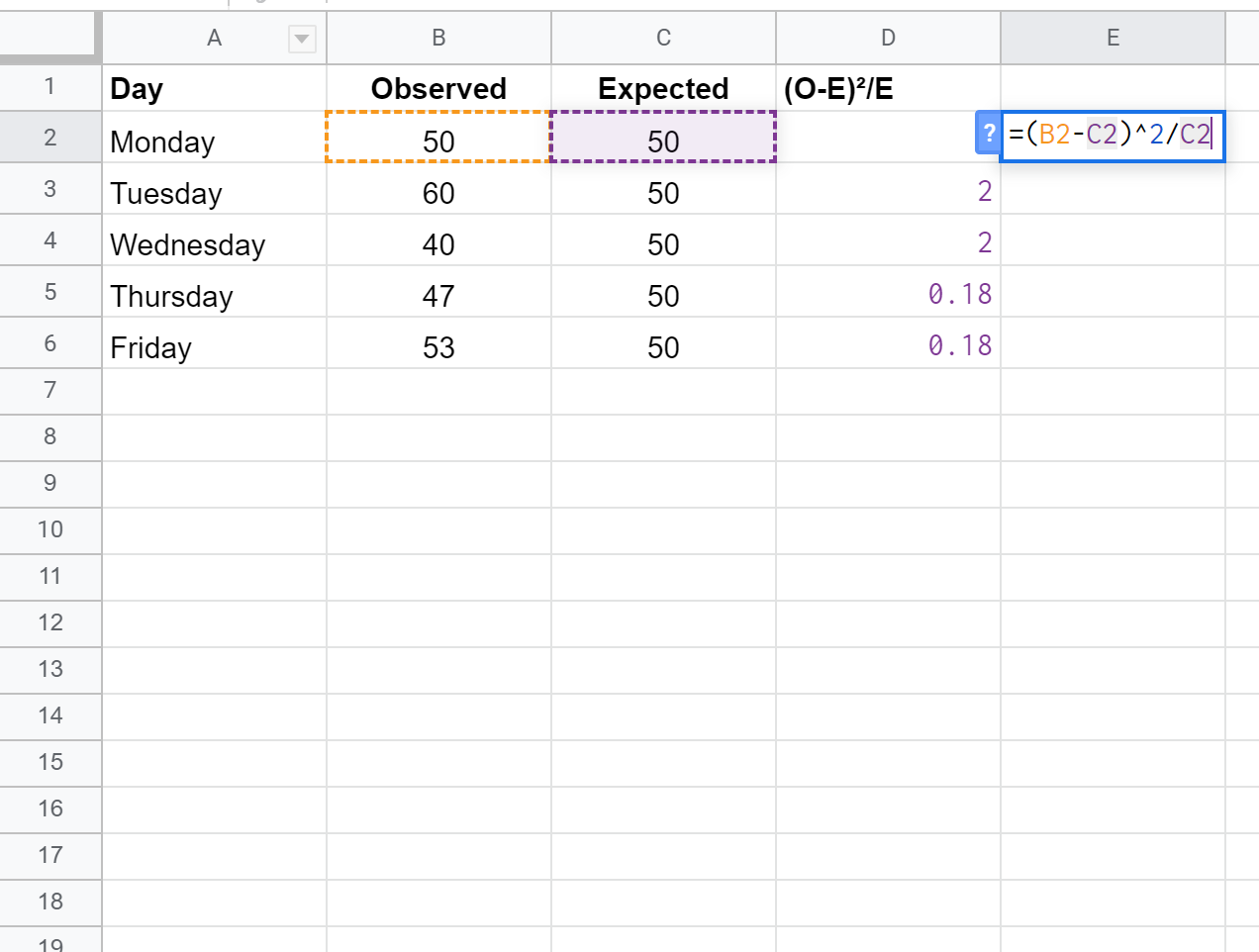
ขั้นตอนที่ 3: คำนวณค่า P

สุดท้ายนี้ เราจะคำนวณสถิติการทดสอบไคสแควร์รวมถึงค่า p ที่สอดคล้องกันโดยใช้สูตรต่อไปนี้:

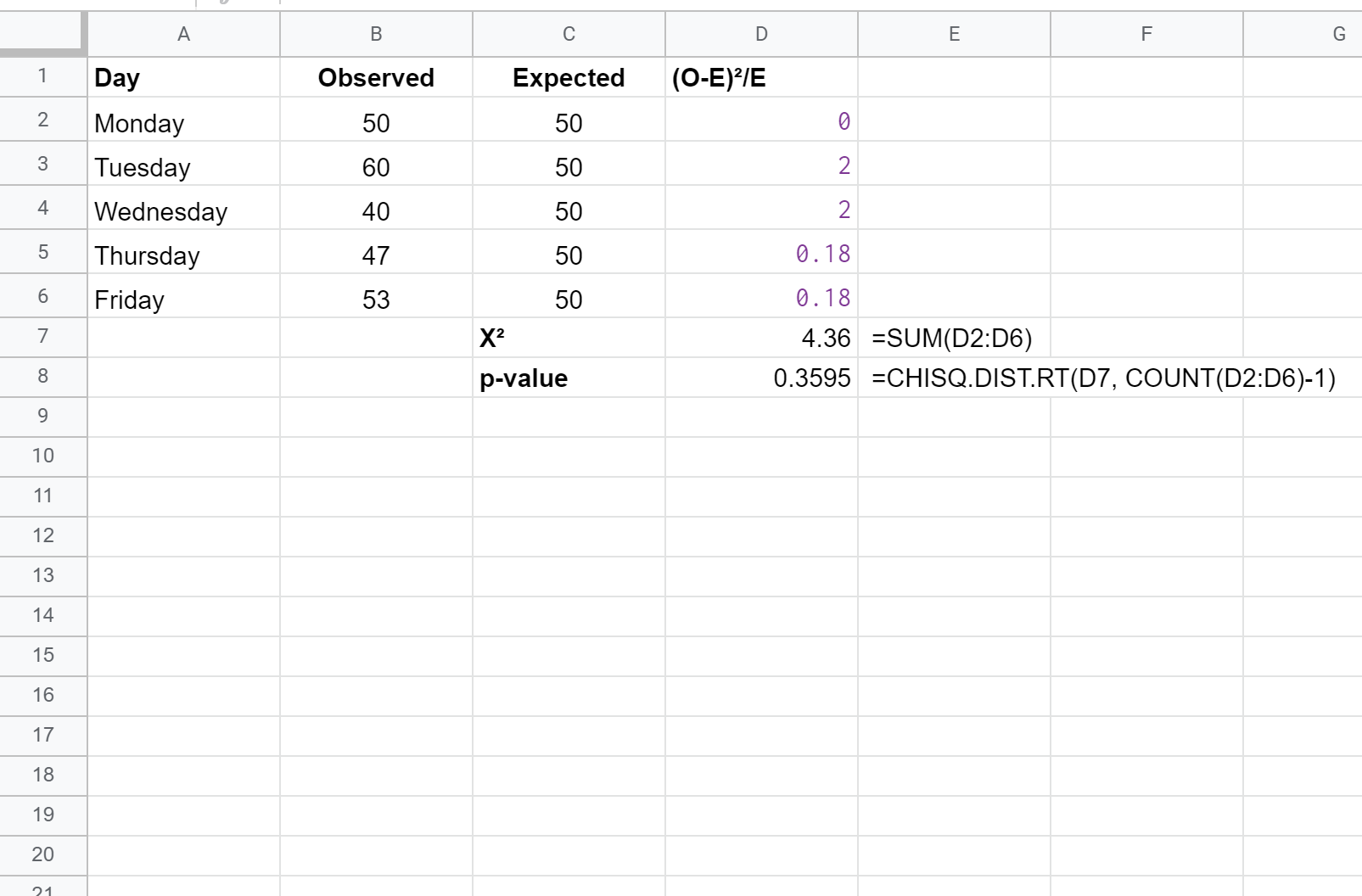
หมายเหตุ: ฟังก์ชัน CHISQ.DIST.RT(x, deg_freedom) จะส่งคืนความน่าจะเป็นที่ถูกต้องของการแจกแจงแบบไคสแควร์ที่เกี่ยวข้องกับสถิติการทดสอบ x และระดับความเป็นอิสระที่แน่นอน องศาความเป็นอิสระคำนวณเป็น n-1 ในกรณีนี้ deg_freedom = 5 – 1 = 4

สถิติการทดสอบ ^X2 สำหรับการทดสอบคือ 4.36 และค่า p ที่สอดคล้องกันคือ 0.3595

เนื่องจากค่า p นี้ไม่น้อยกว่า 0.05 เราจึงไม่สามารถปฏิเสธสมมติฐานว่างได้ ซึ่งหมายความว่าเราไม่มีหลักฐานเพียงพอที่จะบอกว่าการกระจายตัวของลูกค้าที่แท้จริงนั้นแตกต่างจากที่เจ้าของร้านค้ารายงาน

แหล่งข้อมูลเพิ่มเติม

ข้อมูลเบื้องต้นเกี่ยวกับการทดสอบความพอดีของไคสแควร์
เครื่องคำนวณการทดสอบความพอดีของไคสแควร์
คำอธิบายค่า P และนัยสำคัญทางสถิติ