Eksiksiz bir kılavuz: 2×3 faktöriyel tasarım

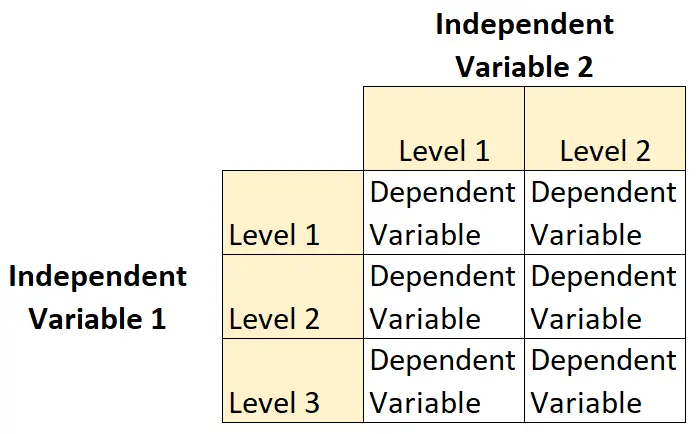
2×3 faktöriyel tasarım, araştırmacıların iki bağımsız değişkenin tek bir bağımlı değişken üzerindeki etkilerini anlamalarına olanak tanıyan bir deney tasarımı türüdür.

Bu tip tasarımda bir bağımsız değişkenin iki düzeyi , diğer bağımsız değişkenin ise üç düzeyi vardır.

Örneğin, bir botanikçinin güneş ışığının (düşük, orta veya yüksek) ve sulama sıklığının (günlük veya haftalık) belirli bir bitki türünün büyümesi üzerindeki etkilerini anlamak istediğini varsayalım.

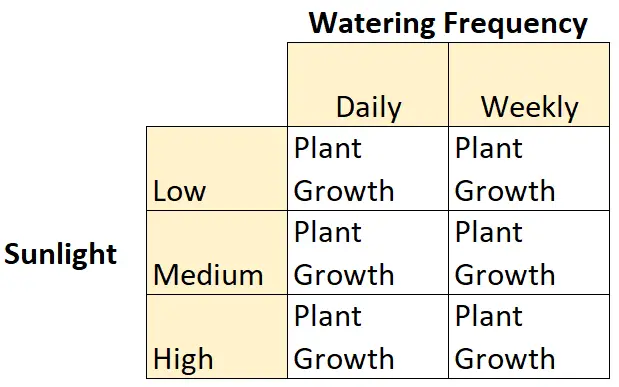
Bu 2 × 3 faktöriyel tasarımın bir örneğidir çünkü biri iki seviyeli ve diğeri üç seviyeli olmak üzere iki bağımsız değişken vardır:

• Bağımsız Değişken #1: Güneş Işığı
  • Seviyeler: Düşük, Orta, Yüksek
• Bağımsız değişken #2: Sulama sıklığı
  • Seviyeler: günlük, haftalık

Bir de bağımlı değişken var: Bitki büyümesi.

2 × 3 faktöriyel tasarımın amacı

2×3 faktöriyel tasarım aşağıdaki etkileri analiz etmenize olanak sağlar:

Ana etkiler: Bunlar, tek bir bağımsız değişkenin bağımlı değişken üzerindeki etkileridir.

Örneğin önceki senaryomuzda aşağıdaki ana etkileri analiz edebiliriz:

• Güneş ışığının bitki büyümesi üzerindeki ana etkisi.
  • Düşük güneş ışığı alan tüm bitkilerin ortalama büyümesi.
  • Ortalama güneş ışığı alan tüm bitkilerin ortalama büyümesi.
  • Yüksek güneş ışığı alan tüm bitkilerin ortalama büyümesi.
• Sulama sıklığının bitki büyümesi üzerindeki temel etkisi.
  • Günlük olarak sulanan tüm bitkilerin ortalama büyümesi.
  • Her hafta sulanan tüm bitkilerin ortalama büyümesi.

Etkileşim etkileri: Bir bağımsız değişkenin bağımlı değişken üzerindeki etkisinin diğer bağımsız değişkenin düzeyine bağlı olması durumunda ortaya çıkar.

Örneğin önceki senaryomuzda aşağıdaki etkileşim etkilerini analiz edebiliriz:

• Güneş ışığının bitki büyümesine etkisi sulama sıklığına bağlı mıdır?
• Sulama sıklığının bitki büyümesine etkisi güneş ışığına bağlı mıdır?

2 × 3 faktöriyel tasarım nasıl analiz edilir

Bağımsız değişkenlerin bağımlı değişkenle istatistiksel olarak anlamlı bir ilişkiye sahip olup olmadığını resmi olarak test etmek için iki yönlü bir ANOVA gerçekleştirebiliriz.

Örneğin aşağıdaki kod, R’deki varsayımsal fabrika senaryomuz için iki yönlü ANOVA’nın nasıl gerçekleştirileceğini gösterir:

 #make this example reproducible
set. seeds (0)

#createdata
df <- data. frame (sunlight = rep(c(' Low ', ' Medium ', ' High '), each = 15, times = 2),
                 water = rep(c(' Daily ', ' Weekly '), each = 45, times = 2),
                 growth = c(rnorm(15, 9, 2), rnorm(15, 10, 3), rnorm(15, 13, 2),
                            rnorm(15, 8, 3), rnorm(15, 10, 4), rnorm(15, 12, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

                Df Sum Sq Mean Sq F value Pr(>F)    
sunlight 2 602.3 301.15 50.811 <2e-16 ***
water 1 39.6 39.62 6.685 0.0105 *  
sunlight:water 2 15.1 7.56 1.275 0.2819    
Residuals 174 1031.3 5.93                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ANOVA sonucunun nasıl yorumlanacağı aşağıda açıklanmıştır:

• Güneş ışığıyla ilişkili p değeri <2e-16’dır . Bu sayının 0,05’ten küçük olması güneş ışığına maruz kalmanın bitki büyümesi üzerinde istatistiksel olarak anlamlı bir etkiye sahip olduğu anlamına gelir.
• Suyla ilgili p değeri 0,0105’tir . Bu rakamın 0,05’ten küçük olması sulama sıklığının da bitki büyümesi üzerinde istatistiksel olarak anlamlı bir etkiye sahip olduğu anlamına gelir.
• Güneş ışığı ile su arasındaki etkileşimin p değeri 0,2819’dur . Bu rakamın 0,05’ten az olmaması güneş ışığı ile su arasında herhangi bir etkileşim etkisinin olmadığı anlamına gelmektedir.

Ek kaynaklar

Aşağıdaki eğitimler deneysel tasarım ve analiz hakkında ek bilgi sağlar:

Eksiksiz bir kılavuz: 2 × 2 faktöriyel tasarım
Bağımsız bir değişkenin seviyeleri nelerdir?
Bağımsız veya bağımlı değişkenler
Faktöriyel ANOVA nedir?