Makine öğreniminde önyargı-varyans değişimi nedir?

Bir modelin veri seti üzerindeki performansını değerlendirmek için modelin tahminlerinin gözlemlenen verilerle ne kadar iyi eşleştiğini ölçmemiz gerekir.

Regresyon modelleri için en yaygın kullanılan ölçüm, aşağıdaki şekilde hesaplanan ortalama karesel hatadır (MSE):

MSE = (1/n)*Σ(y _ben – f(x _ben )) ²

Altın:

• n: toplam gözlem sayısı
• y _i : ^i’inci gözlemin yanıt değeri
• f(x _i ): ^i’inci gözlemin tahmin edilen tepki değeri

Model tahminleri gözlemlere ne kadar yakınsa MSE o kadar düşük olacaktır.

Ancak modelimiz görünmeyen verilere uygulandığında yalnızca MSE testini (MSE) önemsiyoruz. Bunun nedeni, modelin mevcut veriler üzerinde değil, yalnızca bilinmeyen veriler üzerinde nasıl performans göstereceğiyle ilgilenmemizdir.

Örneğin, hisse senedi fiyatlarını tahmin eden bir modelin geçmiş verilerde düşük bir MSE’ye sahip olması sorun değil, ancak modeli gelecekteki verileri doğru bir şekilde tahmin etmek için gerçekten kullanabilmeyi istiyoruz.

MSE testinin hala iki bölüme ayrılabileceği ortaya çıktı:

(1) Varyans: f fonksiyonumuzun farklı bir eğitim seti kullanarak tahmin etmemiz durumunda değişeceği miktarı ifade eder.

(2) Önyargı: Son derece karmaşık olabilecek gerçek bir soruna çok daha basit bir modelle yaklaşılmasının ortaya çıkardığı hatayı ifade eder.

Matematiksel terimlerle yazılmıştır:

MSE testi = Var( f̂( x ₀ )) + [Bias( f̂( x ₀ ))] ² + Var(ε)

MSE testi = Varyans + Sapma ² + İndirgenemez hata

Üçüncü terim olan indirgenemez hata, açıklayıcı değişkenler kümesi ile yanıt değişkeni arasındaki ilişkide her zaman gürültü olması nedeniyle herhangi bir model tarafından azaltılamayan hatadır.

Yüksek yanlılığa sahip modeller düşük varyansa sahip olma eğilimindedir. Örneğin, doğrusal regresyon modelleri yüksek yanlılığa (açıklayıcı değişkenler ile yanıt değişkeni arasında basit bir doğrusal ilişki varsayılarak) ve düşük varyansa (model tahminleri örnekten örneğe çok fazla değişmeyecektir) sahip olma eğilimindedir. diğeri).

Bununla birlikte, düşük yanlılığa sahip modeller yüksek varyansa sahip olma eğilimindedir. Örneğin, karmaşık doğrusal olmayan modeller düşük yanlılığa (açıklayıcı değişkenler ile yanıt değişkeni arasında belirli bir ilişki olduğunu varsaymayın) ve yüksek varyansa (model tahminleri bir öğrenme örneğinden diğerine önemli ölçüde değişebilir) sahip olma eğilimindedir.

Önyargı-varyans değişimi

Önyargı-varyans dengelemesi, genellikle varyansı artıran önyargıyı azaltmayı veya genellikle önyargıyı artıran varyansı azaltmayı seçtiğimizde gerçekleşen dengelemeyi ifade eder.

Aşağıdaki grafik bu ödünleşimi görselleştirmenin bir yolunu sunmaktadır:

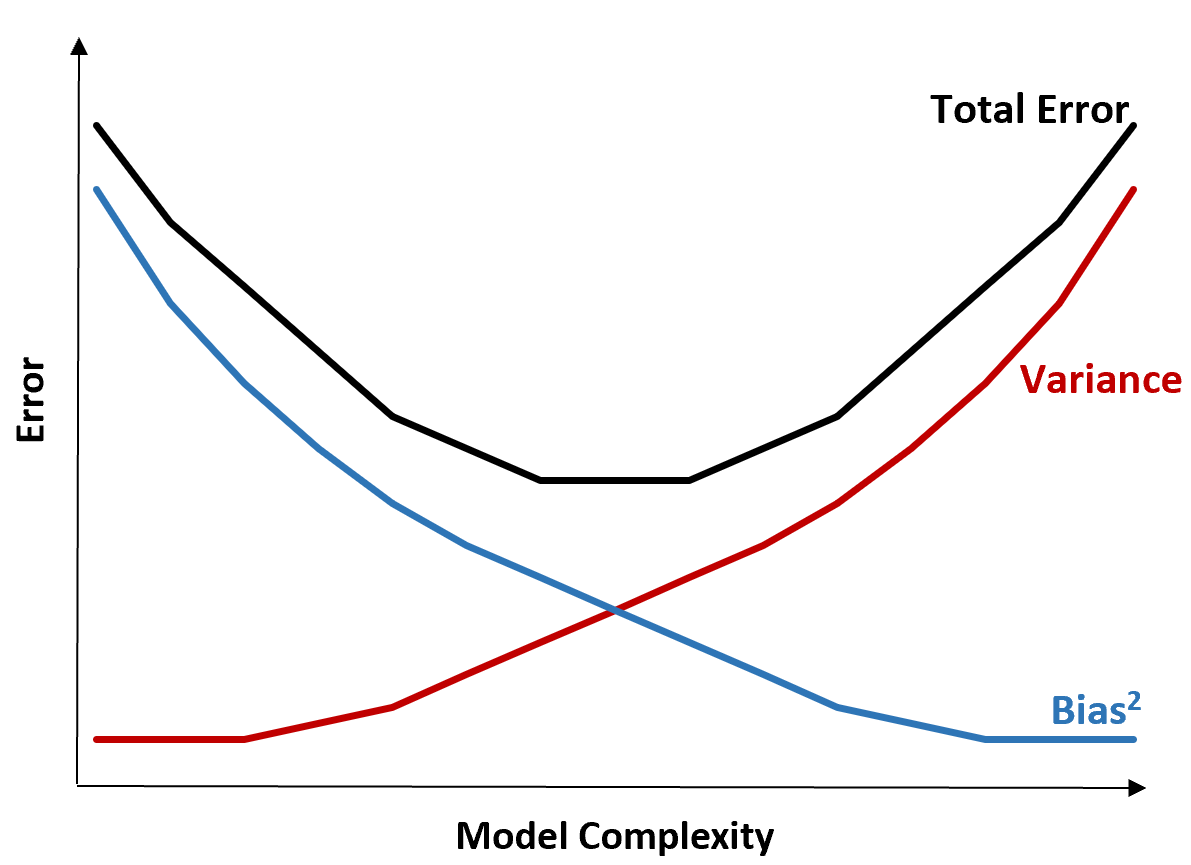
Modelin karmaşıklığı arttıkça toplam hata azalır, ancak bu yalnızca belirli bir noktaya kadar olur. Belirli bir noktadan sonra varyans artmaya başlar ve toplam hata da artmaya başlar.

Uygulamada, yalnızca bir modelin toplam hatasını en aza indirmeyi önemsiyoruz, varyansı veya önyargıyı mutlaka en aza indirmeyi değil. Toplam hatayı en aza indirmenin yolunun varyans ve önyargı arasında doğru dengeyi bulmak olduğu ortaya çıktı.

Başka bir deyişle, açıklayıcı değişkenler ile yanıt değişkeni arasındaki gerçek ilişkiyi yakalayacak kadar karmaşık, ancak gerçekte var olmayan kalıpları tespit edemeyecek kadar karmaşık olmayan bir model istiyoruz.

Bir model çok karmaşık olduğunda verilere gereğinden fazla uyum sağlar . Bunun nedeni, eğitim verilerinde şans eseri oluşan kalıpları bulmanın çok zor olmasıdır. Bu tür bir modelin görünmez veriler üzerinde düşük performans göstermesi muhtemeldir.

Ancak bir model çok basit olduğunda verileri küçümser . Bunun nedeni, açıklayıcı değişkenler ile yanıt değişkeni arasındaki gerçek ilişkinin gerçekte olduğundan daha basit olduğunun varsayılmasıdır.

Makine öğreniminde en uygun modelleri seçmenin yolu, modeli gelecekteki görünmeyen veriler üzerinde test etme hatasını en aza indirmek için önyargı ve varyans arasında bir denge bulmaktır.

Uygulamada testlerin MSE’sini en aza indirmenin en yaygın yolu çapraz doğrulama kullanmaktır.