Histogram

Bu makalede histogramın ne olduğu, ne için kullanıldığı ve histogramın nasıl yorumlanacağı açıklanmaktadır. Böylece histogramın nasıl yapıldığını ve her tür histogramın örneklerini keşfedeceksiniz.

Histogram nedir?

Histogram , bir dizi istatistiksel verinin dikdörtgen çubuklarla temsil edildiği, böylece histogramdaki her çubuğun karşılık gelen frekansıyla orantılı olduğu bir istatistiksel grafik türüdür.

Histogramlar, istatistiksel bir örneğin ağırlığı gibi sürekli değişkenlerin grafiğini çizmek için kullanılır. Ek olarak histogram, bir dağılımın şeklini hızlı bir şekilde görselleştirmenize olanak tanır.

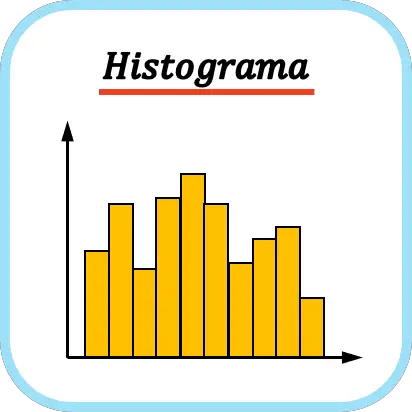
Frekans histogramındaki her çubuk, aralığın genişliğiyle orantılı bir genişliğe ve aralığın frekansıyla orantılı bir yüksekliğe sahiptir.

Histogram nasıl yapılır

Histogram oluşturma adımları şunlardır:

1. Histogramın yatay eksenini veri serisine göre gruplara bölün.
2. Aralık frekans değerlerini histogramın dikey eksenine çizin.
3. Her aralık için yüksekliği aralığın frekansına eşit olan dikdörtgen bir çubuk çizin. Ardışık iki aralığın çubuklarının birbirine değmesi gerektiğini unutmayın.

histogram örneği

Histogramın tanımını ve ilgili teoriyi gördükten sonra, aşağıda bu tür bir istatistiksel grafiğin nasıl oluşturulduğunun açıklanmış bir örneğini görebilirsiniz.

• Bir giyim mağazası aşağıdaki sıklık tablosunda görüldüğü gibi gün içerisinde 50 adet farklı fiyattan satış yapmaktadır. Kaydedilen satış verilerinden bir histogram oluşturun.

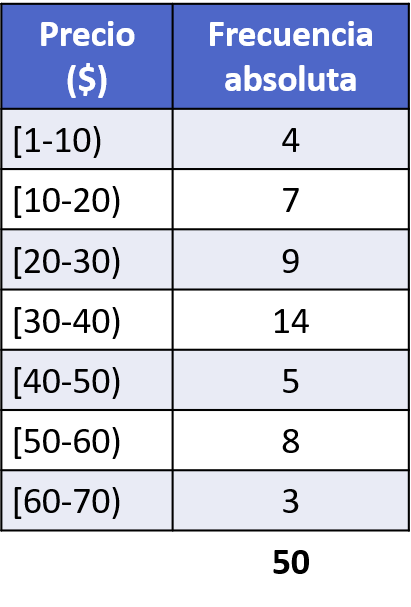
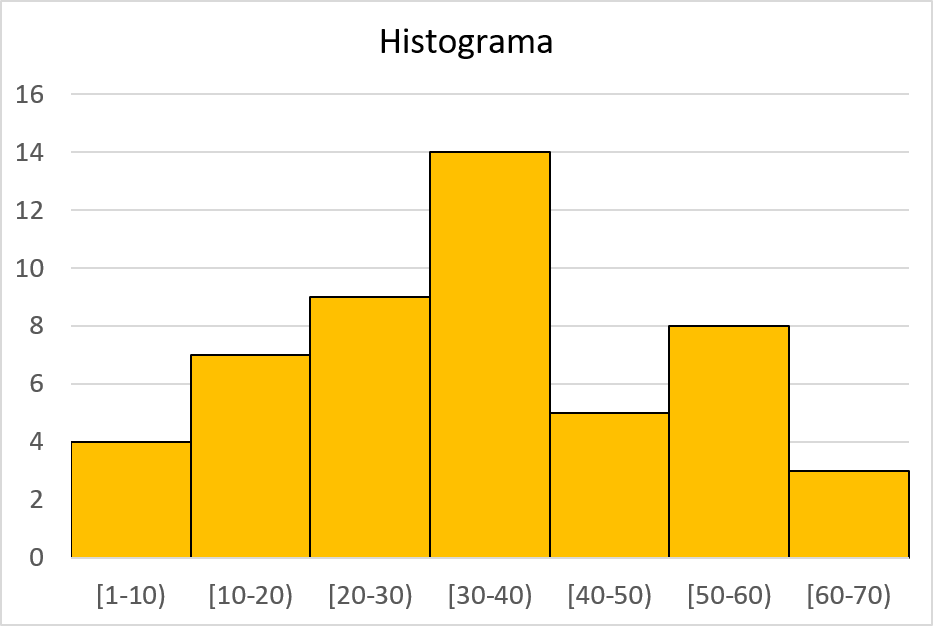
Bir histogramı temsil etmek için yukarıda açıklanan adımları izlememiz gerekir. Yani, önce yatay ekseni verinin aralıklarına eşdeğer parçalara bölüyoruz, sonra dikey eksenin ölçeğini ölçeklendiriyoruz ve son olarak her aralığı, mutlak frekansında eşit yükseklikte bir sütunla temsil ediyoruz.

Göreceli frekans histogramı

Göreli frekans histogramı, veri kümesinin göreceli frekanslarının temsil edildiği bir histogram türüdür. Yani mutlak frekansların grafiğini çizmek yerine bağıl frekansların grafiğini çiziyoruz.

Her ne kadar farklı frekanslar temsil edilse de, göreceli frekans histogramının şekli mutlak frekans histogramının şekliyle aynıdır, sadece dikey eksendeki değerleri değiştirirler.

Örnek olarak, önceki alıştırmanın istatistiksel çalışmasından bağıl frekans histogramını oluşturacağız. Bunu yapmak için öncelikle her aralığın mutlak frekansının toplam veri sayısına (50) bölünmesine eşdeğer olan bağıl frekansını hesaplamamız gerekir.

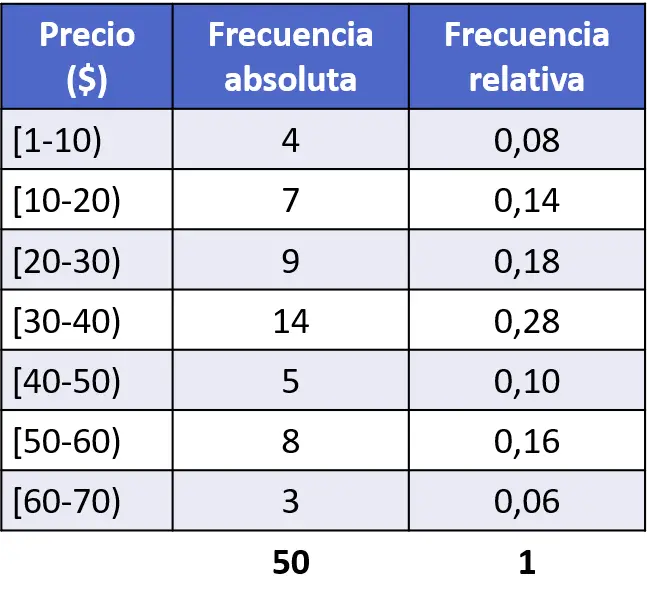
Göreceli frekansları hesapladıktan sonra bunları bir histogramda grafik haline getiririz. Bunu yapmak için, satılan birimlerin fiyatlarına karşılık gelen yatay ekseni, ardından göreceli frekansların temsil edildiği dikey ekseni ve son olarak her aralık için, göreceli frekansına eşdeğer yükseklikte dikdörtgen bir çubuk çizeriz. . sıklık.

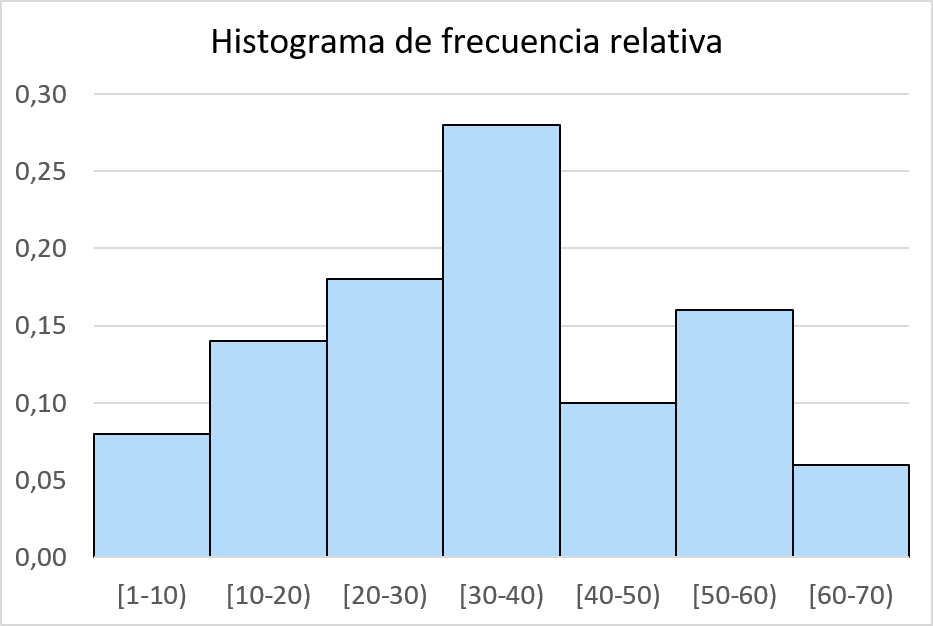
Kümülatif frekans histogramı

Az önce mutlak frekans histogramının ve bağıl frekans histogramının nasıl oluşturulacağını gördük, ancak kümülatif frekans histogramları istatistikte de kullanılır.

Kümülatif frekans histogramı, kümülatif frekansların çizildiği bir histogram türüdür. Yani, kümülatif frekans histogramında mutlak frekanslar yerine kümülatif frekanslar temsil edilir.

Mantıksal olarak mutlak ve bağıl frekanslarla kümülatif bir frekans histogramı yapılabilir. Örnek olarak, bu iki tür histogram, bu makale boyunca yaptığımız alıştırmayla aynı veriler kullanılarak aşağıda temsil edilecektir.

Kümülatif mutlak frekansların histogramı

Açıkçası, kümülatif mutlak frekansların histogramını çizmek için öncelikle her aralık için kümülatif mutlak frekansları belirlememiz gerekir. Bunu yapmak için, her aralıktaki önceki tüm mutlak frekansları artı söz konusu aralığın mutlak frekansını toplarız:

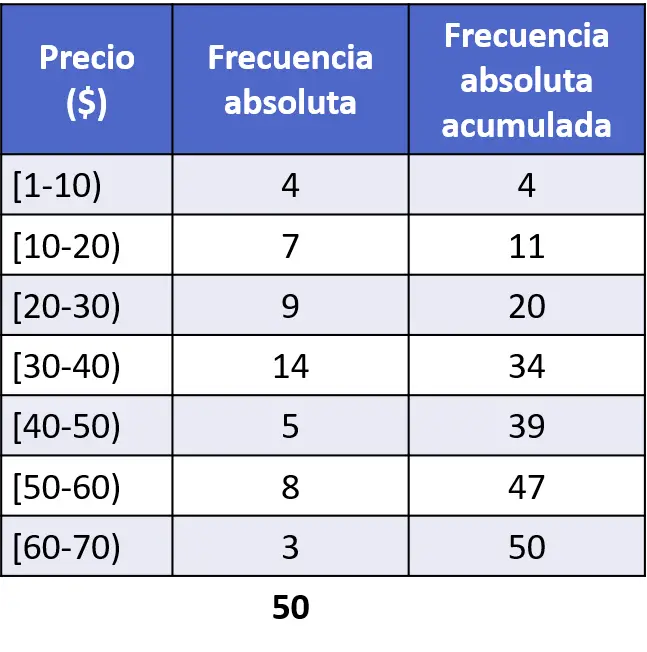
Artık matematiği yaptığımıza göre, histogramı çizmek için aynı prosedürü kümülatif mutlak frekanslarla takip ediyoruz:

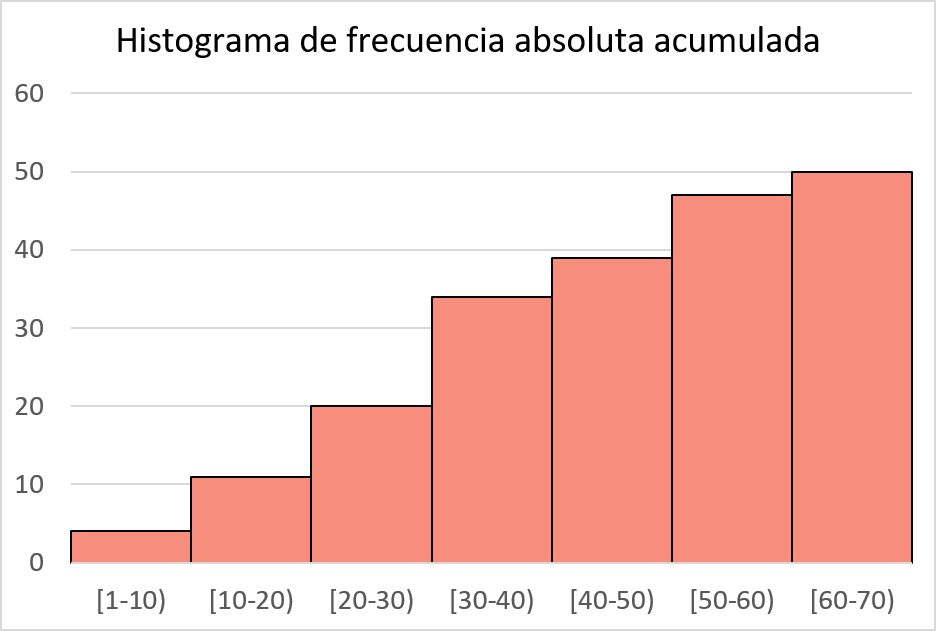
Kümülatif bağıl frekansların histogramı

Kümülatif göreli frekansların histogramı, kümülatif mutlak frekanslarla aynı şekilde üretilir; önce veri serisinin kümülatif göreli frekanslarını hesaplarız:

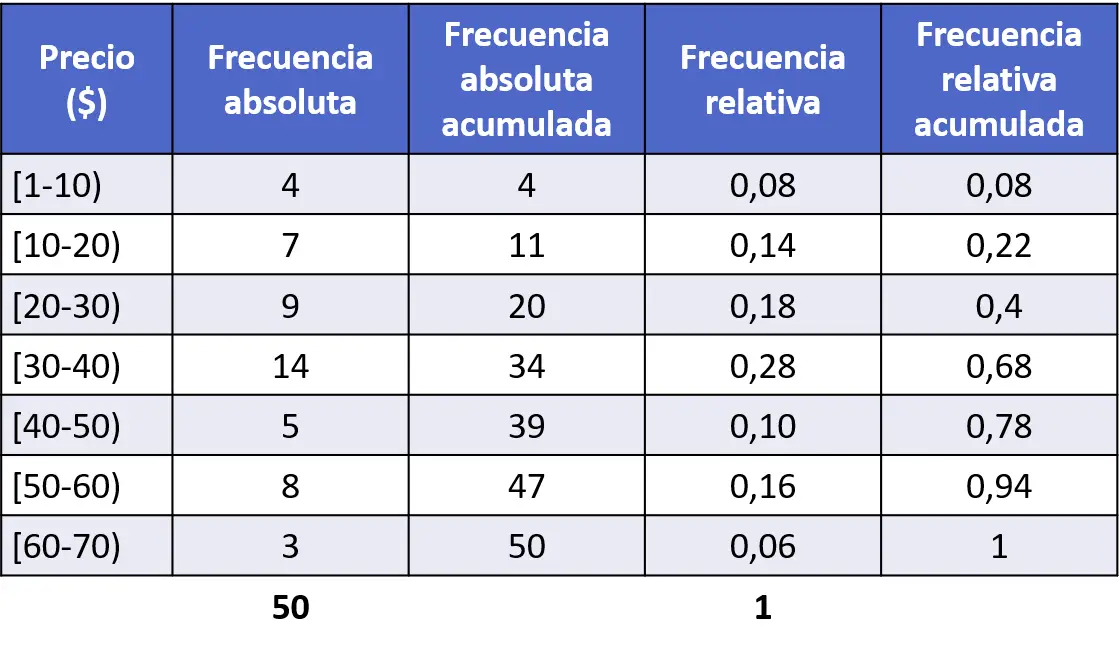
Daha sonra kümülatif bağıl frekansı bir histogramda temsil ediyoruz:

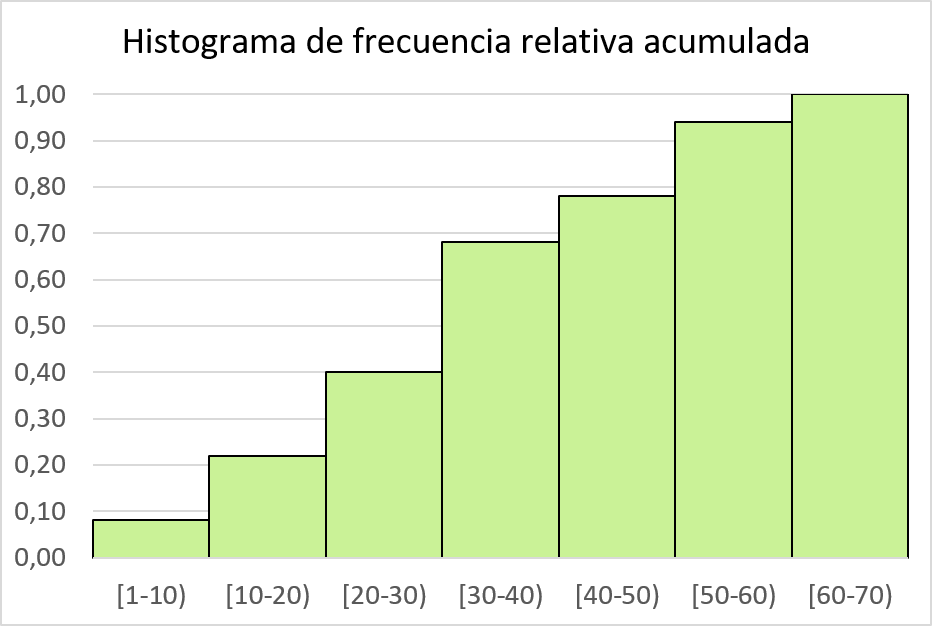
Histogramı frekans poligonuyla birleştirin

Bazen istatistiklerde histogram, düz çizgilerle birbirine bağlanan bir dizi nokta olan bir frekans poligonuyla birleştirilir. Bu şekilde, frekans poligonunun çizgisi veri serisinin ilerleyişini daha iyi görselleştirmenize olanak tanıdığından, verilerin gelişimi daha net bir şekilde gösterilir.

Bu iki tür istatistiksel grafiği birleştirmek için, her dikdörtgen histogram çubuğunun üst kısmının ortasına bir nokta çizin ve ardından ardışık noktaları düz çizgilerle birleştirin.

Örneğin, bu yazının başında üretilen mutlak frekansların bir frekans poligonuyla birleştirilmiş histogramı şöyledir: