Sınıflandırma ve regresyon ağaçlarına giriş

Bir dizi yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişki doğrusal olduğunda, çoklu doğrusal regresyon gibi yöntemler, doğru öngörücü modeller üretebilir.

Bununla birlikte, bir dizi öngörü ile bir yanıt arasındaki ilişki oldukça doğrusal olmayan ve karmaşık olduğunda, doğrusal olmayan yöntemler daha iyi performans gösterebilir.

Doğrusal olmayan bir yöntemin bir örneği, genellikle CART olarak kısaltılan sınıflandırma ve regresyon ağaçlarıdır .

Adından da anlaşılacağı gibi, CART modelleri bir yanıt değişkeninin değerini tahmin eden karar ağaçları oluşturmak için bir dizi öngörücü değişken kullanır.

Örneğin, yüzlerce profesyonel beyzbol oyuncusu için Oynanan Yıl ve Ortalama Ev Koşusu tahmin değişkenlerini ve yıllık Maaş yanıt değişkenini içeren bir veri setimiz olduğunu varsayalım.

Bu veri kümesi için bir regresyon ağacı şöyle görünebilir:

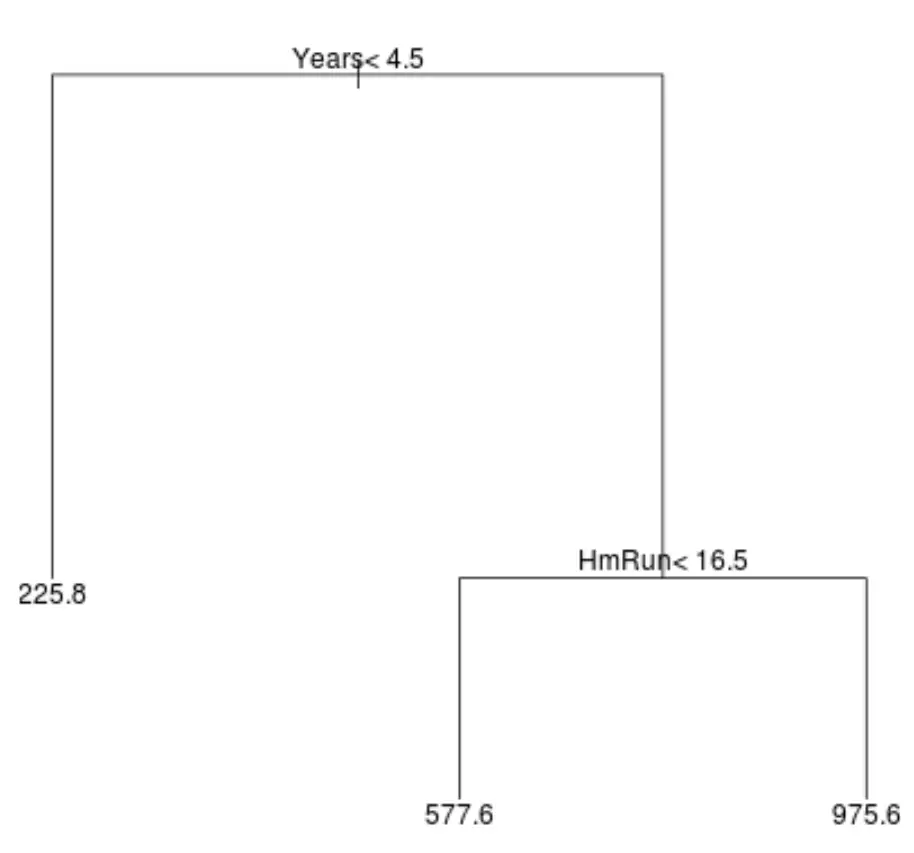
Ağacı yorumlamanın yolu aşağıdaki gibidir:

• 4,5 yıldan az oynayan oyuncuların tahmini maaşı 225,8 bin dolar.
• 4,5 yıldan fazla veya daha fazla oynayan ve ortalama 16,5’ten az home run yapan oyuncuların tahmini maaşı 577,6 bin dolar olacak.
• 4,5 yıl veya daha fazla oyun deneyimi olan ve ortalama 16,5 veya daha fazla home run yapan oyuncuların beklenen maaşı 975,6 bin dolar.

Bu modelin sonuçları sezgisel olarak anlamlı olmalıdır: Daha uzun yıllara dayanan deneyime sahip ve daha fazla sayıda ortalama home run yapan oyuncular daha yüksek maaş kazanma eğilimindedir.

Daha sonra bu modeli yeni bir oyuncunun maaşını tahmin etmek için kullanabiliriz.

Örneğin, belirli bir oyuncunun 8 yıl oynadığını ve yılda ortalama 10 home run yaptığını varsayalım. Modelimize göre bu oyuncunun yıllık maaşının 577,6 bin dolar olacağını tahmin ediyoruz.

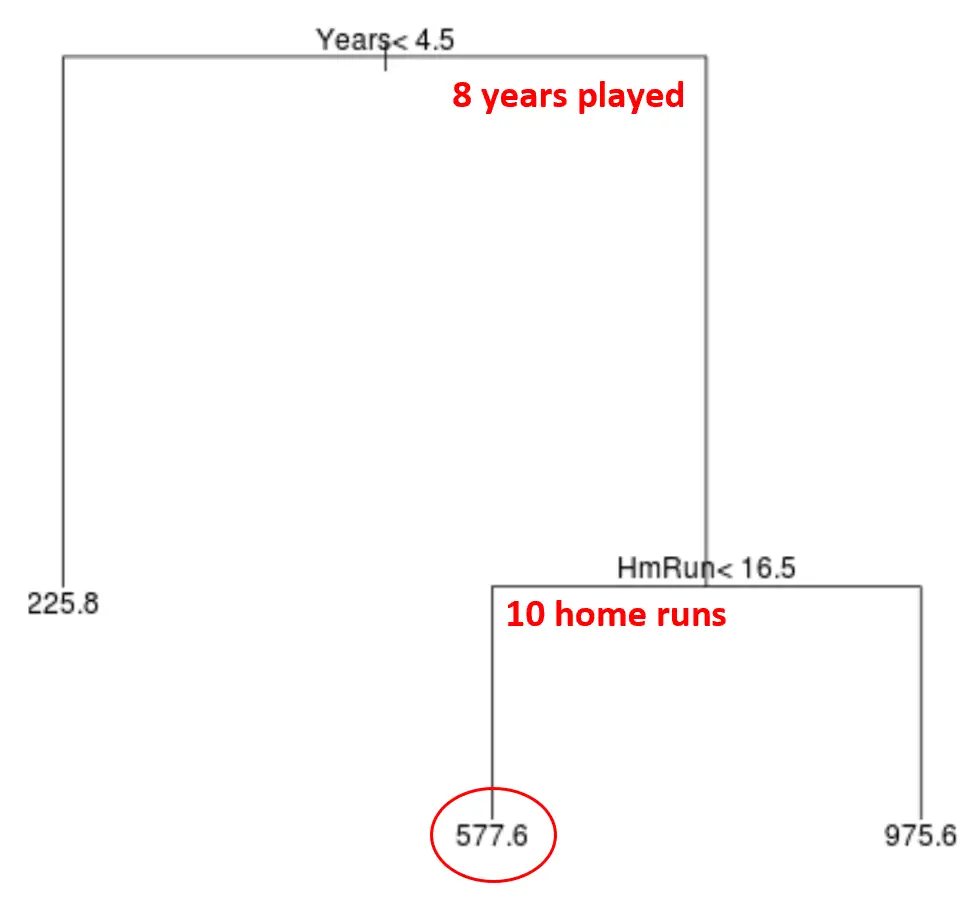
Ağaçla ilgili bazı açıklamalar:

• Ağacın tepesinde yer alan ilk yordayıcı değişken en önemlisidir, yani yanıt değişkeninin değerinin tahminini en çok etkileyen değişkendir. Bu durumda, oynanan yıllar maaşı devre ortalamasından daha iyi tahmin ediyor.
• Ağacın alt kısmındaki bölgelere yaprak düğümleri denir. Bu özel ağacın üç terminal düğümü vardır.

CART modelleri oluşturma adımları

Belirli bir veri kümesi için CART modeli oluşturmak için aşağıdaki adımları kullanabiliriz:

Adım 1: Eğitim verileri üzerinde büyük bir ağaç büyütmek için özyinelemeli ikili bölmeyi kullanın.

İlk olarak, aşağıdaki yöntemi kullanarak bir regresyon ağacını büyütmek için özyinelemeli ikili bölme adı verilen açgözlü bir algoritma kullanıyoruz:

• Tüm yordayıcı değişkenleri (X _{1 ,} X ₂ , … , artık standart hata) en düşük olarak düşünün. .
  • Sınıflandırma ağaçları için, tahmin ediciyi ve kesme noktasını, sonuçta ortaya çıkan ağacın en düşük sınıflandırma hata oranına sahip olmasını sağlayacak şekilde seçiyoruz.
• Yalnızca her terminal düğümünün belirli bir minimum gözlem sayısından daha azına sahip olduğu zaman durarak bu işlemi tekrarlayın.

Bu algoritma açgözlüdür çünkü ağaç oluşturma sürecinin her adımında, geleceğe bakmak ve gelecek aşamada daha iyi bir ağaç geneline yol açacak bir bölünme seçmek yerine, yalnızca o adıma dayalı olarak yapılacak en iyi bölünmeyi belirler.

Adım 2: α’ya dayalı olarak en iyi ağaçların sırasını elde etmek için büyük ağaca maliyet karmaşıklığı budaması uygulayın.

Büyük ağacı büyüttükten sonra, karmaşık budama olarak bilinen ve aşağıdaki gibi çalışan bir yöntemi kullanarak onu budamamız gerekir:

• T terminal düğümlerine sahip olası her ağaç için RSS + α|T|’yi en aza indiren ağacı bulun.
• α değerini arttırdığımızda daha fazla terminal düğümü olan ağaçların cezalandırılacağını unutmayın. Bu, ağacın çok karmaşık hale gelmemesini sağlar.

Bu süreç, her bir α değeri için en iyi ağaçların sıralanmasıyla sonuçlanır.

Adım 3: α’yı seçmek için k-katlı çapraz doğrulamayı kullanın .

Her bir α değeri için en iyi ağacı bulduğumuzda, test hatasını en aza indiren α değerini seçmek için k-katlı çapraz doğrulama uygulayabiliriz.

Adım 4: Son şablonu seçin.

Son olarak, seçilen α değerine karşılık gelen son modeli seçiyoruz.

CART modellerinin avantajları ve dezavantajları

CART modelleri aşağıdaki avantajları sunar:

• Yorumlanması kolaydır.
• Açıklamaları kolaydır.
• Görselleştirmeleri kolaydır.
• Hem regresyon hem de sınıflandırma problemlerine uygulanabilirler.

Ancak CART modellerinin aşağıdaki dezavantajları vardır:

• Diğer doğrusal olmayan makine öğrenimi algoritmaları kadar tahmin doğruluğuna sahip olma eğilimindedirler. Ancak birçok karar ağacının torbalama, güçlendirme ve rastgele ormanlar gibi yöntemlerle kümelenmesiyle tahmin doğrulukları artırılabilir.

İlgili: R’ye sınıflandırma ve regresyon ağaçları nasıl sığdırılır