R'de örnekleme dağılımları nasıl hesaplanır?

Örnekleme dağılımı, belirli bir istatistiğin tek bir popülasyondan birçok rastgele örneğe dayanan olasılık dağılımıdır.

Bu eğitimde R’deki örnekleme dağılımlarıyla aşağıdakilerin nasıl yapılacağı açıklanmaktadır:

• Bir örnekleme dağılımı oluşturun.
• Örnekleme dağılımını görselleştirin.
• Örnekleme dağılımının ortalamasını ve standart sapmasını hesaplayın.
• Örnekleme dağılımına ilişkin olasılıkları hesaplayın.

R’de bir örnekleme dağılımı oluşturun

Aşağıdaki kod, R’de bir örnekleme dağılımının nasıl oluşturulacağını gösterir:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

Bu örnekte, her örnek boyutunun 20 olduğu ve ortalaması 5,3 ve standart sapması 9 olan normal bir dağılımdan oluşturulan 10.000 örneğin ortalamasını hesaplamak için rnorm() işlevini kullandık.

İlk numunenin ortalamasının 5,283992 olduğunu, ikinci numunenin ortalamasının 6,304845 olduğunu vb. görebiliriz.

Örnekleme dağılımını görselleştirin

Aşağıdaki kod, örnekleme dağılımını görselleştirmek için basit bir histogramın nasıl oluşturulacağını gösterir:

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

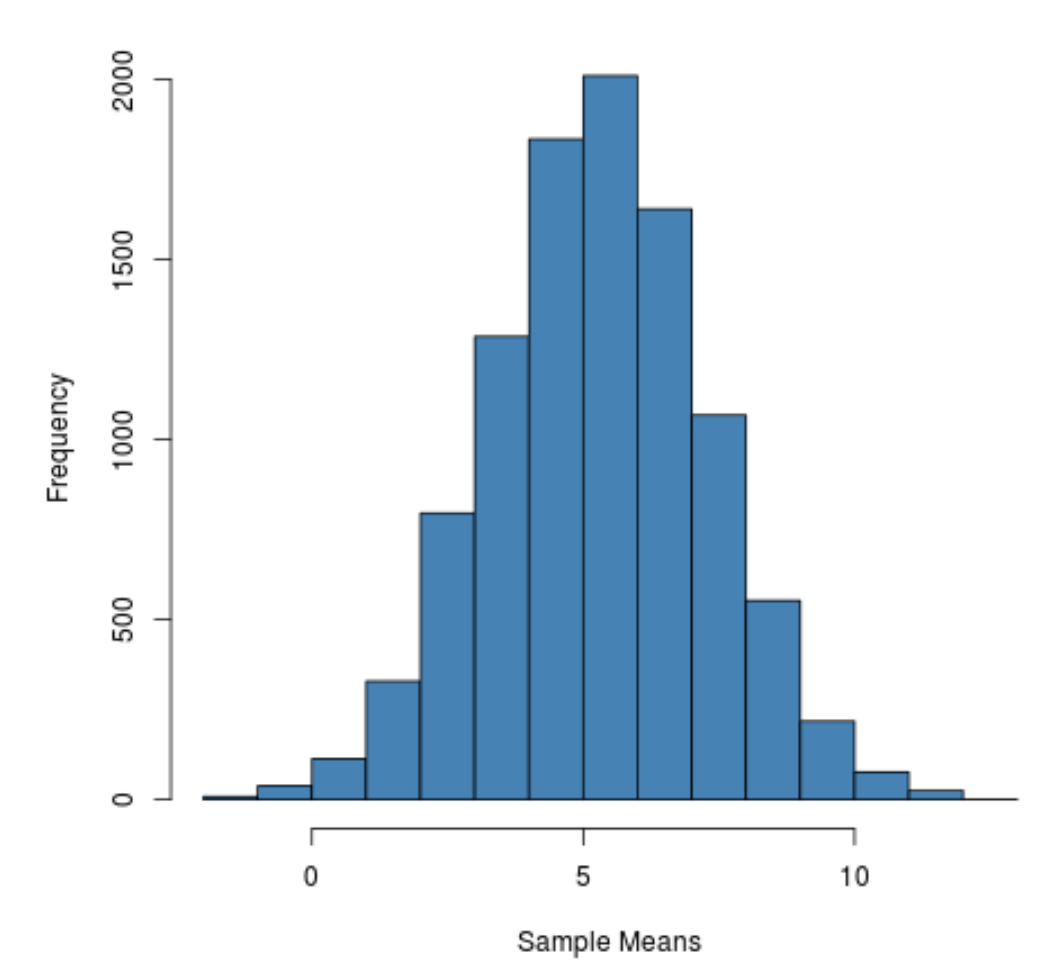
Örnekleme dağılımının çan şeklinde olduğu ve 5 değerine yakın bir zirveye sahip olduğu görülebilir.

Ancak dağılımın kuyruklarından bazı örneklerin ortalamalarının 10’dan büyük, bazılarının ise 0’dan küçük ortalamalara sahip olduğunu görebiliriz.

Ortalamayı ve standart sapmayı bulun

Aşağıdaki kod örnekleme dağılımının ortalama ve standart sapmasının nasıl hesaplanacağını gösterir:

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

Teorik olarak örnekleme dağılımının ortalaması 5,3 olmalıdır. Bu örnekte gerçek örnek ortalamanın 5,3’e yakın olan 5,287195 olduğunu görebiliriz.

Ve teorik olarak örnekleme dağılımının standart sapması s/√n’ye eşit olmalıdır, bu da 9 / √20 = 2,012 olacaktır. Örnekleme dağılımının gerçek standart sapmasının 2,012’ye yakın olan 2,00224 olduğunu görebiliriz.

Olasılıkları hesaplayın

Aşağıdaki kod, popülasyon ortalaması, popülasyon standart sapması ve örnek boyutu göz önüne alındığında, örnek ortalaması için belirli bir değer elde etme olasılığının nasıl hesaplanacağını gösterir.

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Bu özel örnekte, popülasyon ortalamasının 5,3, popülasyon standart sapmasının 9 ve 20’lik numune boyutunun 0,6417 olduğu göz önüne alındığında, numune ortalamasının 6’dan küçük veya 6’ya eşit olma olasılığını buluyoruz.

Bu, Örnekleme Dağıtımı Hesaplayıcısı tarafından hesaplanan olasılığa çok yakındır:

Kodun tamamı

Bu örnekte kullanılan R kodunun tamamı aşağıda gösterilmiştir:

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

Ek kaynaklar

Örnekleme Dağılımlarına Giriş
Örnekleme Dağıtımı Hesaplayıcı
Merkezi Limit Teoremine Giriş