Mutlak ortalama sapma ve standart sapma: fark nedir?
Standart sapma, bir veri kümesinin yayılmasını ölçmenin en yaygın yollarından biridir.
Aşağıdaki şekilde hesaplanır:
Standart sapma = √( Σ(x ben – x ) 2 / n )
Bir veri setindeki gözlemlerin dağılımını ölçmenin bir başka yolu da ortalama mutlak sapmadır .
Aşağıdaki şekilde hesaplanır:
Ortalama mutlak sapma = Σ|x i – x | /Olumsuz
Bu eğitimde, bu iki ölçüm arasındaki farklar, her birinin nasıl hesaplanacağına ilişkin örneklerle birlikte açıklanmaktadır.
Benzerlikler ve farklılıklar
Adından da anlaşılacağı gibi, standart sapma ve ortalama mutlak sapma, belirli bir veri kümesindeki gözlemlerin ortalamadan tipik sapmasını ölçmeye çalışır.
Ancak her metriğin kullandığı yöntem farklıdır.
Standart sapma
Standart sapma, her bir gözlem ile bir veri kümesinin ortalaması arasındaki kare farkını bulur. Daha sonra bu kare farkların ortalamasını alır ve karekökünü alır.
Bu bize bir gözlemin ortalamadan “standart”ını veya tipik sapmasını temsil eden bir sayı bırakır.
Mutlak sapma anlamına gelir
Tersine, ortalama mutlak sapma, her gözlem ile veri kümesinin ortalaması arasındaki mutlak sapmayı bulur. Daha sonra bu sapmaların ortalamasını bulur.
Bu bize gözlemlerin ortalamadan ortalama sapmasını temsil eden bir sayıyla kalıyor.
Standart sapma, farkların karesini bulduğu için her zaman ortalama mutlak sapmaya eşit veya ondan büyük olacaktır.
Aşırı aykırı değerler mevcut olduğunda standart sapma, ortalama mutlak sapmadan önemli ölçüde daha büyük olacaktır. Aşağıdaki örnek bu noktayı göstermektedir.
Örnek: standart sapmadan ortalama mutlak sapma
Aşağıdaki 8 değerden oluşan veri setine sahip olduğumuzu varsayalım:
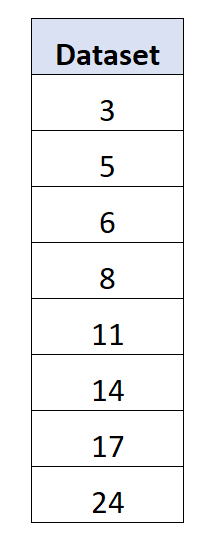
Ortalama 11 çıkıyor.
Yani ortalama mutlak sapmayı şu şekilde hesaplayabiliriz:
Ortalama mutlak sapma = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5,5 .
Ve standart sapmayı şu şekilde hesaplayacağız:
Standart sapma = √((3-11) 2 + (5-11) 2 + (6-11) 2 + (8-11) 2 + (11-11) 2 + (14-11) 2 + (17- 11) 2 + (24-11) 2 )/8) = 6,595 .
Daha önce de belirtildiği gibi standart sapma her zaman ortalama mutlak sapmaya eşit veya ondan büyük olacaktır.
Ancak veri setinde aşırı aykırı değerler varsa, standart sapma ile ortalama mutlak sapma arasındaki fark özellikle büyük olacaktır.
Örneğin, son değer için aşırı uç değere sahip aşağıdaki veri kümesini göz önünde bulundurun:
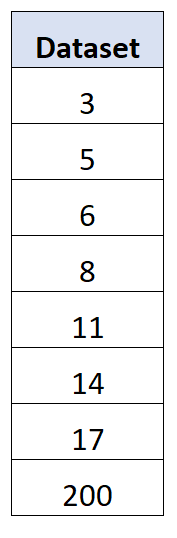
Bu veri seti için standart sapmanın 63,27 , ortalama mutlak sapmanın ise 41,75 olduğu ortaya çıktı.
Aşırı aykırı değer, standart sapmanın ortalama mutlak sapmadan çok daha büyük olmasına neden olur.
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil