R'de niceliksel regresyon nasıl gerçekleştirilir

Doğrusal regresyon, bir veya daha fazla yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir yöntemdir.

Tipik olarak doğrusal regresyon uyguladığımızda yanıt değişkeninin ortalama değerini tahmin etmek isteriz.

Bununla birlikte, yanıt değerinin herhangi bir nicelik veya yüzdelik değerini (70. yüzdelik dilim, 90. yüzdelik dilim, 98. yüzdelik dilim vb.) tahmin etmek için bunun yerine nicelik regresyonu olarak bilinen bir yöntemi kullanabiliriz.

R’de niceliksel regresyon gerçekleştirmek için, aşağıdaki sözdizimini kullanan quantreg paketindeki rq() işlevini kullanabiliriz:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

Altın:

• y: yanıt değişkeni
• x: tahmin değişken(ler)i
• veri: veri kümesinin adı
• tau: Bulunacak yüzdelik dilim. Varsayılan değer medyandır (tau = 0,5), ancak bunu 0 ile 1 arasında herhangi bir sayıya ayarlayabilirsiniz.

Bu eğitimde, R’de niceliksel regresyon gerçekleştirmek için bu işlevin nasıl kullanılacağına ilişkin adım adım bir örnek sunulmaktadır.

1. Adım: Verileri girin

Bu örnek için bir üniversitede 100 farklı öğrencinin ders çalışma saatlerini ve elde ettiği sınav sonuçlarını içeren bir veri seti oluşturacağız:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

Adım 2: Kantil Regresyon Gerçekleştirin

Daha sonra, yordayıcı değişken olarak çalışılan saatleri ve yanıt değişkeni olarak sınav puanlarını kullanarak niceliksel bir regresyon modeli uygulayacağız.

Bu modeli, çalışılan saat sayısına bağlı olarak sınav puanlarının beklenen yüzde 90’lık dilimini tahmin etmek için kullanacağız:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

Sonuçtan tahmini regresyon denklemini görebiliriz:

90. yüzdelik sınav puanı = 60,25 + 2,437*(saat)

Örneğin 8 saat eğitim gören tüm öğrencilerin 90. yüzdelik puanı 79,75 olmalıdır:

Sınav puanının 90. yüzdelik dilimi = 60,25 + 2,437*(8) = 79,75 .

Çıktı ayrıca tahmin değişkeninin kesişme noktası ve süreleri için üst ve alt güven sınırlarını da görüntüler.

3. Adım: Sonuçları görselleştirin

Grafiğe yerleştirilmiş niceliksel regresyon denklemi ile bir dağılım grafiği oluşturarak regresyon sonuçlarını da görselleştirebiliriz:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

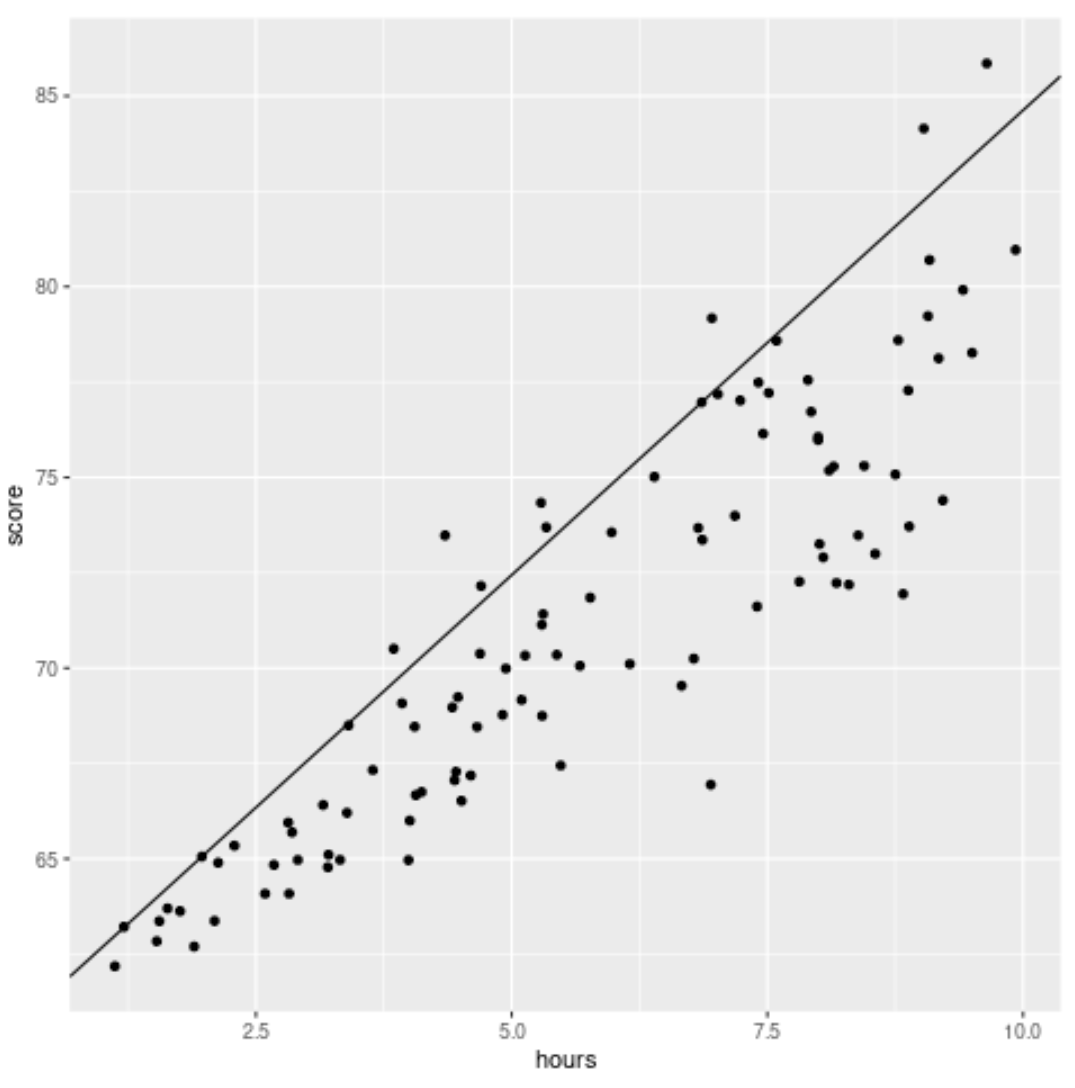
Geleneksel doğrusal regresyon çizgisinin aksine, bu uydurulmuş çizginin verilerin merkezinden geçmediğini unutmayın. Bunun yerine, yordayıcı değişkenin her düzeyinde tahmini 90. yüzdelik dilimden geçer.

Uydurulmuş kantil regresyon denklemi ile basit doğrusal regresyon denklemi arasındaki farkı geom_smooth() argümanını ekleyerek görebiliriz:

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

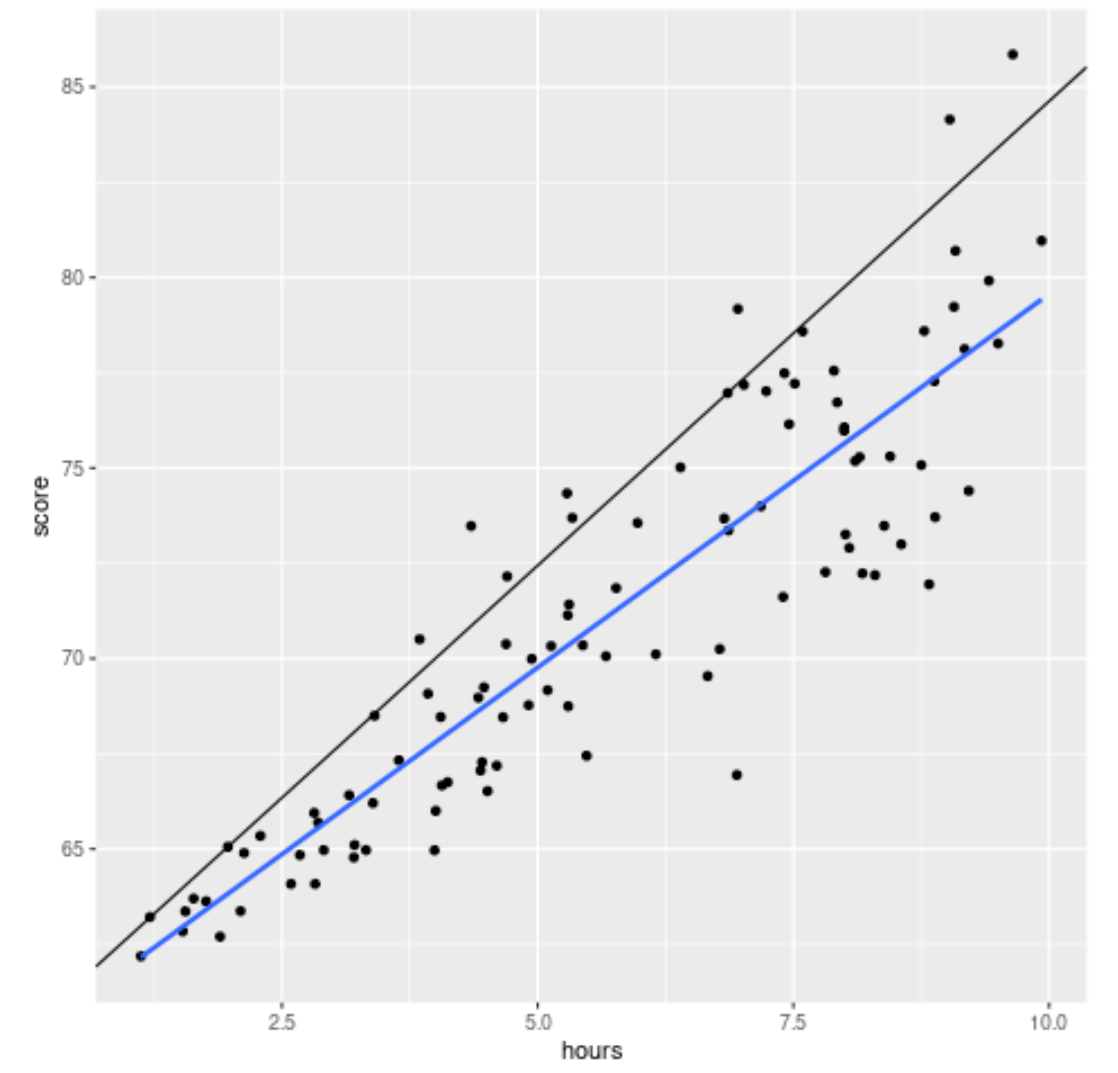
Siyah çizgi, 90’ıncı yüzdelik için ayarlanan kantil regresyon çizgisini, mavi çizgi ise yanıt değişkeninin ortalama değerini tahmin eden basit doğrusal regresyon çizgisini gösterir.

Beklendiği gibi, basit doğrusal regresyon çizgisi veriler üzerinden geçiyor ve bize her saat düzeyinde sınav puanlarının tahmini ortalama değerini gösteriyor.

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de ikinci dereceden regresyon nasıl gerçekleştirilir?