Kutu grafikleri nasıl karşılaştırılır: örneklerle

Kutu grafiği, aşağıdakileri içeren bir veri kümesinin beş basamaklı özetini görüntüleyen bir grafik türüdür:

• Asgari değer
• İlk çeyrek (25. yüzdelik dilim)
• Medyan değer
• Üçüncü çeyrek (75. yüzdelik dilim)
• Maksimum değer

Bir kutu grafiği oluşturmak için birinci çeyrekten üçüncü çeyreğe kadar bir kutu çizeriz. Daha sonra ortancaya dikey bir çizgi çiziyoruz. Son olarak çeyreklerin “bıyıklarını” minimum ve maksimum değere kadar çiziyoruz.

Kutu grafikleri kullanışlıdır çünkü bir veri kümesindeki değerlerin dağılımını hızlı bir şekilde anlamamıza olanak tanır. Ayrıca iki farklı veri kümesini karşılaştırmak için de kullanışlıdırlar.

İki veya daha fazla kutu grafiğini karşılaştırırken dört farklı soruyu yanıtlayabiliriz:

1. Medyan değerler nasıl karşılaştırılır? Hangi veri setinin daha yüksek medyan değerine sahip olduğunu belirlemek için her kutudaki dikey çizgiyi karşılaştırabiliriz.

2. Dağılım nasıl karşılaştırılır? Hangi veri setinin daha büyük olduğunu belirlemek için her kutunun uzunluğunu (Q1 ve Q3 arasındaki mesafeyi (çeyrekler arası aralık) temsil eden) karşılaştırabiliriz.

3. Asimetri nasıl karşılaştırılır? Dikey çizgi ilk çeyreğe ne kadar yakınsa veri seti o kadar pozitif çarpıktır. Dikey çizgi üçüncü çeyreğe ne kadar yakınsa veri seti o kadar çarpıktır.

4. Aykırı değerler mevcut mu? Kutu grafiklerinde aykırı değerler genellikle her bir çizginin ötesine uzanan küçük dairelerle temsil edilir. Bir gözlem, aşağıdaki kriterlerden birini karşılıyorsa aykırı değer olarak tanımlanır:

• Bir gözlem Q1 – 1,5*IQR’den az
• Bir gözlemin Q3 + 1,5*IQR’den büyük olması

Aşağıdaki örnek, iki farklı kutu grafiğinin nasıl karşılaştırılacağını ve bu dört sorunun nasıl yanıtlanacağını gösterir.

Örnek: Kutu Grafiklerini Karşılaştırma

Aşağıdaki veri kümeleri sınava hazırlanmak için iki çalışma tekniğinden birini kullanan öğrencilerin sonuçlarını göstermektedir:

Yöntem 1: 78, 78, 79, 80, 80, 82, 82, 83, 83, 86, 86, 86, 86, 87, 87, 87, 88, 88, 88, 91

Yöntem 2: 66, 66, 66, 67, 68, 70, 72, 75, 75, 78, 82, 83, 86, 88, 89, 90, 93, 94, 95, 98

Her veri kümesi için kutu grafikleri oluşturursak şöyle görünürler:

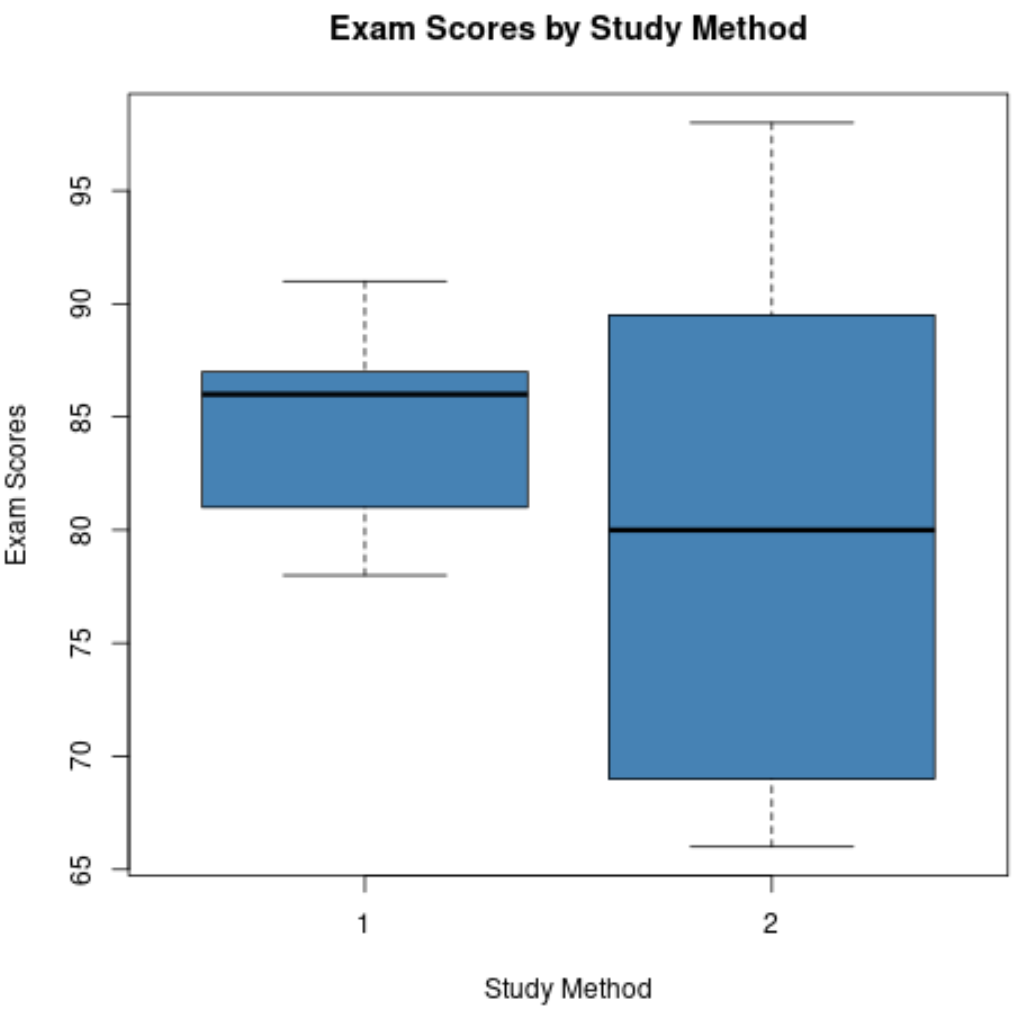
Bu iki kutu grafiğini karşılaştırabilir ve aşağıdaki dört soruyu yanıtlayabiliriz:

1. Medyan değerler nasıl karşılaştırılır? Çalışma yöntemi 1 için kutu grafiğinin ortasındaki çizgi, çalışma yöntemi 2’nin çizgisinden daha yüksektir; bu, çalışma yöntemi 1’i kullanan öğrencilerin daha yüksek sınavda ortalama nota sahip olduğunu gösterir.

2. Dağılım nasıl karşılaştırılır? Çalışma Yöntemi 2’nin kutu grafiği, Çalışma Yöntemi 1’in kutu grafiğinden çok daha uzundur; bu da sınav puanlarının Çalışma Yöntemi 2’yi kullanan öğrenciler arasında çok daha fazla dağıtıldığını gösterir.

3. Asimetri nasıl karşılaştırılır? Çalışma yöntemi 1 için kutu grafiğinin ortasındaki çizgi Q3’e yakındır; bu, çalışma yöntemi 1’i kullanan öğrencilerin sınav puanlarının dağılımının olumsuz yönde çarpık olduğunu gösterir. Tersine, çalışma yöntemi 2 için kutu grafiğinin ortasındaki çizgi kutunun merkezine yakındır, bu da puanların dağılımının minimum düzeyde çarpık olduğu anlamına gelir.

4. Aykırı değerler mevcut mu? Her iki kutu grafiği de üst veya alt çizgilerin ötesine uzanan küçük dairelere sahip değil; bu, her iki veri setinin de net aykırı değerlere sahip olmadığı anlamına geliyor.

Ek kaynaklar

Excel’de Kutu Grafikleri Nasıl Oluşturulur ve Yorumlanır
SPSS’de Kutu Grafikleri Nasıl Oluşturulur ve Yorumlanır
R’de Çoklu Kutu Grafiği Nasıl Oluşturulur
Stata’da Kutu Grafikleri Nasıl Oluşturulur ve Yorumlanır