Regresyon analizinde kukla değişkenler nasıl kullanılır?

Doğrusal regresyon, bir veya daha fazla öngörücü değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullanabileceğimiz bir yöntemdir.

Genellikle niceliksel değişkenlerle doğrusal regresyon kullanırız. Bazen “sayısal” değişkenler olarak da adlandırılan bunlar ölçülebilir bir miktarı temsil eden değişkenlerdir. Örnekler şunları içerir:

• Bir evin metrekare sayısı
• Bir şehrin nüfus büyüklüğü
• Bir bireyin yaşı

Ancak bazen kategorik değişkenleri yordayıcı değişken olarak kullanmak isteriz. Bunlar adları veya etiketleri alan ve kategorilere ayrılabilen değişkenlerdir. Örnekler şunları içerir:

• Göz rengi (örneğin “mavi”, “yeşil”, “kahverengi”)
• Cinsiyet (örneğin “erkek”, “kadın”)
• Medeni durum (örneğin “evli”, “bekar”, “boşanmış”)

Kategorik değişkenler kullanılırken “mavi”, “yeşil”, “kahverengi” gibi değerlere sadece 1, 2, 3 gibi değerler atamak mantıklı değildir, çünkü bunu söylemek mantıklı değildir. o yeşil çifttir. Mavi veya kahverengi kadar renkli olan, maviden üç kat daha renklidir.

Bunun yerine çözüm kukla değişkenleri kullanmaktır. Bunlar regresyon analizi için özel olarak oluşturduğumuz ve iki değerden birini alan değişkenlerdir: sıfır veya bir.

Kukla değişkenler: Regresyon analizinde, iki değerden yalnızca birini alabilen kategorik verileri temsil etmek için kullanılan sayısal değişkenler: sıfır veya bir.

Oluşturmamız gereken kukla değişken sayısı k -1’e eşittir; burada k , kategorik değişkenin alabileceği farklı değerlerin sayısıdır.

Aşağıdaki örnekler, farklı veri kümeleri için kukla değişkenlerin nasıl oluşturulacağını göstermektedir.

Örnek 1: Yalnızca iki değere sahip bir kukla değişken oluşturun

Aşağıdaki veri setine sahip olduğumuzu ve geliri tahmin etmek için cinsiyet ve yaşı kullanmak istediğimizi varsayalım:

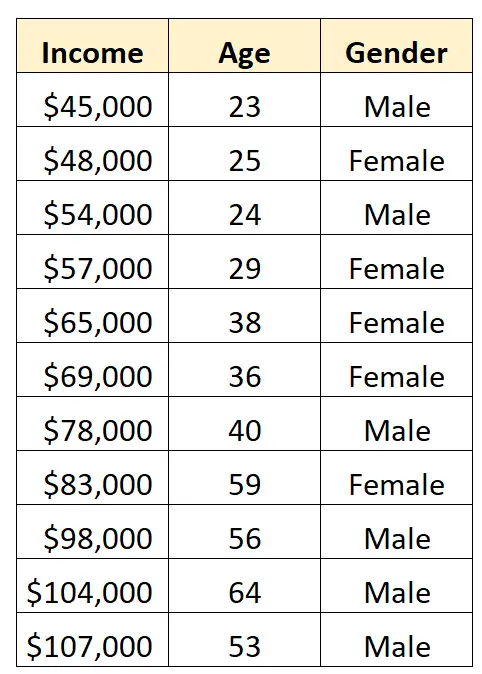
Cinsiyeti bir regresyon modelinde yordayıcı değişken olarak kullanmak için onu kukla değişkene dönüştürmemiz gerekir.

Bu şu anda iki farklı değer alabilen (“Erkek” veya “Kadın”) kategorik bir değişken olduğundan, basitçe k -1 = 2-1 = 1 kukla değişken oluşturuyoruz.

Bu kukla değişkeni oluşturmak için değerlerden birini (“Erkek” veya “Kadın”) 0’ı, diğerini ise 1’i temsil edecek şekilde seçebiliriz.

Genel olarak, genellikle bu veri kümesinde en sık görülen değeri “Erkek” olan 0 ile temsil ederiz.

Cinsiyeti yapay bir değişkene nasıl dönüştüreceğiniz aşağıda açıklanmıştır:

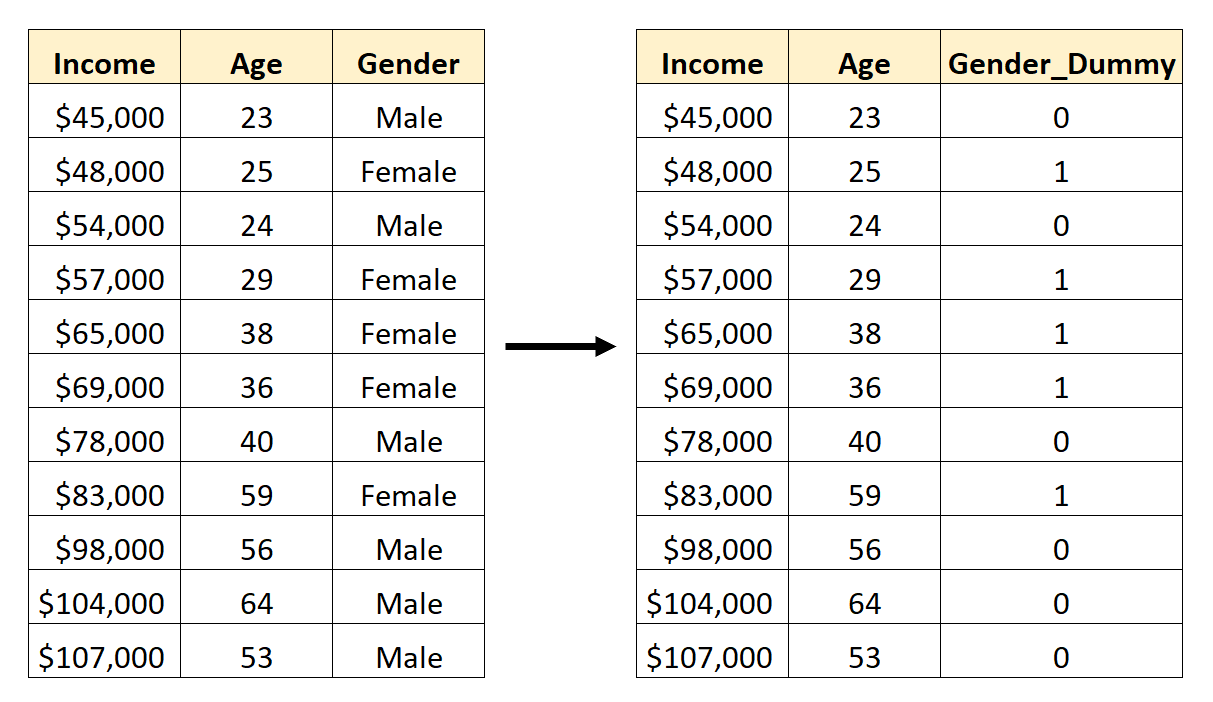
Daha sonra Yaş ve Gender_Dummy’yi bir regresyon modelinde yordayıcı değişkenler olarak kullanabiliriz.

Örnek 2: Birden çok değere sahip bir kukla değişken oluşturun

Diyelim ki aşağıdaki veri setine sahibiz ve geliri tahmin etmek için medeni durumu ve yaşı kullanmak istiyoruz:

Medeni durumu bir regresyon modelinde yordayıcı değişken olarak kullanmak için onu kukla değişkene dönüştürmemiz gerekir.

Bu şu anda üç farklı değer alabilen kategorik bir değişken olduğundan (“Bekar”, “Evli” veya “Boşanmış”) k -1 = 3-1 = 2 kukla değişken oluşturmamız gerekiyor.

Bu kukla değişkeni oluşturmak için, en sık göründüğü için temel değer olarak “Tek” bırakabiliriz. İşte medeni durumu kukla değişkenlere nasıl dönüştüreceğimiz:

Daha sonra bir regresyon modelinde Yaş , Evli ve Boşanmış’ı yordayıcı değişkenler olarak kullanabiliriz.

Regresyon çıktısının kukla değişkenlerle nasıl yorumlanacağı

Önceki örnekteki veri kümesini yordayıcı değişkenler olarak Yaş , Evli ve Boşanmış ve yanıt değişkeni olarak Gelir ile kullanarak çoklu doğrusal regresyon modeline uyduğumuzu varsayalım.

İşte regresyonun sonucu:

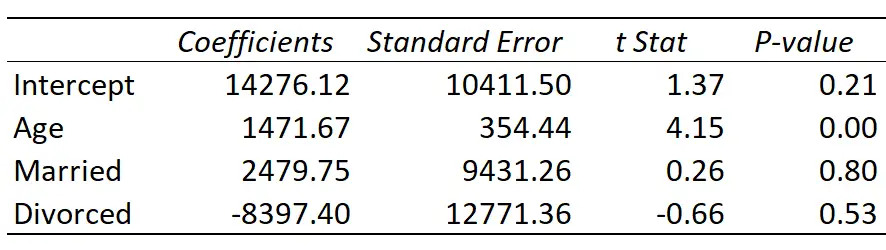
Uygun regresyon çizgisi şu şekilde tanımlanır:

Gelir = 14.276,21 + 1.471,67*(Yaş) + 2.479,75*(Evli) – 8.397,40*(Boşanmış)

Bir bireyin yaşına ve medeni durumuna göre tahmini gelirini bulmak için bu denklemi kullanabiliriz. Örneğin, 35 yaşında ve evli bir kişinin tahmini geliri 68.264 ABD Doları olacaktır:

Gelir = 14.276,21 + 1.471,67*(35) + 2.479,75*(1) – 8.397,40*(0) = 68.264 ABD doları

Tablodaki regresyon katsayılarını şu şekilde yorumlayabilirsiniz:

• Kesişme: Kesişme, sıfır yaşındaki tek bir kişinin ortalama gelirini temsil eder. Açıkçası sıfır yıla sahip olamazsınız, dolayısıyla bu özel regresyon modelinde kesişimi tek başına yorumlamanın bir anlamı yoktur.
• Yaş: Yaştaki her yıl artış, gelirde ortalama 1.471,67 dolarlık bir artışla ilişkilidir. P değeri (0,00) 0,05’ten küçük olduğundan yaş, gelirin istatistiksel olarak anlamlı bir yordayıcısıdır.
• Evli: Evli bir kişi, bekar bir kişiden ortalama 2.479,75 dolar daha fazla kazanıyor. P değeri (0,80) 0,05’ten küçük olmadığından bu fark istatistiksel olarak anlamlı değildir.
• Boşanmış: Boşanmış bir kişi, bekar bir kişiden ortalama 8.397,40 dolar daha az kazanıyor. P değeri (0,53) 0,05’ten küçük olmadığından bu fark istatistiksel olarak anlamlı değildir.

Her iki kukla değişken de istatistiksel olarak anlamlı olmadığından, gelire öngörücü bir değer katmadığı için medeni durumu bir yordayıcı olarak modelden çıkarabilirdik.

Ek kaynaklar

Niteliksel ve niceliksel değişkenler
Kukla değişken tuzağı
Regresyon Tablosu Nasıl Okunmalı ve Yorumlanmalı
P değerlerinin ve istatistiksel anlamlılığın açıklaması