R'de üstel regresyon (adım adım)

Üstel regresyon, aşağıdaki durumları modellemek için kullanılabilecek bir regresyon türüdür:

1. Üstel Büyüme: Büyüme yavaş başlar, daha sonra hızlı ve sınırsız bir şekilde hızlanır.

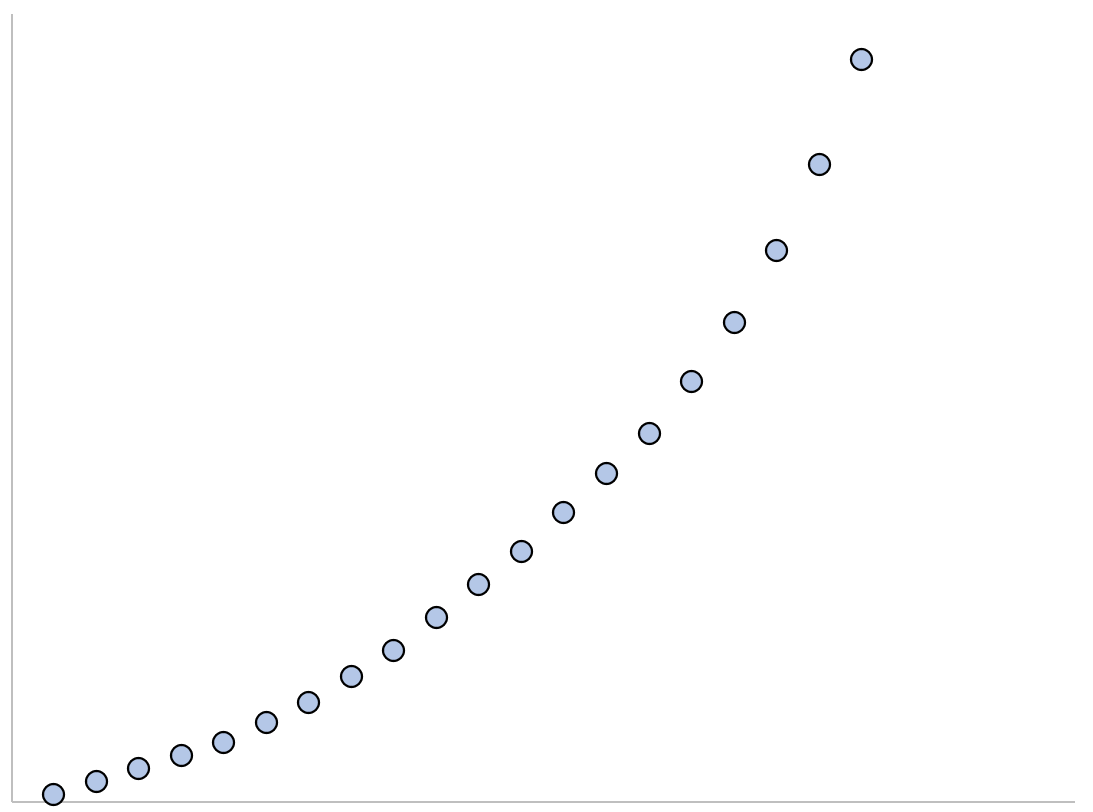
2. Üstel bozunma: Bozunma hızla başlar ve sonra yavaşlayarak sıfıra yaklaşır.

Üstel regresyon modelinin denklemi aşağıdaki formu alır:

y = ^abx

Altın:

• y: yanıt değişkeni
• x: tahmin değişkeni
• a, b: x ve y arasındaki ilişkiyi tanımlayan regresyon katsayıları

Aşağıdaki adım adım örnek, R’de üstel regresyonun nasıl gerçekleştirileceğini gösterir.

1. Adım: Verileri oluşturun

Öncelikle iki değişken için sahte veriler oluşturalım: x ve y :

 x=1:20
y=c(1, 3, 5, 7, 9, 12, 15, 19, 23, 28, 33, 38, 44, 50, 56, 64, 73, 84, 97, 113)

2. Adım: Verileri görselleştirin

Şimdi x ile y arasındaki ilişkiyi görselleştirmek için hızlı bir dağılım grafiği oluşturalım:

 plot(x, y) 

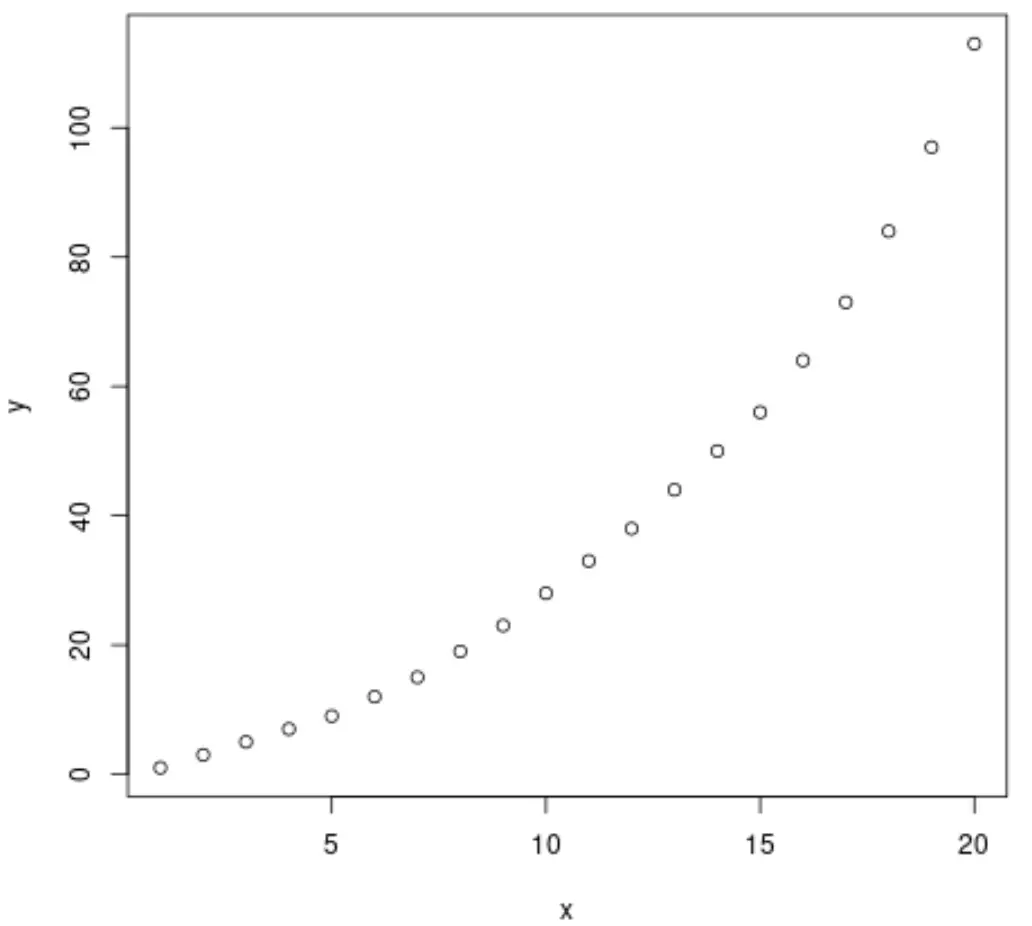
Grafikten iki değişken arasında net bir üstel büyüme modelinin olduğunu görebiliriz.

Bu nedenle değişkenler arasındaki ilişkiyi tanımlamak için üstel bir regresyon denklemi uydurmak akıllıca görünmektedir.

Adım 3: Üstel regresyon modelini yerleştirin

Daha sonra, yanıt değişkeni olarak y’nin ve tahmin değişkeni olarak x’in doğal logaritmasını kullanarak üstel bir regresyon modeline uyum sağlamak için lm() işlevini kullanacağız:

 #fit the model
model <- lm( log (y) ~ x)

#view the output of the model
summary(model)

Call:
lm(formula = log(y) ~ x)

Residuals:
    Min 1Q Median 3Q Max 
-1.1858 -0.1768 0.1104 0.2720 0.3300 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.98166 0.17118 5.735 1.95e-05 ***
x 0.20410 0.01429 14.283 2.92e-11 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3685 on 18 degrees of freedom
Multiple R-squared: 0.9189, Adjusted R-squared: 0.9144 
F-statistic: 204 on 1 and 18 DF, p-value: 2.917e-11

Modelin genel F değeri 204’tür ve buna karşılık gelen p değeri son derece düşüktür (2,917e-11), bu da modelin bir bütün olarak faydalı olduğunu göstermektedir.

Çıktı tablosundaki katsayıları kullanarak, uygun üstel regresyon denkleminin şöyle olduğunu görebiliriz:

ln(y) = 0,9817 + 0,2041(x)

Her iki tarafa da e uygulandığında denklemi aşağıdaki gibi yeniden yazabiliriz:

y = 2,6689 * ^1,2264x

Bu denklemi, tahmin değişkeni x’in değerine dayanarak yanıt değişkeni y’yi tahmin etmek için kullanabiliriz. Örneğin, x = 12 ise y’nin 30,897 olacağını tahmin ederiz:

y = 2,6689 * 1,2264 ¹² = 30,897

Bonus: Belirli bir tahminci ve yanıt değişkeni için üstel regresyon denklemini otomatik olarak hesaplamak için bu çevrimiçi üstel regresyon hesaplayıcısını kullanmaktan çekinmeyin.

Ek kaynaklar

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de ikinci dereceden regresyon nasıl gerçekleştirilir?
R’de polinom regresyonu nasıl gerçekleştirilir