Karelerin toplamına i̇lişkin nazik bir kılavuz: sst, ssr, sse
Doğrusal regresyon, bir veri kümesine en iyi “uyan” çizgiyi bulmak için kullanılır.
Regresyon çizgisinin verilere gerçekte ne kadar iyi uyduğunu ölçmek için sıklıkla üç farklı kareler toplamı değeri kullanırız:
1. Toplam Karelerin Toplamı (SST) – Bireysel veri noktaları (y i ) ile yanıt değişkeninin ortalaması ( y ) arasındaki farkların karelerinin toplamı.
- SST = Σ(y ben – y ) 2
2. Karelerin Toplamı Regresyon (SSR) – Tahmin edilen veri noktaları (ŷ i ) ile yanıt değişkeninin ortalaması ( y ) arasındaki farkların karelerinin toplamı.
- SSR = Σ(ŷ ben – y ) 2
3. Kareler Toplamı Hatası (SSE) – Tahmin edilen veri noktaları (ŷ i ) ile gözlemlenen veri noktaları (y i ) arasındaki farkların karelerinin toplamı.
- SSE = Σ(ŷ ben – y ben ) 2
Bu üç önlem arasında aşağıdaki ilişki vardır:
SST = SSR + SSE
Yani bu ölçümlerden ikisini biliyorsak üçüncüyü hesaplamak için basit cebir kullanabiliriz.
SSR, SST ve R-Kare
Bazen belirleme katsayısı olarak da adlandırılan R-kare , doğrusal bir regresyon modelinin bir veri kümesine ne kadar iyi uyduğunun bir ölçüsüdür. Yanıt değişkenindeki, yordayıcı değişken tarafından açıklanabilen varyansın oranını temsil eder.
R-kare değeri 0 ila 1 arasında değişebilir. 0 değeri, yanıt değişkeninin yordayıcı değişken tarafından hiçbir şekilde açıklanamayacağını gösterir. 1 değeri, yanıt değişkeninin yordayıcı değişken tarafından hatasız olarak mükemmel bir şekilde açıklanabileceğini gösterir.
SSR ve SST’yi kullanarak R kareyi şu şekilde hesaplayabiliriz:
R kare = SSR / SST
Örneğin, belirli bir regresyon modeli için SSR 137,5 ve SST 156 ise R kareyi şu şekilde hesaplarız:
R kare = 137,5 / 156 = 0,8814
Bu bize yanıt değişkenindeki değişimin %88,14’ünün yordayıcı değişken tarafından açıklanabileceğini göstermektedir.
SST, SSR, SSE’yi hesaplayın: adım adım örnek
Altı farklı öğrencinin okuduğu saat sayısını ve final sınav puanlarını gösteren aşağıdaki veri setine sahip olduğumuzu varsayalım:
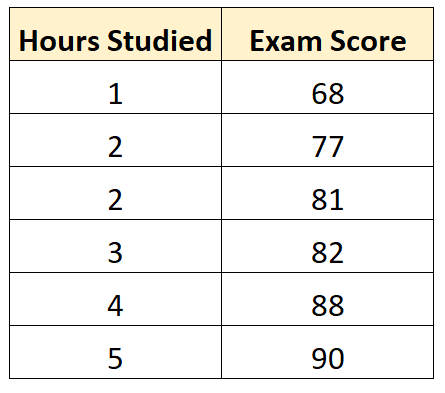
Bazı istatistiksel yazılımları ( R , Excel , Python gibi) veya hatta elle kullanarak, en uygun çizginin şöyle olduğunu görebiliriz:
Puan = 66,615 + 5,0769*(Saat)
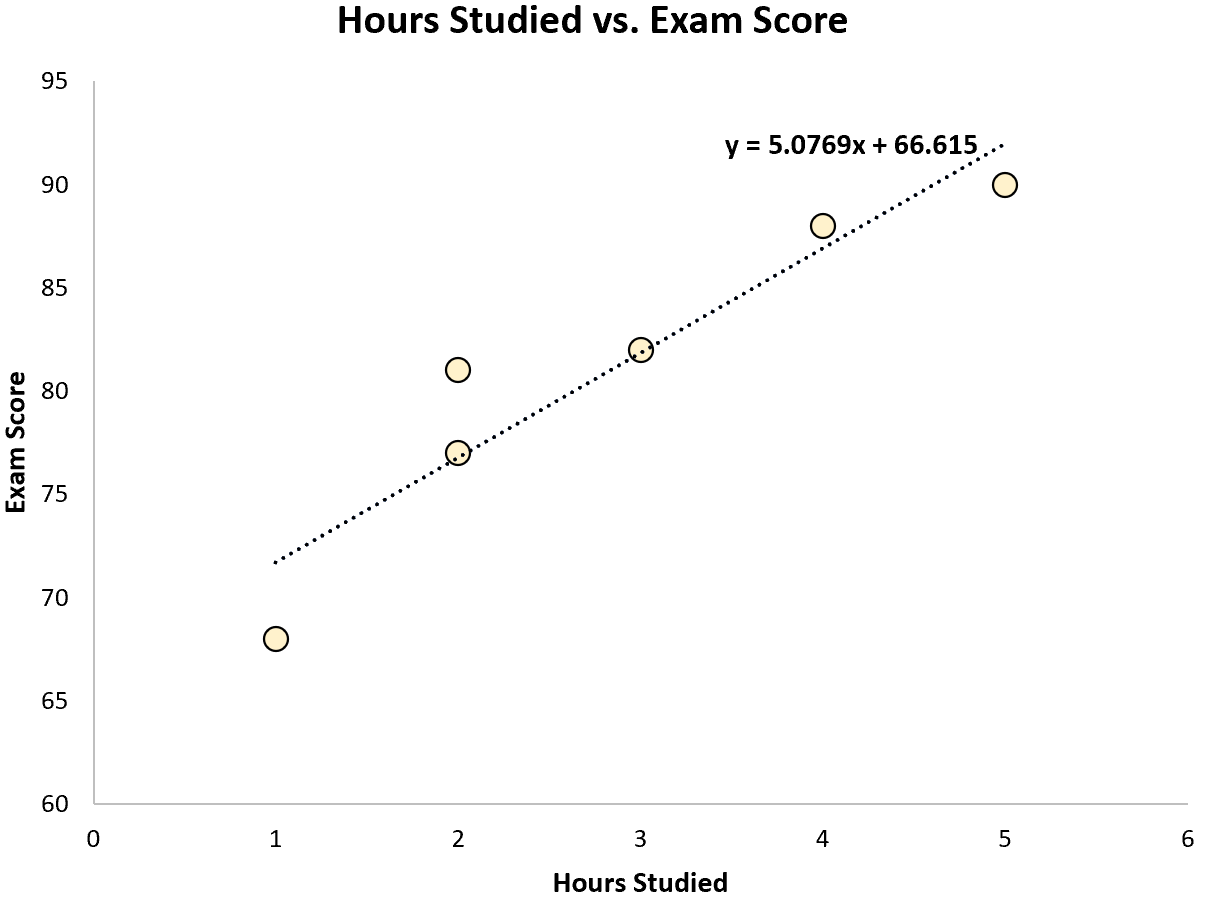
En uygun denklemin doğrusunu öğrendikten sonra SST, SSR ve SSE’yi hesaplamak için aşağıdaki adımları kullanabiliriz:
Adım 1: Yanıt değişkeninin ortalamasını hesaplayın.
Yanıt değişkeninin ( y ) ortalaması 81 olarak ortaya çıkıyor.
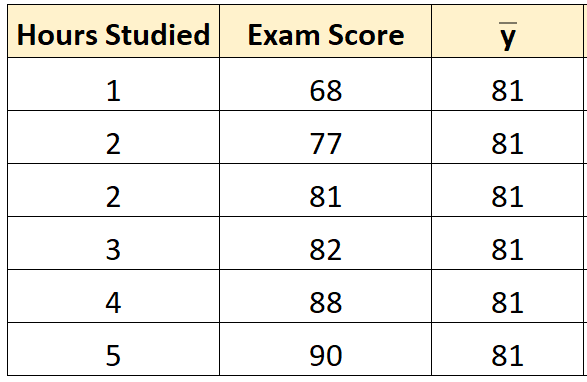
Adım 2: Her gözlem için tahmin edilen değeri hesaplayın.
Daha sonra her öğrenci için öngörülen sınav puanını () hesaplamak için en uygun denklem satırını kullanabiliriz.
Örneğin bir saat ders çalışan öğrenci için öngörülen sınav notu şöyledir:
Puan = 66,615 + 5,0769*(1) = 71,69 .
Her öğrenci için tahmin edilen puanı bulmak için aynı yaklaşımı kullanabiliriz:
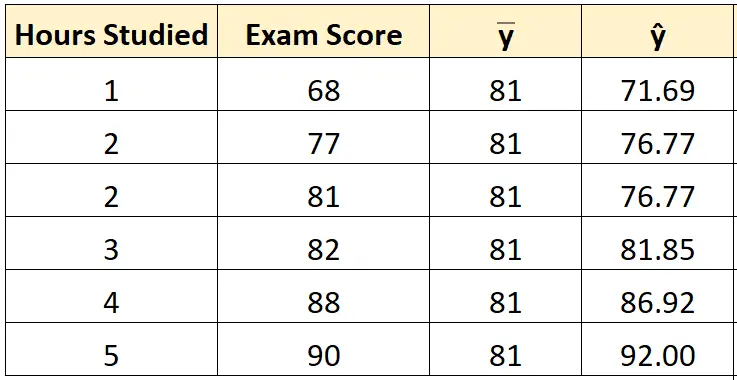
Adım 3: Toplam kareler toplamını (SST) hesaplayın.
Daha sonra toplam karelerin toplamını hesaplayabiliriz.
Örneğin, ilk öğrenci için karelerin toplamı şu şekildedir:
(y ben – y ) 2 = (68 – 81) 2 = 169 .
Her öğrencinin karelerinin toplamını bulmak için aynı yaklaşımı kullanabiliriz:
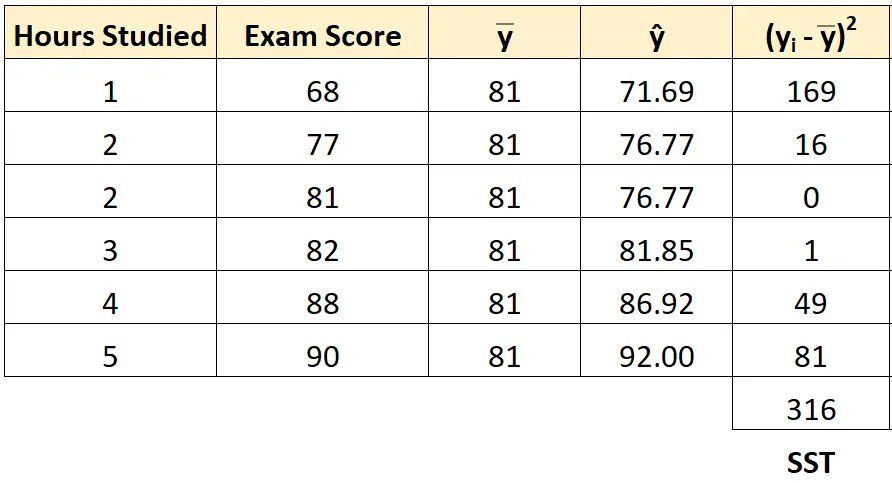
Toplam kareler toplamı 316 çıkıyor.
Adım 4: Kareler toplamı regresyonunu (SSR) hesaplayın.
Daha sonra kareler toplamı regresyonunu hesaplayabiliriz.
Örneğin, birinci öğrenci için kareler toplamı regresyonu şöyledir:
( ŷi – y ) 2 = (71,69 – 81) 2 = 86,64 .
Her öğrenci için kareler toplamının regresyonunu bulmak için aynı yaklaşımı kullanabiliriz:
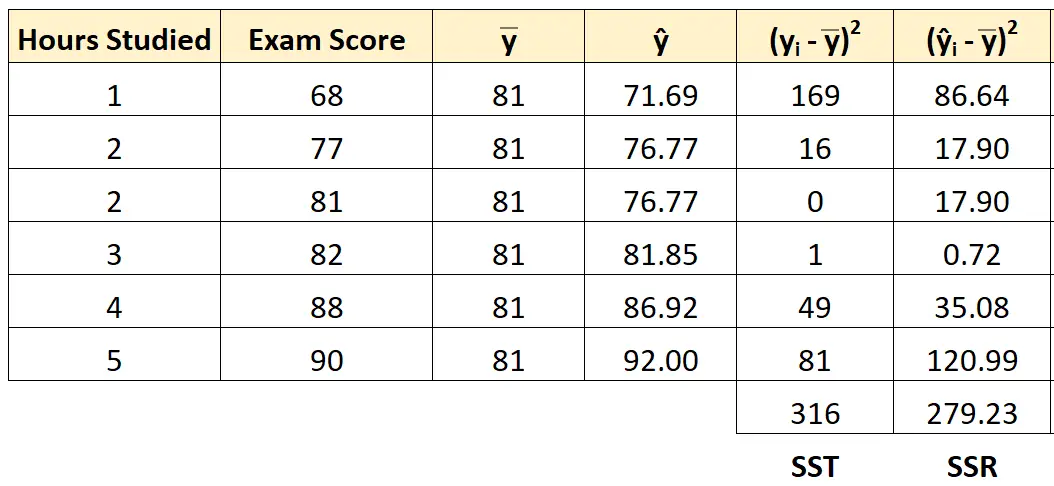
Kareler toplamı regresyonu 279,23 olarak çıkıyor.
Adım 5: Kareler toplamı hatasının (SSE) hesaplanması.
Daha sonra kareler toplamının hatasını hesaplayabiliriz.
Örneğin, birinci öğrencinin kareler toplamı hatası şöyledir:
(ŷ ben – y ben ) 2 = (71,69 – 68) 2 = 13,63 .
Her öğrenci için hatanın karelerinin toplamını bulmak için aynı yaklaşımı kullanabiliriz:
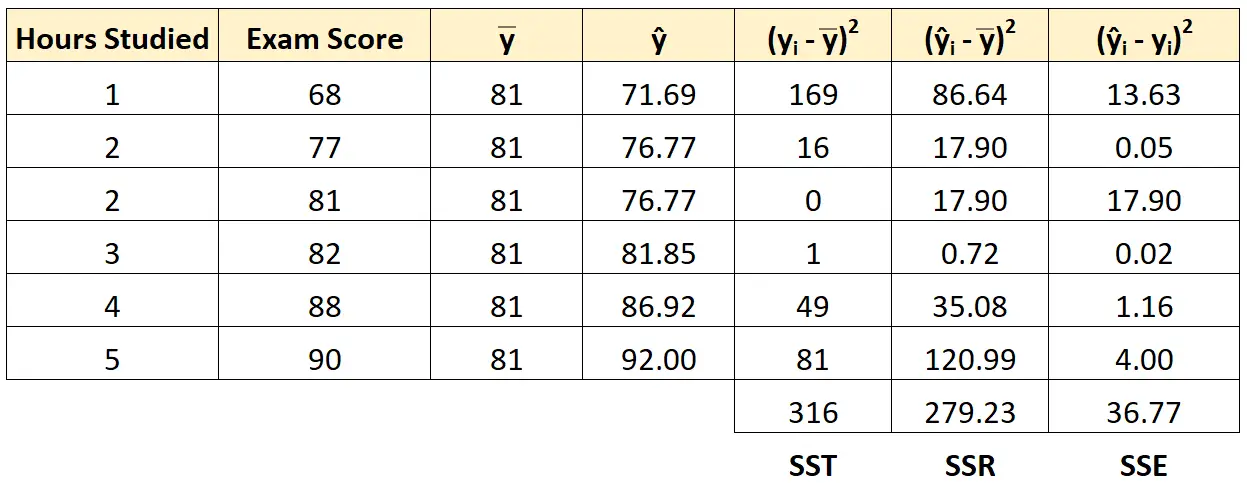
SST = SSR + SSE olduğunu doğrulayabiliriz
- SST = SSR + SSE
- 316 = 279,23 + 36,77
Regresyon modelinin R karesini aşağıdaki denklemi kullanarak da hesaplayabiliriz:
- R kare = SSR / SST
- R kare = 279,23 / 316
- R kare = 0,8836
Bu bize sınav puanlarındaki farklılığın %88,36’sının çalışılan saat sayısıyla açıklanabileceğini söylüyor.
Ek kaynaklar
Herhangi bir basit doğrusal regresyon çizgisi için SST, SSR ve SSE’yi otomatik olarak hesaplamak amacıyla aşağıdaki hesaplayıcıları kullanabilirsiniz:
SST hesaplayıcı
RSS hesaplayıcı
ESS hesaplayıcı
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil