Tek değişkenli analiz nedir? (tanım & #038; örnek)
Tek değişkenli analiz terimi, bir değişkenin analizini ifade eder. Bunu “uni” ön ekinin “bir” anlamına gelmesinden dolayı hatırlayabilirsiniz.
Tek değişkenli analizin amacı, tek bir değişkene ilişkin değerlerin dağılımını anlamaktır. Bu analiz türünü aşağıdakilerle karşılaştırabilirsiniz:
- İki değişkenli analiz : İki değişkenin analizi.
- Çok değişkenli analiz: İki veya daha fazla değişkenin analizi.
Örneğin aşağıdaki veri setine sahip olduğumuzu varsayalım:
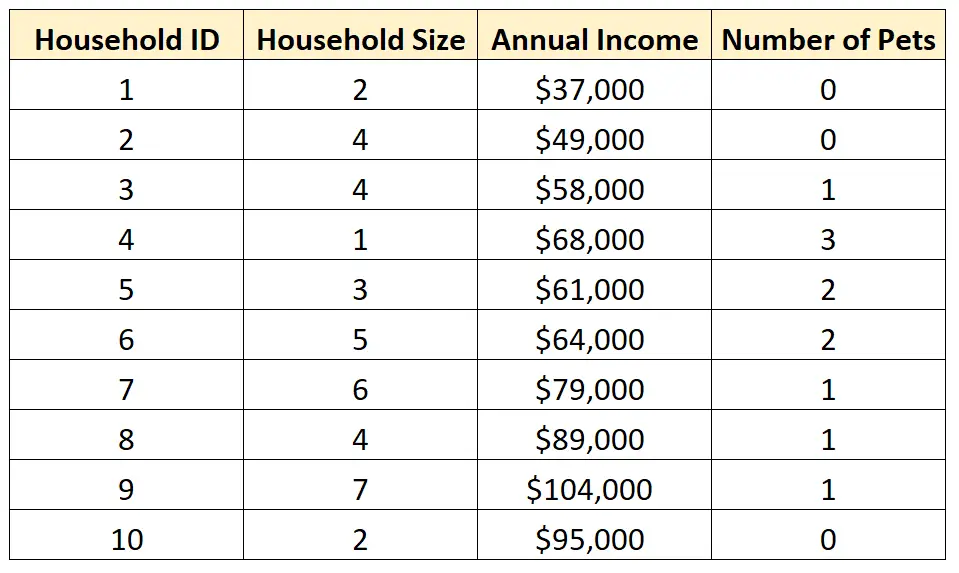
Değer dağılımını daha iyi anlamak için veri kümesindeki bireysel değişkenlerden biri üzerinde tek değişkenli bir analiz yapmayı seçebiliriz.
Örneğin, Hane büyüklüğü değişkeni üzerinde tek değişkenli bir analiz yapmayı seçebiliriz:
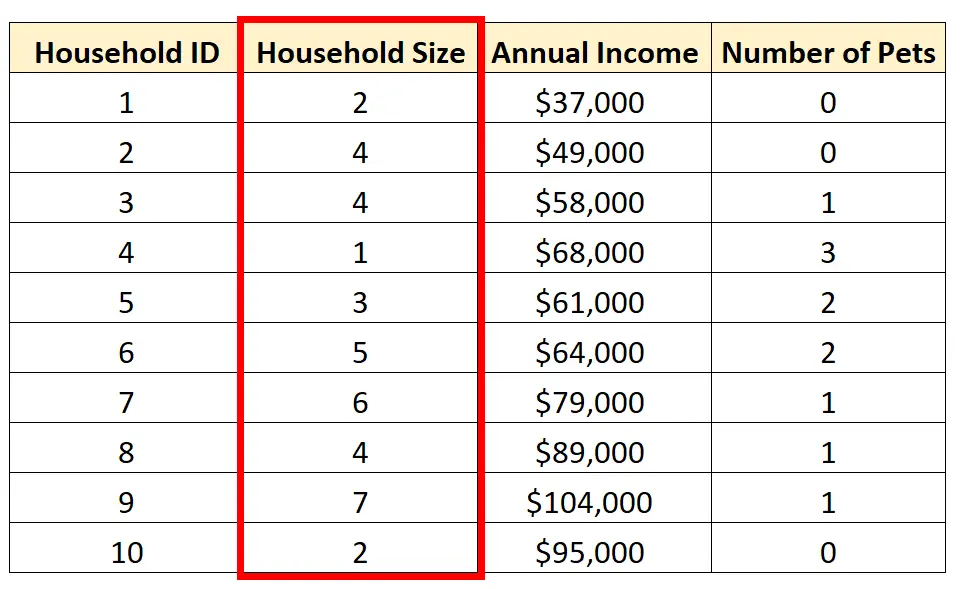
Tek değişkenli analiz gerçekleştirmenin üç yaygın yolu vardır:
1. Özet istatistikler
Tek değişkenli analiz gerçekleştirmenin en yaygın yolu, bir değişkeni özet istatistikler kullanarak tanımlamaktır.
İki yaygın özet istatistik türü vardır:
- Merkezi eğilim ölçüleri : Bu sayılar bir veri kümesinin merkezinin nerede olduğunu tanımlar. Örnekler arasında ortalama ve medyan yer alır.
- Dağılım ölçüleri : Bu sayılar veri setindeki değerlerin dağılımını tanımlar. Örnekler arasında aralık , çeyrekler arası aralık , standart sapma ve varyans yer alır.
2. Frekans dağılımları
Tek değişkenli analiz gerçekleştirmenin bir başka yolu da, bir veri kümesinde farklı değerlerin ne sıklıkta göründüğünü açıklayan bir frekans dağılımı oluşturmaktır.
3. Grafikler
Tek değişkenli analiz gerçekleştirmenin bir başka yolu da belirli bir değişkene ilişkin değerlerin dağılımını görselleştirmek için grafikler oluşturmaktır.
Yaygın örnekler şunları içerir:
- Kutu grafikleri
- Histogramlar
- Yoğunluk eğrileri
- Camembert’ler
Aşağıdaki örnekler, daha önce bahsettiğimiz veri setimizdeki Hane Boyutu değişkenini kullanarak her tür tek değişkenli analizin nasıl gerçekleştirileceğini göstermektedir:

Özet istatistikler
Hanehalkı büyüklüğünün merkezi eğilim ölçülerini aşağıdaki şekilde hesaplayabiliriz:
- Ortalama (ortalama değer): 3,8
- Medyan (ortalama değer): 4
Bu değerler bize “merkezi” değerin nerede olduğu konusunda fikir veriyor.
Ayrıca aşağıdaki dağılım ölçülerini de hesaplayabiliriz:
- Aralık (maks. ve min. arasındaki fark): 6
- Çeyrekler arası ölçek (değerlerin ortadaki %50’sinin dağılımı): 2,5
- Standart sapma (ortalama yayılma ölçüsü): 1,87
Bu değerler bize bu değişkenin değerlerinin dağılımı hakkında fikir vermektedir.
Frekans dağılımı
Farklı değerlerin ne sıklıkta ortaya çıktığını özetlemek için aşağıdaki frekans dağılım tablosunu da oluşturabiliriz:
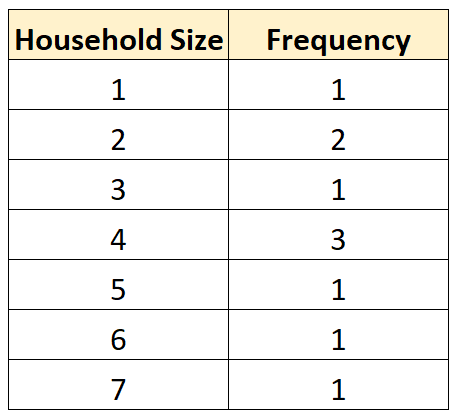
Bu da en yaygın hane büyüklüğünün 4 kişi olduğunu hızlı bir şekilde görmemizi sağlıyor.
Kaynak: Herhangi bir değişken için otomatik olarak bir frekans dağılımı oluşturmak amacıyla bu frekans hesaplayıcıyı kullanabilirsiniz.
Grafik
Hanehalkı büyüklüğüne göre değerlerin dağılımını görselleştirmemize yardımcı olması için aşağıdaki grafikleri oluşturabiliriz:
1. Kutu grafiği
Kutu grafiği , bir veri kümesinin beş basamaklı özetini gösteren bir grafiktir.
Beş rakamlı özet şunları içerir:
- Asgari değer
- İlk çeyrek
- Medyan değer
- Üçüncü çeyrek
- Maksimum değer
Hane Boyutu değişkeni için bir kutu grafiği şöyle görünecektir:
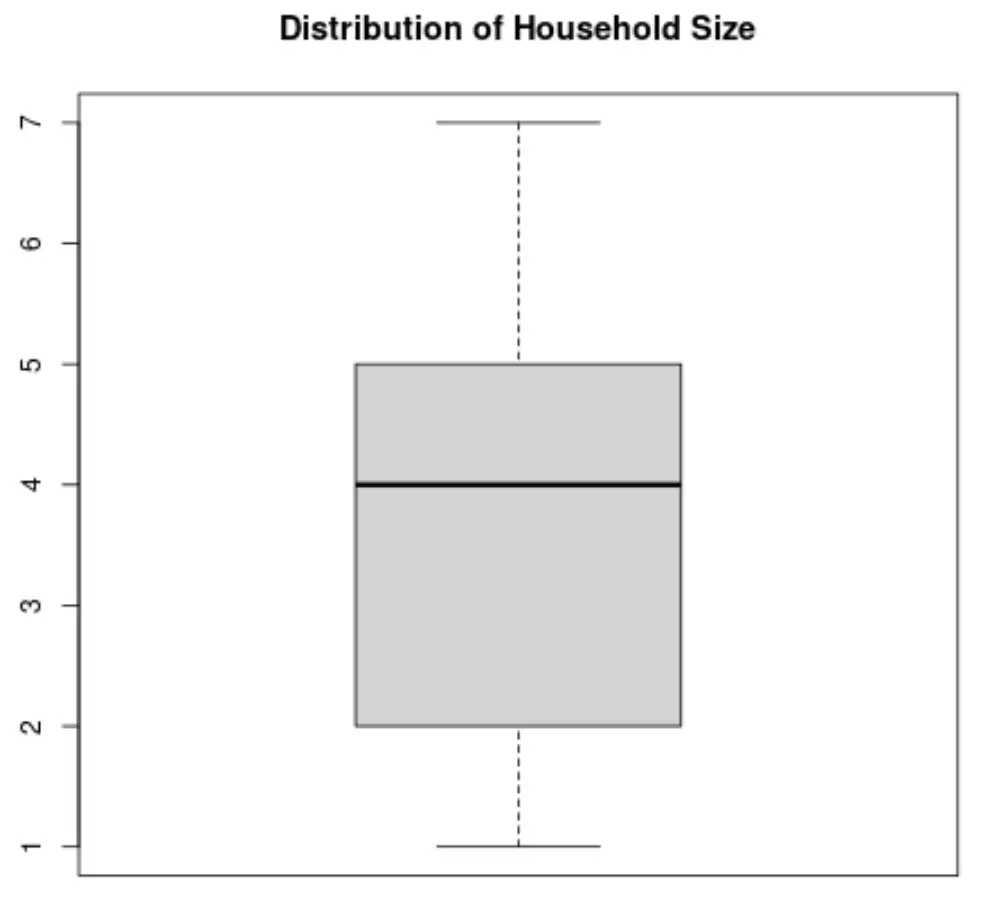
Kaynak: Bu kutu grafiği oluşturucuyu, herhangi bir değişken için otomatik olarak bir kutu grafiği oluşturmak için kullanabilirsiniz.
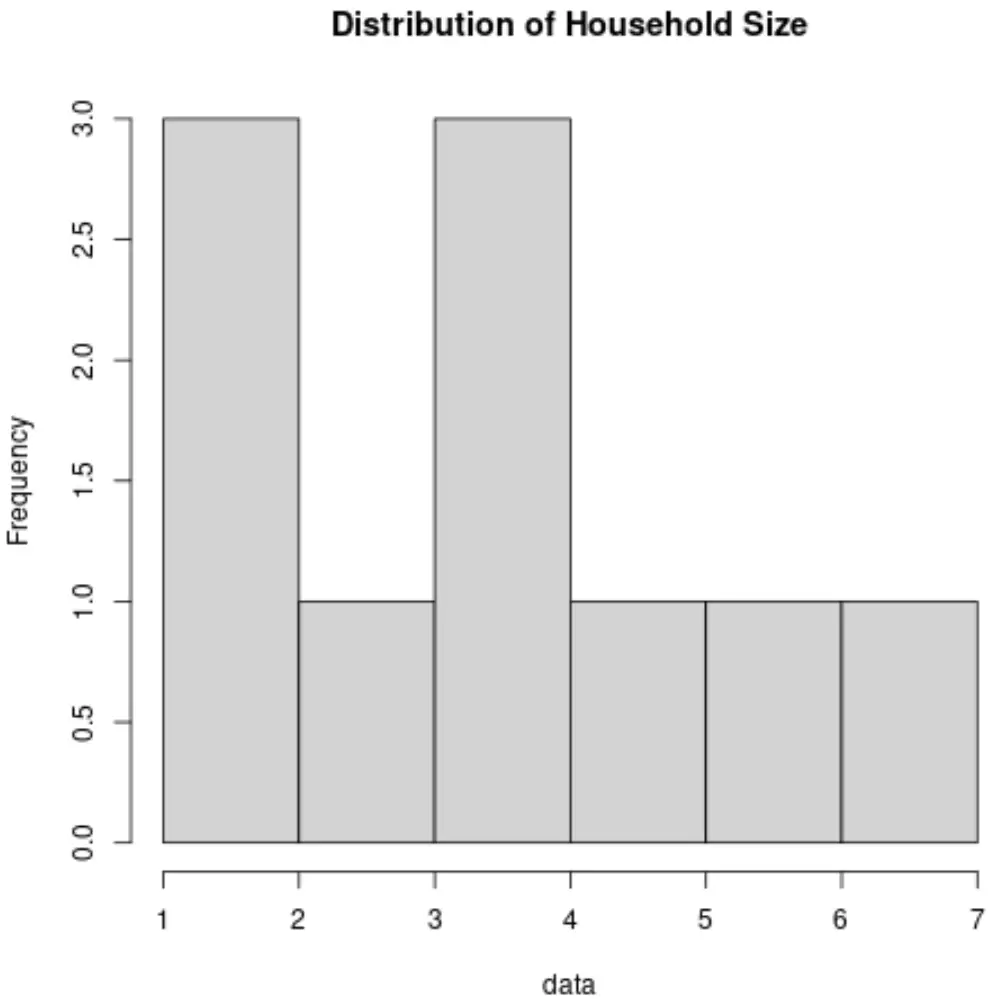
2. Histogram
Histogram, frekansları görüntülemek için dikey çubuklar kullanan bir grafik türüdür. Bu grafik türü, bir veri kümesindeki değerlerin dağılımını görselleştirmenin yararlı bir yoludur.
Hane Boyutu değişkeni için bir histogram şu şekilde görünecektir:
3. Yoğunluk eğrisi
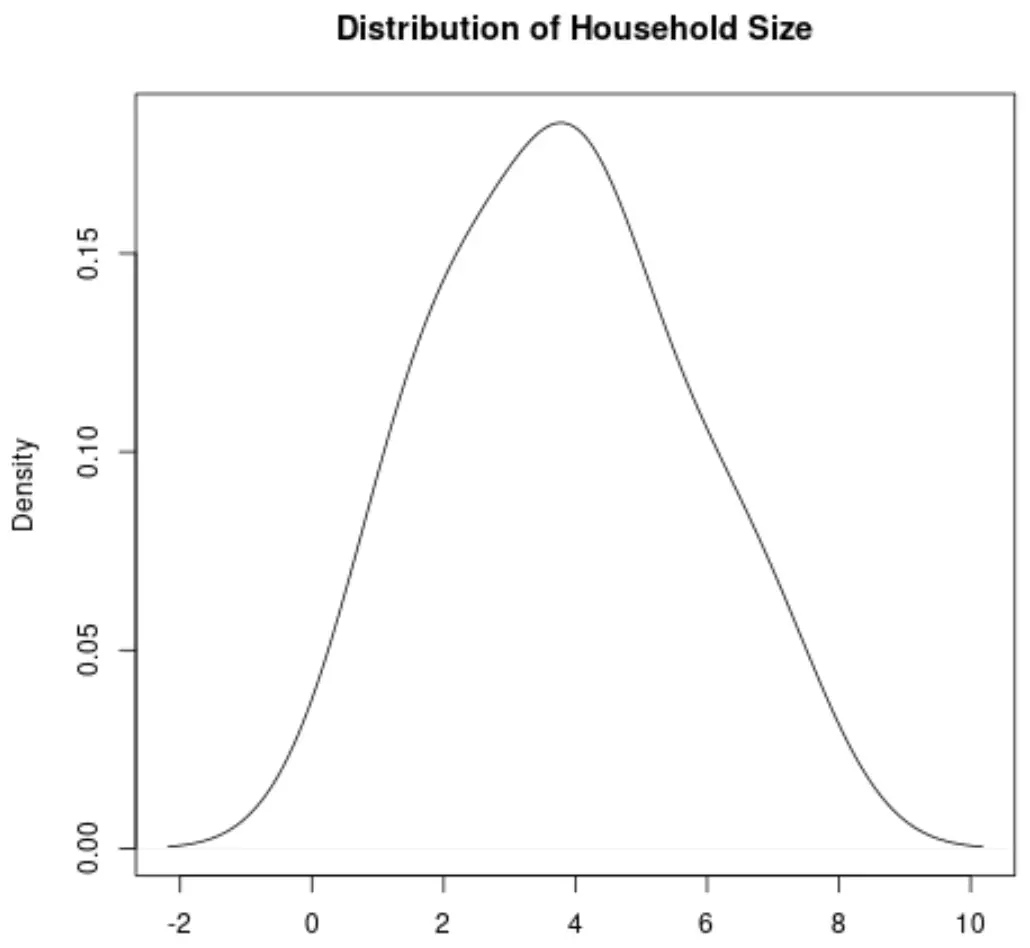
Yoğunluk eğrisi, bir veri kümesindeki değerlerin dağılımını temsil eden bir grafik üzerindeki eğridir.
Bir dağılımın sık görülen değerlerin bir veya daha fazla “zirvesine” sahip olup olmadığı ve dağılımın sola veya sağa çarpık olup olmadığı da dahil olmak üzere, bir dağılımın “şeklini” görselleştirmek için özellikle kullanışlıdır.
Hanehalkı Büyüklüğü değişkenine ilişkin yoğunluk eğrisi şu şekilde görünecektir:
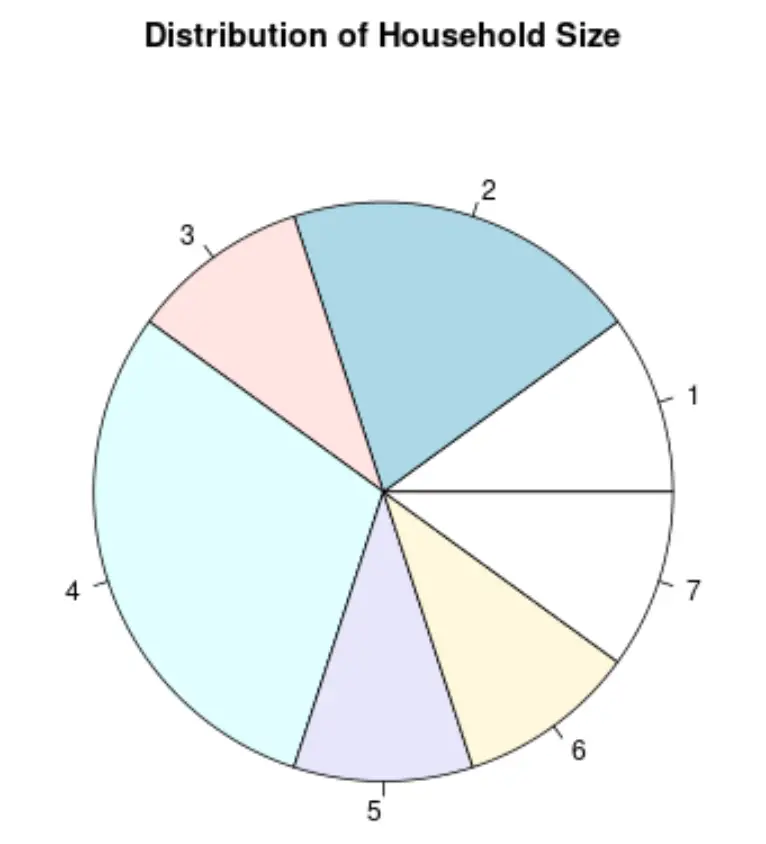
4. Pasta grafiği
Pasta grafik, daire şeklindeki bir grafik türüdür ve bir bütünün oranlarını temsil etmek için dilimler kullanır.
Hane Boyutu değişkeni için pasta grafiği şu şekilde görünecektir:
Veri türüne bağlı olarak değerlerin dağılımını görselleştirmek için bu grafiklerden biri diğerlerinden daha kullanışlı olabilir.