Kümülatif bağıl frekans

Bu makalede istatistiklerde kümülatif göreli frekansın ne olduğu açıklanmaktadır. Böylece kümülatif bağıl frekansın tanımını, kümülatif bağıl frekansın nasıl elde edileceğini ve adım adım çözülen iki alıştırmayı bulacaksınız.

Kümülatif bağıl frekans nedir?

İstatistikte kümülatif göreceli frekans , göreceli frekansların kümülatif toplamıdır. Yani, bir değerin kümülatif bağıl frekansı, o değerin bağıl frekansı artı ondan küçük tüm değerlerin bağıl frekanslarının toplamına eşittir.

Kümülatif bağıl frekansın sembolü H _i’dir . Ancak istatistiklerde bu tür frekansın sembolüyle ilgili henüz tam bir fikir birliği yoktur, bu nedenle başka bir sembol kullanılarak da ifade edildiğini görebilirsiniz.

Açıkçası, kümülatif göreceli frekansın anlamını anlamak için öncelikle göreceli frekans kavramını net bir şekilde anlamanız gerekir, bu nedenle açıklamaya devam etmeden önce aşağıdaki bağlantıyı ziyaret etmenizi öneririm:

Kümülatif bağıl frekans nasıl hesaplanır?

Kümülatif bağıl frekansı hesaplamak için aşağıdaki adımlar izlenmelidir:

1. İstatistiksel örnekteki tüm farklı değerleri içeren bir frekans tablosu oluşturun.
2. Her değerin mutlak frekansını hesaplayın.
3. Mutlak frekanslardan her değerin bağıl frekansını belirleyin.
4. Her bir değerin kümülatif göreli frekansını bulun; bu frekans, değerin kendisinin göreli frekansı artı tüm küçük değerlerin göreli frekansları toplanarak hesaplanır.

Kümülatif bağıl frekans yüzdesini yani yüzde olarak ifade edilen kümülatif bağıl frekansı hesaplamak istiyorsanız aynı adımları izleyip sonuçları 100 ile çarpmanız gerektiğini unutmayın.

Kümülatif Göreli Frekans Örnekleri

Kümülatif bağıl frekansın nasıl hesaplandığını görebilmeniz için aşağıda adım adım çözülen iki örnek gösterilmektedir. İlk örnekte ayrık bir değişkenin kümülatif bağıl frekansını, ikinci örnekte ise süreç biraz değiştiği için sürekli bir değişkeni buluyoruz.

Örnek 1: ayrık değişken

• 30 kişilik bir sınıfta istatistik konusunda alınan notlar aşağıdaki gibidir. Her notanın kümülatif bağıl frekansı nedir?

Bu durumda değişken ondalık değer alamadığı için ayrıktır. Bu nedenle verileri aralıklara göre gruplamaya gerek yoktur ancak hesaplamalar doğrudan yapılabilir.

Böylece bir frekans tablosu hazırlıyor ve her farklı değerin mutlak frekansını belirliyoruz:

Daha sonra, her değerin göreceli sıklığını hesaplıyoruz (bunun nasıl yapıldığını yazının başındaki bağlantıda görebilirsiniz).

Veri setinin mutlak frekansını ve bağıl frekansını hesapladıktan sonra kümülatif bağıl frekansı elde edebiliriz. Bunu yapmak için, söz konusu değerin göreceli frekansını artı önceki tüm göreceli frekansları veya başka bir deyişle önceki birikmiş göreceli frekansı eklemeliyiz:

Kısaca mutlak frekans, bağıl frekans ve kümülatif bağıl frekansın yer aldığı frekans tablosu şu şekildedir:

Kümülatif bağıl frekansın son değerinin her zaman 1 olması gerektiğini unutmayın. Başka bir sayı alırsanız hesaplamalarda hata yapmışsınız demektir.

Örnek 2: sürekli değişken

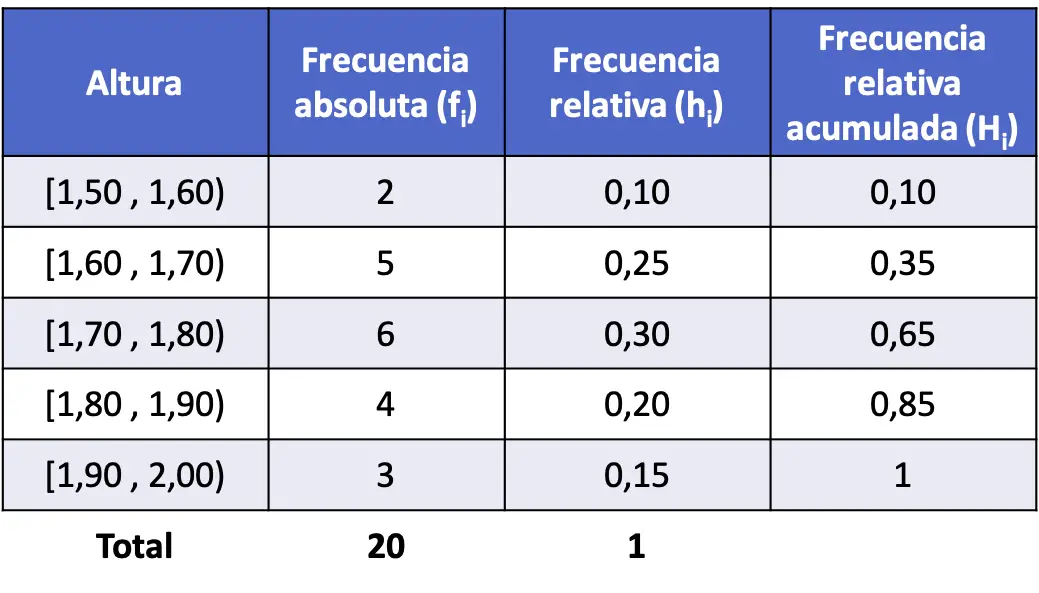
• 20 kişinin boyu ölçüldü ve aşağıda belirtilen sonuçlar elde edildi. Verileri aralıklara ayırın ve her aralığın kümülatif bağıl frekansını bulun.

Bu durum önceki problemden farklıdır çünkü sayılar ondalıktır, yani değişken herhangi bir değeri alabilir ve dolayısıyla süreklidir. Bu nedenle verileri aralıklara gruplayarak frekans tablosunu oluşturacağız.

Bu nedenle tabloyu oluştururuz ve her aralığın mutlak frekansını elde ederiz:

Artık her aralığın mutlak frekansını toplam veri noktası sayısına bölerek göreceli frekansları hesaplıyoruz:

Ve son olarak tüm aralıkların kümülatif bağıl frekanslarını buluyoruz. Daha önce olduğu gibi, bir aralığın kümülatif bağıl frekansını belirlemek için, söz konusu aralığın bağıl frekansı artı önceki bağıl frekansları toplamak gerekir:

Kümülatif bağıl frekans ve kümülatif mutlak frekans

Az önce kümülatif bağıl frekansın bağıl frekanstan nasıl türetildiğini gördük. Ancak bu tip frekans kümülatif mutlak frekans kullanılarak da bulunabilir.

Kümülatif bağıl frekans, kümülatif mutlak frekansın örnekteki toplam veri sayısına bölünmesiyle hesaplanabilir.

Bu nedenle kümülatif bağıl frekans formülü şu şekildedir:

Altın:

• 

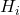
  kümülatif bağıl frekanstır.

• 

  birikmiş mutlak frekanstır .

• 

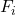
  toplam veri sayısıdır.

Yukarıda geliştirilen ilk örneği takip ederek, birikmiş mutlak frekanstan birikmiş bağıl frekansın nasıl bulunduğunu burada bulabilirsiniz:

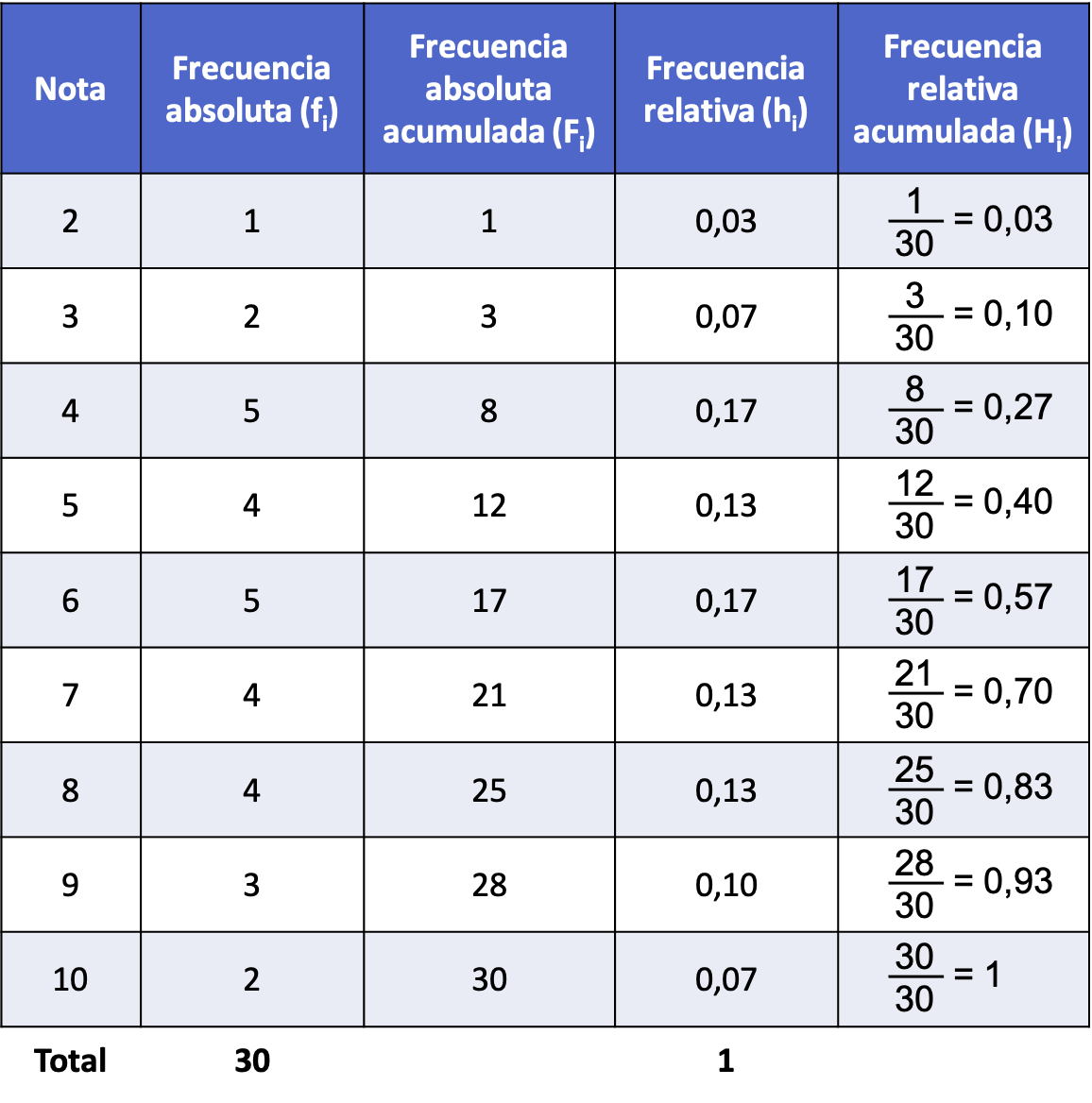
Yukarıdaki tablo tüm istatistiksel frekans türlerini içerdiğinden frekans tablosu olarak adlandırılmaktadır. Daha fazlasını öğrenmek için burayı tıklayın: