Normal dağılım ve standart normal dağılım: fark

Normal dağılım istatistikte en sık kullanılan olasılık dağılımıdır.

Aşağıdaki özelliklere sahiptir:

• Simetrik
• Çan şeklinde
• Ortalama ve medyan eşittir; her ikisi de dağıtımın merkezinde yer alır

Normal dağılımın ortalaması yerini, standart sapması ise yayılmasını belirler.

Örneğin, aşağıdaki grafik farklı ortalamalara ve standart sapmalara sahip üç normal dağılımı göstermektedir:

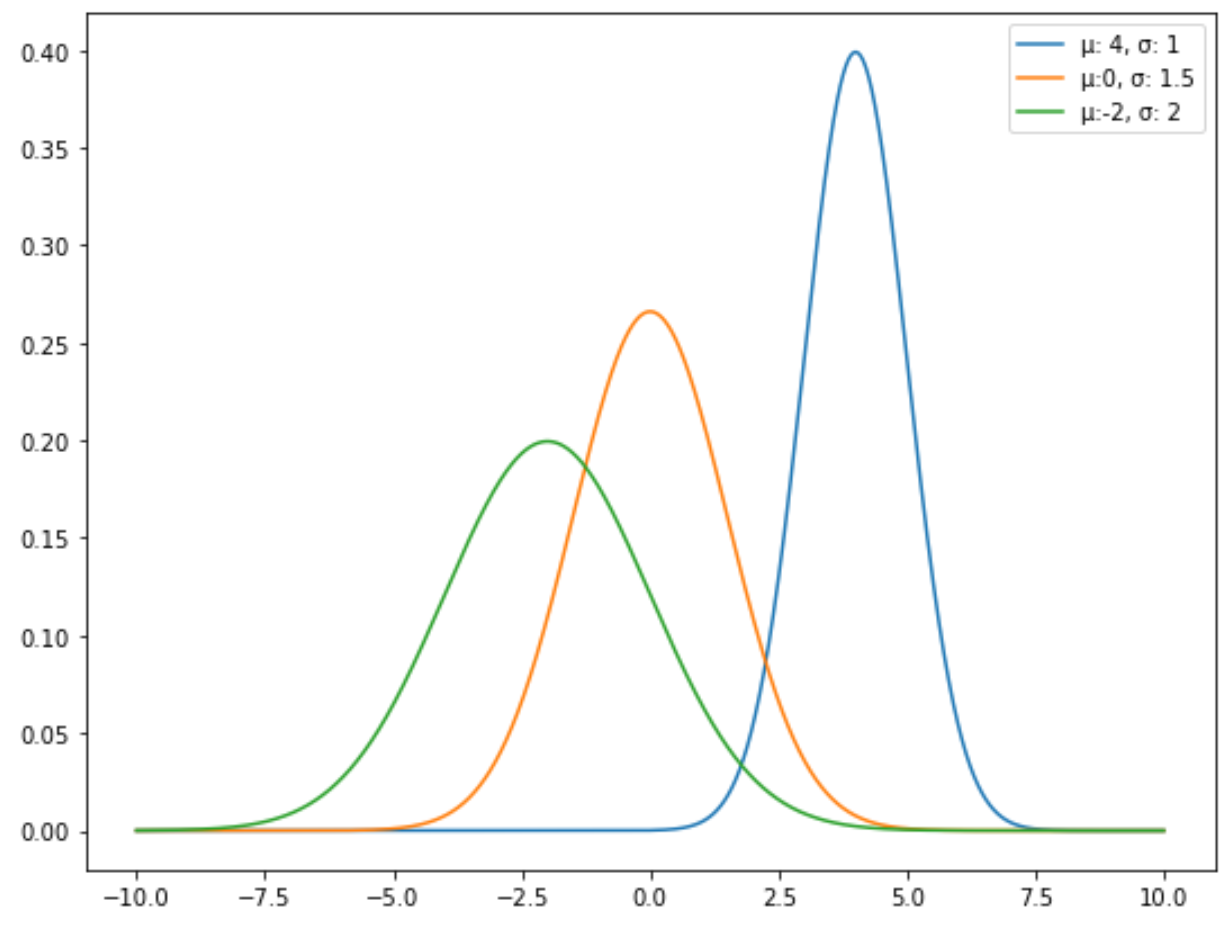
Standart normal dağılım, ortalamanın 0 ve standart sapmanın 1 olduğu özel bir normal dağılım türüdür.

Aşağıdaki grafik standart normal dağılımı göstermektedir:

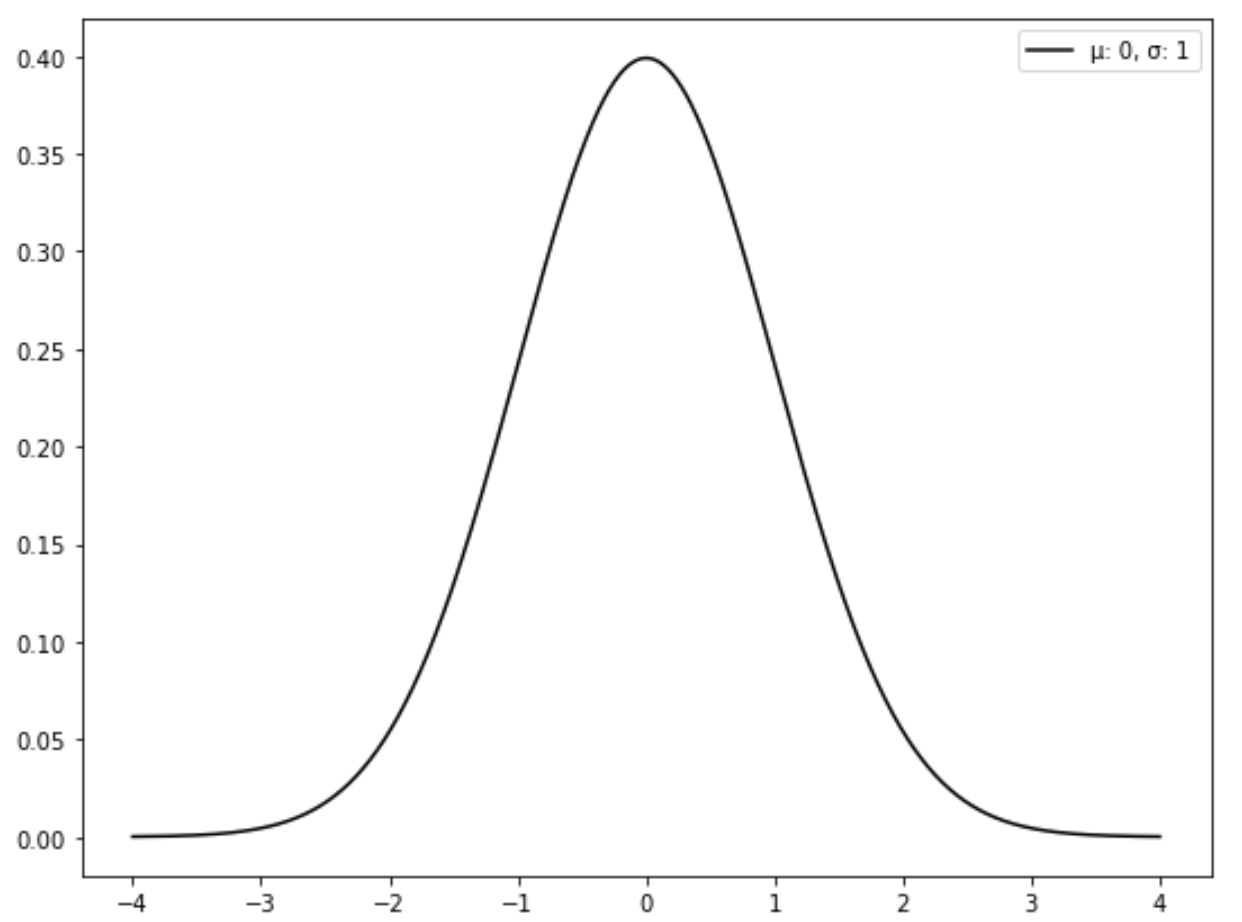
Normal dağılım standart normal dağılıma nasıl dönüştürülür?

Herhangi bir normal dağılım, aşağıdaki formül kullanılarak veri değerleri z-puanlarına dönüştürülerek standart normal dağılıma dönüştürülebilir:

z = (x – μ) / σ

Altın:

• x: bireysel verilerin değeri
• μ: Dağılımın ortalaması
• σ: Dağılımın standart sapması

Örneğin, ortalaması 6 ve standart sapması 2,152 olan aşağıdaki veri setine sahip olduğumuzu varsayalım:

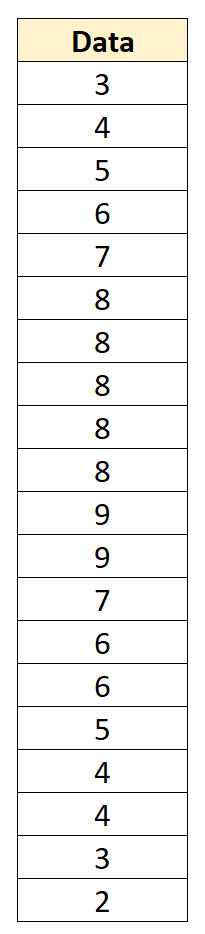
Her bir veri değerini, her değerden 6 çıkarıp 2,152’ye bölerek z puanına dönüştürebiliriz:

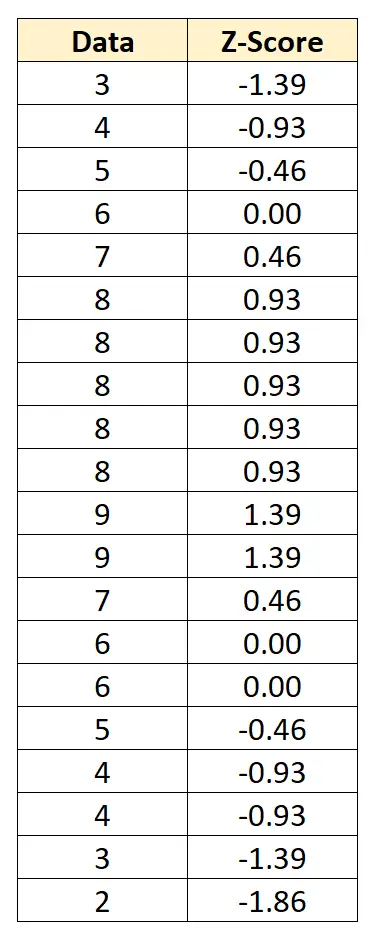
Z-puanı bize her veri noktasının ortalamadan kaç standart sapma olduğunu söyler. Örneğin ilk veri değeri “3” ortalamanın 1,39 standart sapma altındadır.

Bu puan dağılımının ortalamasının ortalaması sıfır, standart sapması ise birdir.

Standart normal dağılım nasıl kullanılır?

Standart bir normal dağılım aşağıdaki özelliklere sahiptir:

• Verilerin yaklaşık %68’i ortalamanın bir standart sapması dahilindedir
• Verilerin yaklaşık %95’i ortalamanın iki standart sapması dahilindedir.
• Verilerin yaklaşık %99,7’si ortalamanın üç standart sapması dahilindedir.

Bu, genel kural olarak bilinir ve bir veri kümesindeki değerlerin dağılımını anlamak için kullanılır.

Örneğin, belirli bir bahçedeki bitkilerin yüksekliğinin ortalama 47,4 inç ve standart sapmanın 2,4 inç olacak şekilde normal dağıldığını varsayalım.

Temel kurala göre bitkilerin yüzde kaçı 54,6 inçten kısadır?

Temel kural, normal dağılıma sahip belirli bir veri seti için veri değerlerinin %99,7’sinin ortalamanın üç standart sapması dahilinde olduğunu belirtir. Bu, değerlerin %49,85’inin ortalama ile ortalamanın üzerindeki üç standart sapma arasında olduğu anlamına gelir.

Bu örnekte 54,6, ortalamanın üç standart sapma üzerindedir. Normal dağılımda veri değerlerinin %50’sinin ortalamadan küçük olduğunu bildiğimiz için %50 + %49,85 = %99,85 değerlerinin toplamı 54,6’dan küçüktür.

Yani bitkilerin %99,85’inin boyu 54,6 inçten kısadır.

Ek kaynaklar

Temel kuralları uygulamada sorunlar
Başparmak Hesaplayıcı Kuralları
Excel’de temel kural nasıl uygulanır?