R vs r-square: fark nedir?

Öğrencilerin istatistikte sıklıkla karıştırdığı iki terim R ve R-kare olup genellikle ^R2 olarak yazılır.

Basit bir doğrusal regresyon bağlamında:

• A: Yordayıcı değişken x ile yanıt değişkeni y arasındaki korelasyon.
• R ² : Regresyon modelinde yordayıcı değişken tarafından açıklanabilen yanıt değişkenindeki varyansın oranı.

Ve çoklu doğrusal regresyon bağlamında:

• A: Yanıt değişkeninin gözlemlenen değerleri ile yanıt değişkeninin tahmin edilen değerleri arasındaki model tarafından yapılan korelasyon.
• R ² : Regresyon modelinin yordayıcı değişkenleri tarafından açıklanabilen yanıt değişkeninin varyansının oranı.

^R2 değerinin 0 ile 1 arasında olduğuna dikkat edin. Değer 1’e ne kadar yakınsa, yordayıcı değişken(ler) ile yanıt değişkeni arasındaki ilişki o kadar güçlü olur.

Aşağıdaki örnekler, basit doğrusal regresyon ve çoklu doğrusal regresyon modellerinde R ve R-kare değerlerinin nasıl yorumlanacağını göstermektedir.

Örnek 1: Basit doğrusal regresyon

Belirli bir matematik dersinde 12 öğrencinin çalışma saatlerini ve kazandığı sınav puanlarını gösteren aşağıdaki veri setine sahip olduğumuzu varsayalım:

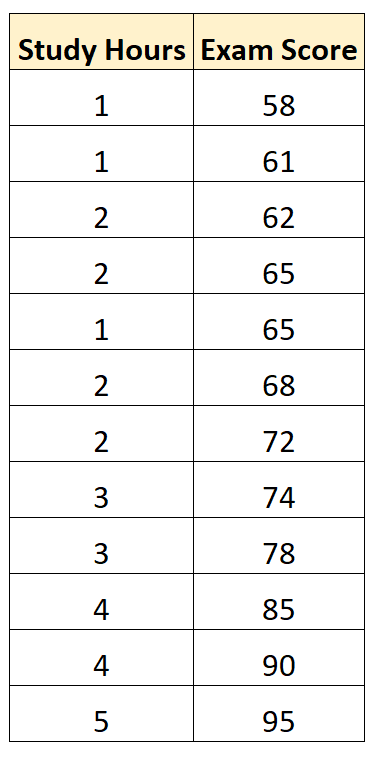
İstatistiksel yazılımlar (Excel, R, Python, SPSS vb. gibi) kullanarak, tahmin değişkeni olarak “çalışma saatlerini” ve yanıt değişkeni olarak “sınav notunu” kullanarak basit bir doğrusal regresyon modeli uydurabiliriz.

Bu model için aşağıdaki çıktıyı bulabiliriz:

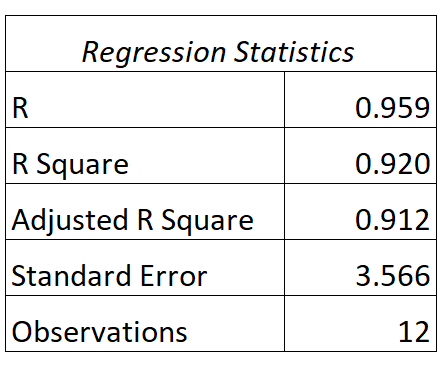
Bu modelin R ve R kare değerlerini şu şekilde yorumlayabilirsiniz:

• C: Çalışılan saat ile sınav puanı arasındaki korelasyon 0,959’dur .
• R ² : Bu regresyon modelinin R karesi 0,920’dir . Bu bize sınav puanlarındaki değişimin %92,0’inin çalışılan saat sayısıyla açıklanabileceğini göstermektedir.

Ayrıca ^R2 değerinin basitçe R değerinin karesine eşit olduğuna dikkat edin:

^R2 = R * R = 0,959 * 0,959 = 0,920

Örnek 2: Çoklu doğrusal regresyon

Belirli bir matematik dersinde 12 öğrencinin çalışılan saatleri, mevcut öğrenci notunu ve kazandığı sınav notunu gösteren aşağıdaki veri setine sahip olduğumuzu varsayalım:

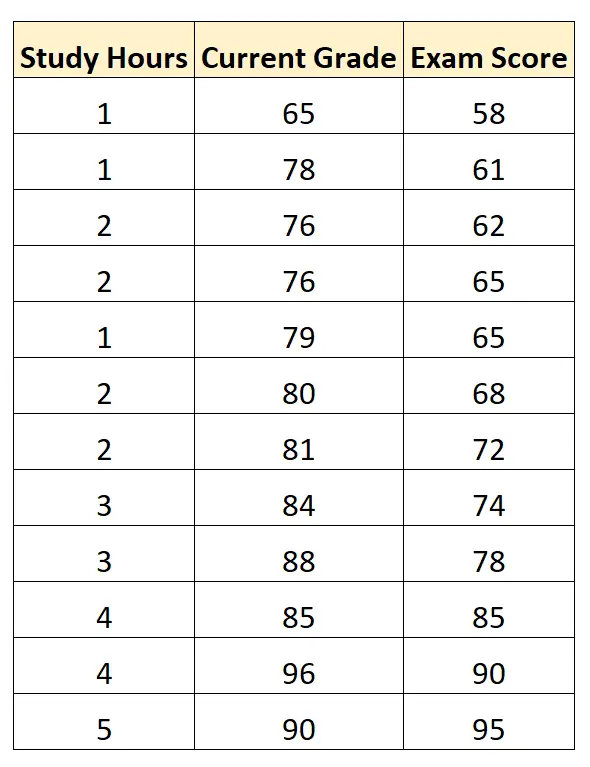
İstatistiksel yazılım kullanarak, “çalışma saatleri” ve “şu anki not”u yordayıcı değişkenler olarak ve “sınav notu”nu yanıt değişkeni olarak kullanarak çoklu doğrusal regresyon modelini yerleştirebiliriz.

Bu model için aşağıdaki çıktıyı bulabiliriz:

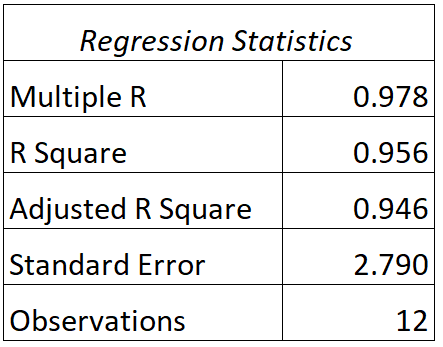
Bu modelin R ve R kare değerlerini şu şekilde yorumlayabilirsiniz:

• C: Gerçek test puanları ile modelin tahmin edilen test puanları arasındaki korelasyon 0,978’dir .
• R ² : Bu regresyon modelinin R karesi 0,956’dır . Bu bize, sınav puanlarındaki farklılığın %95,6’sının çalışılan saat sayısı ve öğrencinin sınıftaki mevcut notu ile açıklanabileceğini göstermektedir.

Ayrıca ^R2 değerinin basitçe R değerinin karesine eşit olduğuna dikkat edin:

^R2 = R * R = 0,978 * 0,978 = 0,956

Ek kaynaklar

İyi bir R-kare değeri nedir?
Karelerin Toplamına İlişkin Nazik Bir Kılavuz: SST, SSR, SSE