Frekans (istatistik)

Bu makale istatistikte frekans kavramının ne olduğunu açıklamaktadır. Böylece istatistiklerde frekansın tanımını, mevcut farklı frekans türlerini ve son olarak bir frekans tablosunun nasıl oluşturulacağını bulacaksınız.

İstatistiklerde frekans nedir?

İstatistiklerde sıklık , bir değerin bir veri kümesinde görünme sayısıdır. Basitçe söylemek gerekirse frekans, bir değerin istatistiksel bir örnekte tekrarlanma sayısıdır.

Örneğin bir ankette beş kişi en sevdikleri rengin mavi olduğunu söylerse mavi rengin sıklığı 5’e eşit olur.

Genel olarak istatistikte, i indeksli f harfi, i değerinin frekansını temsil etmek için kullanılır, dolayısıyla frekansın sembolü _fi’dir .

Tüm frekansların toplamı örnekteki toplam veri sayısını verir. Bu nedenle aşağıdaki formül herhangi bir istatistiksel çalışma için her zaman geçerlidir:

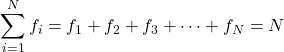
Altın

değerin frekansıdır

Ve

toplam gözlem sayısıdır.

İstatistiklerdeki frekans türleri

İstatistiklerde farklı frekans türleri şunlardır:

• Mutlak frekans : Bir değerin istatistiksel bir örnekte görünme sayısına karşılık gelir.
• Kümülatif Mutlak Frekans : Değerin mutlak frekansı artı tüm küçük değerlerin mutlak frekansları toplanarak hesaplanır.
• Göreli frekans : Bu, mutlak frekansın toplam veri sayısına bölünmesiyle elde edilen değerdir.
• Kümülatif Bağıl Frekans : Değerin bağıl frekansı ile tüm alt değerlerin bağıl frekanslarının toplamına eşittir.

Aşağıdaki bölümde her frekans türünün nasıl hesaplandığını görebilirsiniz.

Frekans tablosu

Tipik olarak istatistikte, bir veri örneğinin frekanslarının hesaplamaları bir frekans tablosunda özetlenir. Aşağıda adım adım bir örnek verilmiştir, böylece nasıl yapılacağını görebilirsiniz.

• 30 kişilik bir sınıfta istatistik konusunda alınan notlar aşağıdaki gibidir. Veri kümesinin frekans tablosunu oluşturun.

Tüm sayılar yalnızca tam sayı olabildiği için ayrık bir değişkendir. Bu nedenle verileri aralıklar halinde gruplamak gerekli değildir.

Bu yüzden her farklı değerin bir satır olacağı bir tablo oluşturmamız gerekiyor. Ek olarak, her bir değerin mutlak frekansını bulmamız gerekir; bunu yapmak için, değerin veri örneğinde kaç kez göründüğünü saymanız yeterlidir.

Tüm mutlak frekansların toplamının toplam veri sayısına eşit olduğunu unutmayın. Bu kurala uyulmaması, belirli bilgileri sağlamayı unuttuğunuz anlamına gelir.

Artık mutlak frekansı bildiğimize göre kümülatif mutlak frekansı bulmamız gerekiyor. Bu hesaplama için iki seçeneğimiz var: ya değerin mutlak frekansı artı en küçük değerlerin tüm mutlak frekanslarını toplarız ya da tam tersine, değerin mutlak frekansı artı önceki değerin kümülatif mutlak frekansını ekleriz.

Son değerin kümülatif mutlak frekansı her zaman toplam veri sayısına karşılık gelir; hesaplamaların doğru olduğunu doğrulamak için bu numarayı kullanabilirsiniz.

Daha sonra, mutlak frekansın toplam veri noktası sayısına (30) bölünmesiyle hesaplanan göreceli frekansı belirlememiz gerekir:

Tüm bağıl frekansların toplamının her zaman 1’e eşit olduğunu unutmayın, aksi halde frekans tablosundaki bazı hesaplamalar yanlış demektir.

Son olarak, birikmiş bağıl frekansın çıkarılması yeterlidir. Bunu yapmak için, söz konusu değerin göreceli frekansını artı önceki tüm göreceli frekansları veya aynı anlama gelen önceki birikmiş göreceli frekansı eklemelisiniz:

Kısaca sorunlu verinin tüm frekanslarını içeren frekans tablosu şu şekildedir: