Mükemmel çoklu bağlantı nedir? (tanım ve örnekler)

İstatistiklerde, çoklu doğrusallık, iki veya daha fazla yordayıcı değişkenin regresyon modelinde benzersiz veya bağımsız bilgi sağlamayacak şekilde birbiriyle yüksek düzeyde korelasyona sahip olması durumunda ortaya çıkar.

Değişkenler arasındaki korelasyon derecesi yeterince yüksekse, bu durum regresyon modelinin yerleştirilmesinde ve yorumlanmasında sorunlara neden olabilir.

Çoklu doğrusallığın en uç durumu, mükemmel çoklu doğrusallık olarak adlandırılır. Bu, iki veya daha fazla öngörücü değişkenin birbiriyle tam bir doğrusal ilişkiye sahip olması durumunda ortaya çıkar.

Örneğin aşağıdaki veri setine sahip olduğumuzu varsayalım:

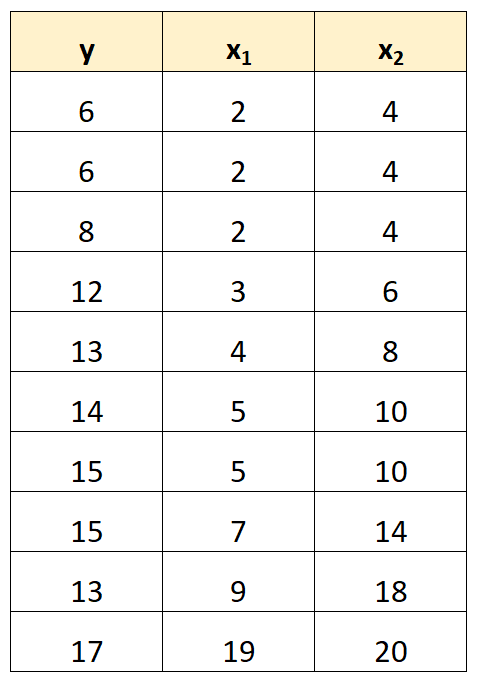
Tahmin değişkeni x _2’nin değerlerinin basitçe x _1’in 2 ile çarpılan değerleri olduğuna dikkat edin.

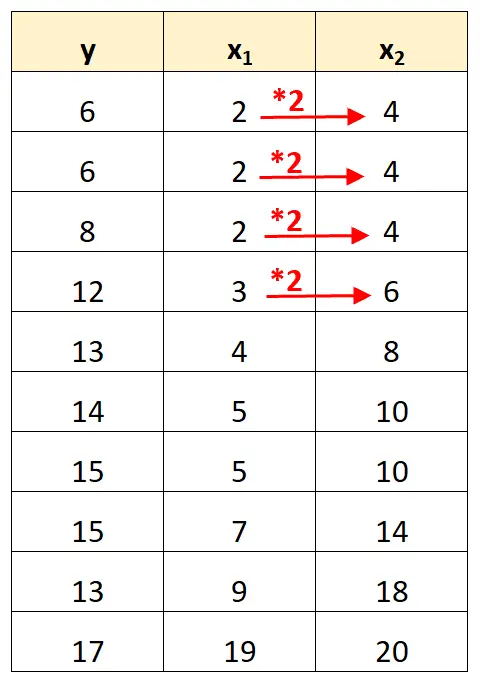
Bu mükemmel çoklu bağlantının bir örneğidir.

Mükemmel çoklu bağlantı sorunu

Bir veri setinde mükemmel çoklu bağlantı mevcut olduğunda, sıradan en küçük kareler, regresyon katsayılarının tahminlerini üretemez.

Aslında, başka bir yordayıcı değişkeni ( _x2 ) sabit tutarken, bir yordayıcı değişkenin ( _x1 ) tepki değişkeni (y) üzerindeki marjinal etkisini tahmin etmek mümkün değildir çünkü _x2 her zaman tam olarak _x1 hareket ettiğinde hareket eder.

Kısacası, mükemmel çoklu doğrusallık, bir regresyon modelinde her katsayı için bir değer tahmin etmeyi imkansız hale getirir.

Mükemmel çoklu bağlantıyla nasıl başa çıkılır?

Mükemmel çoklu doğrusallığı ele almanın en basit yolu, başka bir değişkenle tam doğrusal ilişkiye sahip olan değişkenlerden birini çıkarmaktır.

Örneğin, önceki veri kümemizde tahmin değişkeni olarak x _2’yi basitçe kaldırabilirdik.

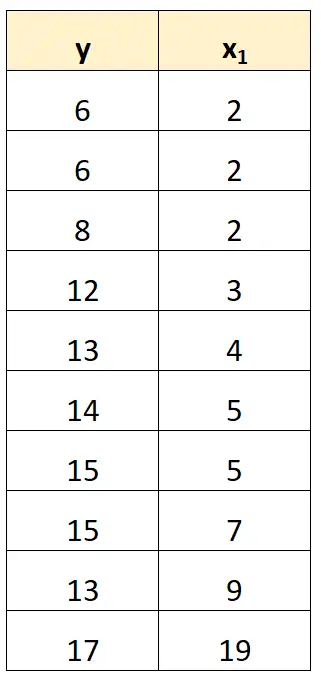
Daha sonra _x1’i yordayıcı değişken olarak ve y’yi yanıt değişkeni olarak kullanarak bir regresyon modeli yerleştirirdik.

Mükemmel çoklu bağlantı örnekleri

Aşağıdaki örnekler uygulamada mükemmel çoklu bağlantının en yaygın üç senaryosunu göstermektedir.

1. Bir yordayıcı değişken diğerinin katıdır

Belirli bir yunus türünün ağırlığını tahmin etmek için “santimetre cinsinden yükseklik” ve “metre cinsinden yükseklik” kullanmak istediğimizi varsayalım.

Veri setimiz şöyle görünebilir:

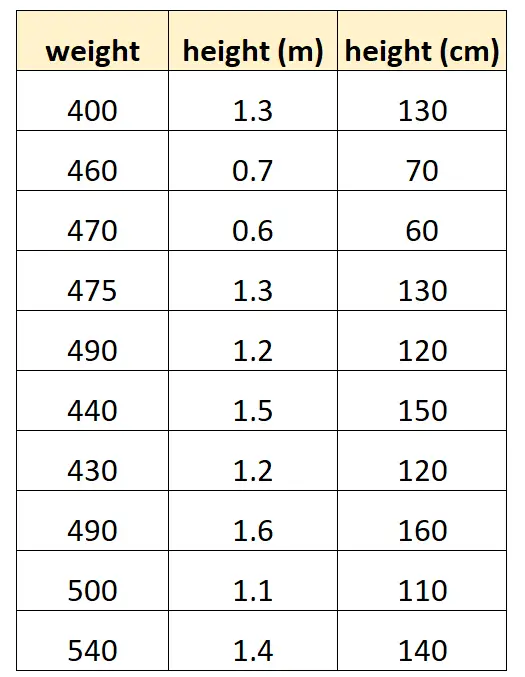
“Santimetre cinsinden yükseklik” değerinin “metre cinsinden yükseklik”in 100 ile çarpımına eşit olduğuna dikkat edin. Bu, mükemmel bir çoklu bağlantı durumudur.

Bu veri kümesini kullanarak R’ye çoklu doğrusal regresyon modeli uydurmaya çalışırsak, “metre” tahmin değişkeni için bir katsayı tahmini üretemeyeceğiz:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. Bir yordayıcı değişken, başka bir değişkenin dönüştürülmüş versiyonudur

Basketbol oyuncularının reytingini tahmin etmek için “puan” ve “ölçeklendirilmiş puan” kullanmak istediğimizi varsayalım.

“Ölçeklendirilmiş noktalar” değişkeninin şu şekilde hesaplandığını varsayalım:

Ölçeklendirilmiş noktalar = (noktalar – μ _noktalar ) / σ _noktalar

Veri setimiz şöyle görünebilir:

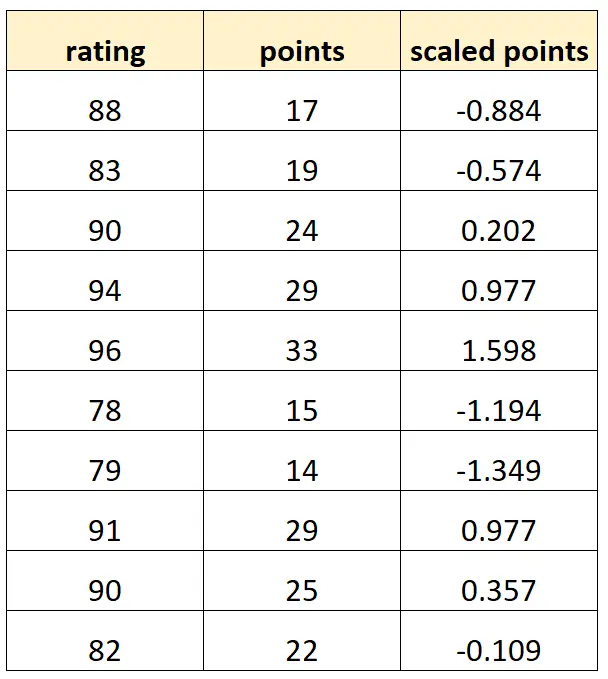
Her “ölçeklendirilmiş puan” değerinin yalnızca “puanların” standartlaştırılmış bir versiyonu olduğunu unutmayın. Bu mükemmel bir çoklu bağlantı durumudur.

Bu veri kümesini kullanarak R’ye çoklu doğrusal regresyon modeli uydurmaya çalışırsak, “ölçeklendirilmiş noktalar” yordayıcı değişkeni için bir katsayı tahmini üretemeyeceğiz:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. Kukla değişken tuzağı

Mükemmel çoklu doğrusallığın meydana gelebileceği başka bir senaryo , kukla değişken tuzağı olarak bilinir. Bu, bir regresyon modelinde kategorik bir değişkeni alıp onu 0, 1, 2 vb. değerlerini alan bir “kukla değişkene” dönüştürmek istediğimiz zamandır.

Örneğin, geliri tahmin etmek için “yaş” ve “medeni durum” yordayıcı değişkenlerini kullanmak istediğimizi varsayalım:

“Medeni durum”u yordayıcı değişken olarak kullanmak için öncelikle onu kukla değişkene dönüştürmeliyiz.

Bunu yapmak için “Bekar”ı temel değer olarak bırakabiliriz, çünkü bu en sık gerçekleşir ve “Evli” ve “Boşanmış”a 0 veya 1 değerlerini aşağıdaki gibi atayabiliriz:

Aşağıdaki gibi üç yeni kukla değişken yaratmak bir hata olacaktır:

Bu durumda “Bekar” değişkeni, “Evli” ve “Boşanmış” değişkenlerinin mükemmel bir doğrusal birleşimidir. Bu mükemmel çoklu bağlantının bir örneğidir.

Bu veri kümesini kullanarak R’ye çoklu doğrusal regresyon modeli uydurmaya çalışırsak, her yordayıcı değişken için bir katsayı tahmini üretemeyeceğiz:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

Ek kaynaklar

Regresyonda Çoklu Bağlantı ve VIF Kılavuzu
R’de VIF nasıl hesaplanır
Python’da VIF nasıl hesaplanır
Excel’de VIF nasıl hesaplanır