Ki-kare dağılımı
Bu makalede ki-kare dağılımının ne olduğu ve ne için kullanıldığı açıklanmaktadır. Ayrıca ki-kare dağılım grafiğini ve özelliklerini bulacaksınız.
Ki-kare dağılımı nedir?
Ki-kare dağılımı sembolü χ² olan bir olasılık dağılımıdır. Daha kesin olarak Ki-kare dağılımı, normal dağılıma sahip k bağımsız rastgele değişkenin karelerinin toplamıdır.
Dolayısıyla Ki-kare dağılımı k serbestlik derecesine sahiptir. Bu nedenle, bir Ki-kare dağılımı, temsil ettiği normal dağılımlı değişkenlerin karelerinin toplamı kadar serbestlik derecesine sahiptir.
![Rendered by QuickLaTeX.com \displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-9ea0bf7a87071883ceae5e419bae9e71_l3.png)
Ki-kare dağılımı Pearson dağılımı olarak da bilinir.
Ki-kare dağılımının gama dağılımının özel bir durumu olduğu unutulmamalıdır.
Ki-kare dağılımı istatistiksel çıkarımlarda, örneğin hipotez testlerinde ve güven aralıklarında yaygın olarak kullanılır. Aşağıda bu tür olasılık dağılımının uygulamalarının neler olduğunu göreceğiz.
Ki-kare dağılım grafiği
Ki-kare dağılımının tanımını gördükten sonra, bu tür dağılımın grafiksel olarak temsil edilen birkaç örneğini göreceğiz. Aşağıda ki-kare dağılımının olasılık grafiğinin serbestlik derecesine bağlı olarak nasıl değiştiğini görebilirsiniz.
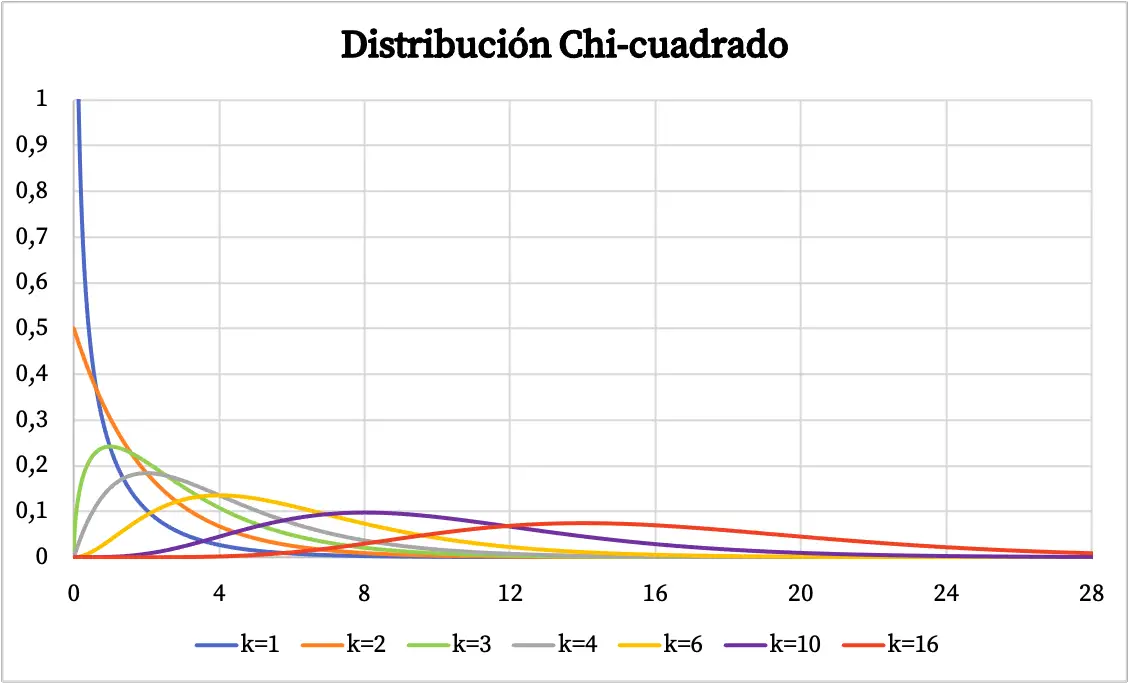
Ki-kare dağılımının yoğunluk fonksiyonu yukarıdaki grafikte gösterilmiştir. Öte yandan ki-kare kümülatif olasılık dağılım fonksiyonunun grafiği şu şekildedir:
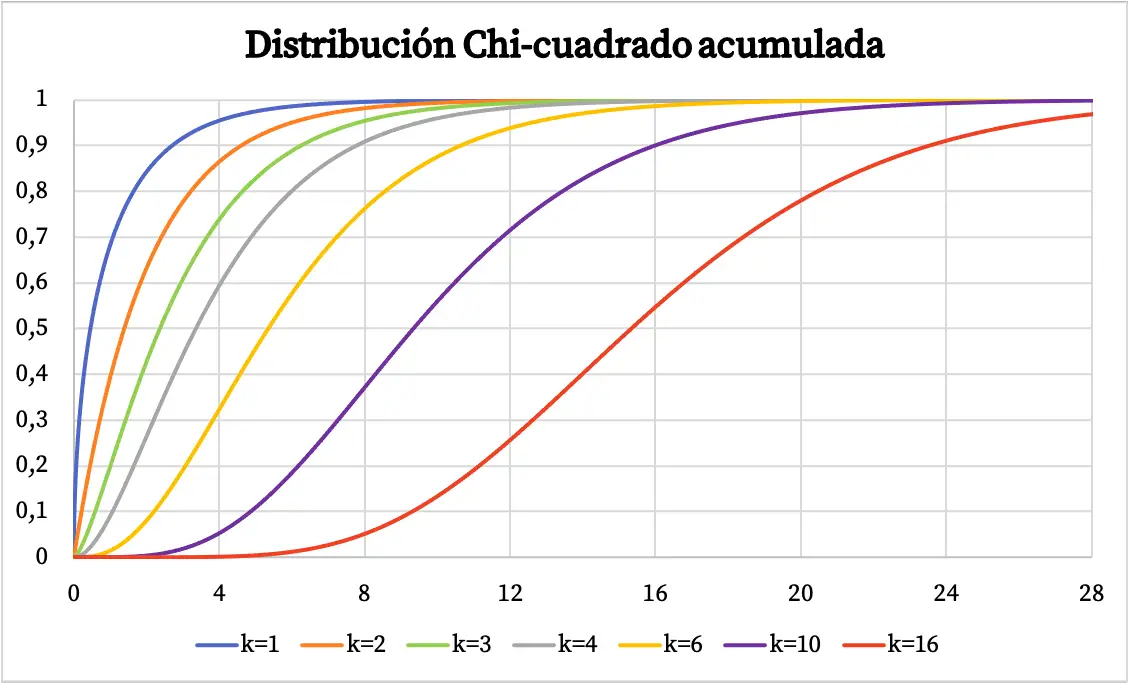
Ki-kare dağılımının özellikleri
Bu bölümde Ki-kare dağılımının olasılık teorisi ve istatistiğe ilişkin en önemli özelliklerini göreceğiz.
- Ki-kare dağılımının ortalaması serbestlik derecesine eşittir.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-8a7926aa60ec788064c47a5a34e641ab_l3.png)
- Ki-kare dağılımının varyansı, dağılımın serbestlik derecesinin iki katına eşittir.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cffd659f19d8ed8260fcaf53dc6dd83f_l3.png)
- Dağıtım birden fazla serbestlik derecesine sahip olduğu sürece, ki-kare dağılımının modu, serbestlik derecesinden iki birim daha azdır.
![]()
- X=0 ise Ki-kare dağılımının yoğunluk fonksiyonu sıfırdır. Bununla birlikte, x’in 0’dan büyük değerleri için Ki-kare dağılımının yoğunluk fonksiyonu aşağıdaki formülle tanımlanır:
![]()
- Ki-kare dağılımının kümülatif dağılım fonksiyonu aşağıdaki formüle göre yönetilir:
![]()
- Ki-kare dağılımının çarpıklık katsayısı, sekiz bölümünün karekökünün dağılımın serbestlik derecesi sayısına bölünmesiyle elde edilir.
![]()
- Ki-kare dağılımının basıklığı aşağıdaki ifade kullanılarak hesaplanır:
![]()
- Merkezi limit teoremine bağlı olarak, eğer k yeterince büyükse, ki-kare dağılımına normal bir dağılımla yaklaşılabilir.
![]()
Ki-kare dağılımının uygulamaları
Ki-kare dağılımının istatistikte birçok farklı uygulaması vardır. Aslında değişkenler arasındaki bağımsızlığı ve teorik dağılıma uyumun iyiliğini kontrol etmek için kullanılan ki-kare testi bile vardır. Örneğin, bir numunenin verilerinin Poisson dağılımına uygun olup olmadığını belirlemek için Ki-kare testi kullanılabilir.
Doğrusal regresyon analizinde ki-kare dağılımı, normal dağılım gösteren bir popülasyonun ortalamasını tahmin etmek ve doğrusal regresyon çalışma çizgisinin eğimini tahmin etmek için de kullanılır.
Son olarak Ki kare dağılımı, Snedecor F dağılımı ile olan ilişkisi nedeniyle varyans analizine de katılmaktadır.