R'de merkezi limit teoremi nasıl uygulanır (örneklerle)

Merkezi limit teoremi, popülasyon dağılımı normal olmasa bile, örneklem büyüklüğü yeterince büyükse, bir örneklem ortalamasının örnekleme dağılımının yaklaşık olarak normal olduğunu belirtir.

Merkezi limit teoremi ayrıca örnekleme dağılımının aşağıdaki özelliklere sahip olacağını belirtir:

1. Örnekleme dağılımının ortalaması nüfus dağılımının ortalamasına eşit olacaktır:

x = µ

2. Örnekleme dağılımının standart sapması, nüfus dağılımının standart sapmasının örneklem büyüklüğüne bölünmesine eşit olacaktır:

s = σ /n

Aşağıdaki örnek, merkezi limit teoreminin R’de nasıl uygulanacağını gösterir.

Örnek: Merkezi limit teoreminin R’de uygulanması

Bir kaplumbağanın kabuğunun genişliğinin minimum 2 inç ve maksimum 6 inç genişlikte düzgün bir dağılım izlediğini varsayalım.

Yani rastgele bir kaplumbağa seçip kabuğunun genişliğini ölçersek, genişliğinin de muhtemelen 2 ile 6 inç arasında olması muhtemeldir.

Aşağıdaki kod, R’de 2 ila 6 inç arasında eşit olarak dağıtılmış 1.000 kaplumbağanın kabuk genişliklerinin ölçümlerini içeren bir veri kümesinin nasıl oluşturulacağını gösterir:

 #make this example reproducible
set. seeds (0)

#create random variable with sample size of 1000 that is uniformly distributed
data <- runif(n=1000, min=2, max=6)

#create histogram to visualize distribution of turtle shell widths
hist(data, col=' steelblue ', main=' Histogram of Turtle Shell Widths ')

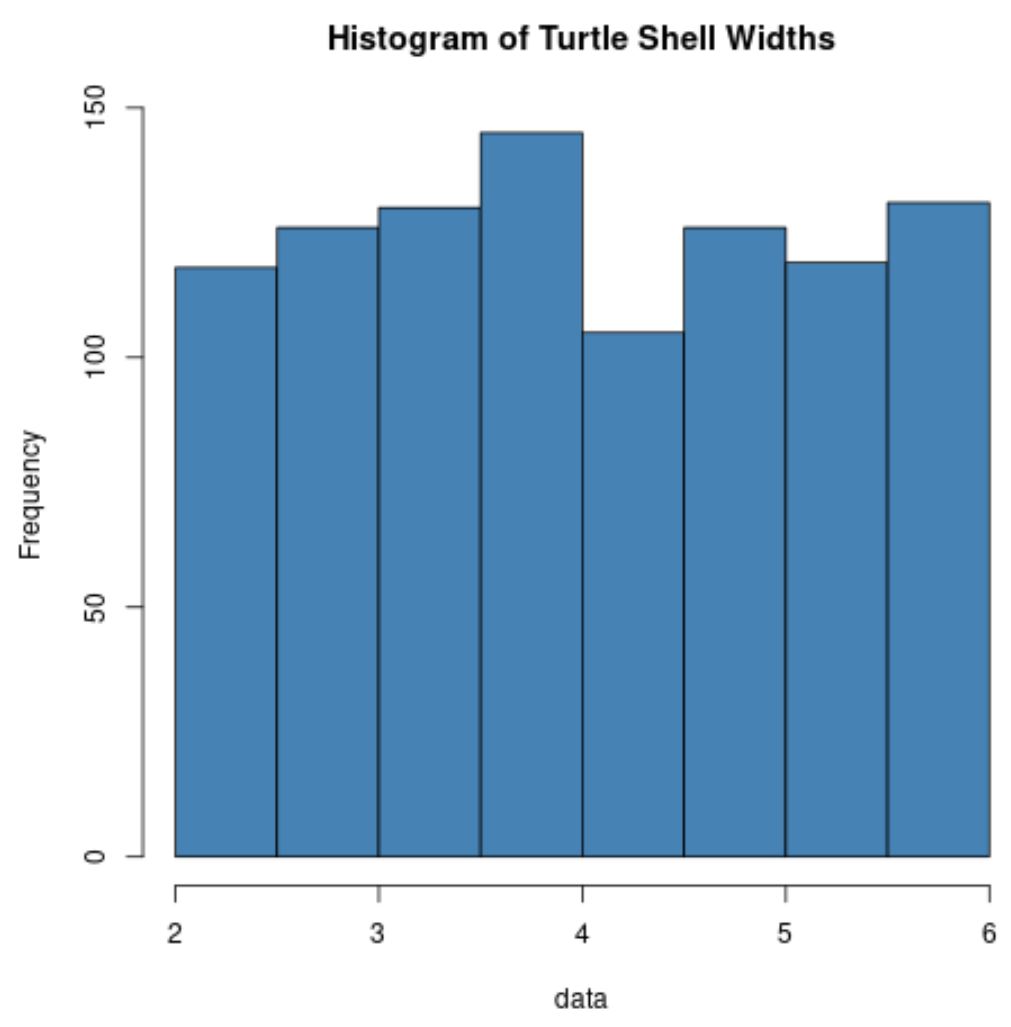
Kaplumbağa kabuğu genişliklerinin dağılımının normalde hiç dağılmadığını unutmayın.

Şimdi bu popülasyondan 5 kaplumbağanın tekrarlanan rastgele örneklerini aldığımızı ve örnek ortalamasını tekrar tekrar ölçtüğümüzü hayal edin.

Aşağıdaki kod, bu işlemin R’de nasıl yapılacağını ve örnek ortalamaların dağılımını görselleştirmek için bir histogramın nasıl oluşturulacağını gösterir:

 #create empty vector to hold sample means
sample5 <- c()

#take 1,000 random samples of size n=5
n = 1000
for (i in 1:n){
sample5[i] = mean(sample(data, 5, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample5)

[1] 4.008103

sd(sample5)

[1] 0.5171083 

#create histogram to visualize sampling distribution of sample means
hist(sample5, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 5 ') 

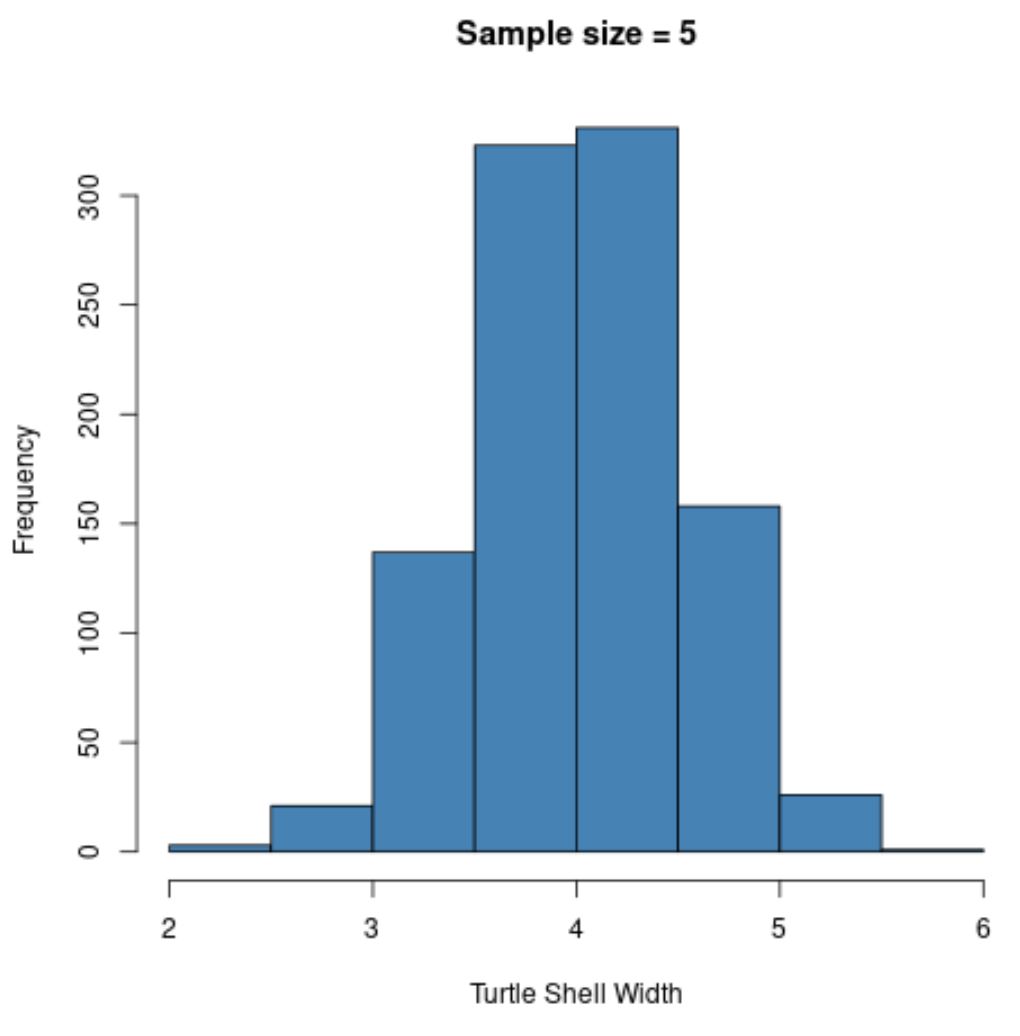
Örneklerin geldiği dağılım normal dağılmamış olmasına rağmen, örnek ortalamalarının örnekleme dağılımının normal dağılmış göründüğüne dikkat edin.

Ayrıca bu örnekleme dağılımı için örnek ortalamasını ve örnek standart sapmasını da not edin:

• x̄ : 4,008
• s : 0,517

Şimdi kullandığımız örnek boyutunu n=5’ten n=30’a çıkardığımızı ve örnek ortalamalarının histogramını yeniden oluşturduğumuzu varsayalım:

 #create empty vector to hold sample means
sample30 <- c()

#take 1,000 random samples of size n=30
n = 1000
for (i in 1:n){
sample30[i] = mean(sample(data, 30, replace= TRUE ))
}

#calculate mean and standard deviation of sample means
mean(sample30)

[1] 4.000472

sd(sample30)

[1] 0.2003791

#create histogram to visualize sampling distribution of sample means
hist(sample30, col = ' steelblue ', xlab=' Turtle Shell Width ', main=' Sample size = 30 ') 

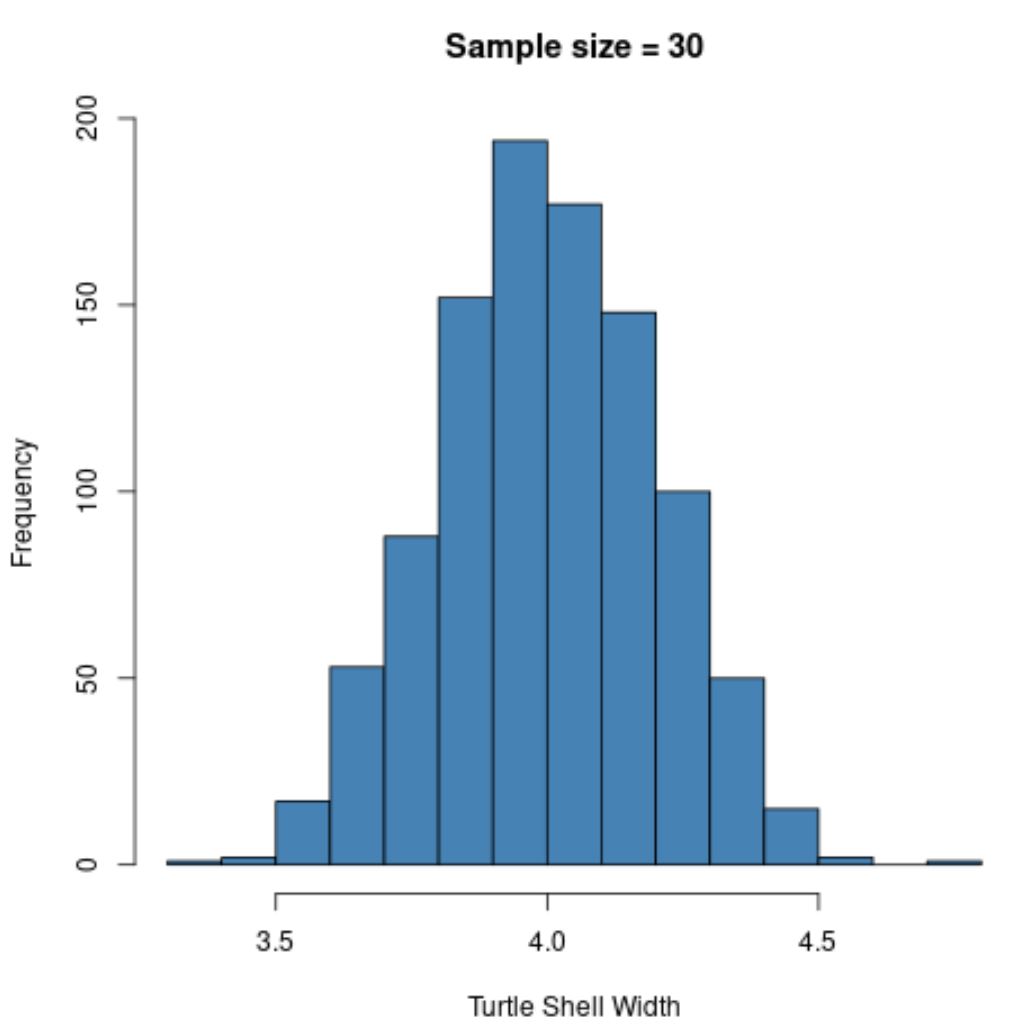
Örnekleme dağılımı yine normal olarak dağıtılır , ancak örnek standart sapması daha da küçüktür:

• : 0,200

Bunun nedeni, önceki örneğe (n=5) kıyasla daha büyük bir örneklem boyutu (n=30) kullanmamızdır, dolayısıyla örnek ortalamalarının standart sapması daha da küçüktür.

Eğer giderek daha büyük örnekler kullanmaya devam edersek, örnek standart sapmasının giderek küçüldüğünü göreceğiz.

Bu, pratikte merkezi limit teoremini göstermektedir.

Ek kaynaklar

Aşağıdaki kaynaklar merkezi limit teoremi hakkında ek bilgi sağlar:

Merkezi Limit Teoremine Giriş
Merkezi Limit Teoremi Hesaplayıcı
Merkezi Limit Teoremini Gerçek Hayatta Kullanmaya İlişkin 5 Örnek