Örnek ortalama

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu yazıda istatistiklerde örnek ortalamasının ne olduğunu öğreneceksiniz. Benzer şekilde, bir numunenin ortalamasını nasıl hesaplayacağınızı, çözülmüş bir alıştırmayı ve ayrıca herhangi bir numunenin ortalamasını hesaplamak için çevrimiçi bir hesap makinesini bulacaksınız.

Örnek ne anlama geliyor?

İstatistikte örnek ortalaması , bir örnekteki değerlerin ortalamasıdır. Örnek ortalamasını hesaplamak için örnekteki tüm değerlerin toplanması ve ardından örnekteki toplam veri sayısına bölünmesi gerekir.

Örnek ortalamanın sembolü

$\overline{x}$

İstatistiksel bir çalışmada, genellikle bir popülasyonun tüm değerleri bilinmez; bu nedenle, onu analiz etmek ve elde edilen sonuçları tüm popülasyona tahmin etmek için popülasyonun bir örneği seçilir. Bu nedenle, örneklem ortalaması popülasyon ortalamasını tahmin etmek için kullanılır.

Ortalama Formül Örneği

Örnek ortalaması, tüm örnek değerlerinin toplamının örnek büyüklüğüne bölünmesine eşittir. Yani örnek ortalamasını hesaplamak için örnekteki tüm değerler toplanır ve ardından örnekteki toplam veri sayısına bölünür.

Bu nedenle, örnek ortalamasını hesaplama formülü şöyledir:

$\displaystyle\overline{x}=\frac{\displaystyle \sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+\dots +x_n}{n}$

👉Herhangi bir veri setinin örnek ortalamasını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Örnek ortalamasının bir örnekten alınan veriler kullanılarak hesaplandığını, dolayısıyla popülasyon ortalamasının değerinin hesaplanan değerden farklı olabileceğini unutmayın.

Örnek Ortalama Hesaplama Örneği

Artık örnek ortalamanın tanımını ve formülünün ne olduğunu bildiğimize göre, basit bir örnek çözerek bir veri kümesinden örnek ortalamanın nasıl elde edileceğini görelim.

Jose şehir merkezine taşınmak istiyor ama fazla vakti olmadığından kiralık tüm dairelerin fiyatlarını analiz edemiyor. Şehir merkezinde yaşamanın size ne kadara mal olacağını öğrenmek için yalnızca beş dairenin (aşağıda gösterilen) kira fiyatına bakmaya karar veriyorsunuz. Numunenin ortalama fiyatı nedir?

€600 €430 €820 €575 €950

Örnek ortalamayı bulmak için tüm örnek değerleri toplamamız ve ardından toplam gözlem sayısına (5) bölmemiz gerekir. Bu nedenle örnek ortalama formülünü uygularız:

$\displaystyle\overline{x}=\frac{\displaystyle\sum_{i=1}^n x_i}{n}=\frac{x_1+x_2+x_3+x_4+x_5}{n}$

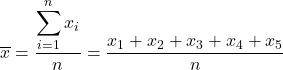
Daha sonra verileri formülde yerine koyarız ve örnek ortalamayı hesaplarız:

$\overline{x}=\cfrac{600+430+820+575+950}{5}=675$

Kısaca örnek için seçilen daire örneklerinin ortalama fiyatı 675€’dur.

Ortalama Hesaplayıcı Örneği

Örnek ortalamasını hesaplamak için herhangi bir istatistiksel örnekteki verileri aşağıdaki hesaplayıcıya girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Örnek ortalaması ve popülasyon ortalaması

Popülasyon ortalaması istatistiksel popülasyonun ortalamasıdır. Dolayısıyla nüfus ortalaması, üzerinde istatistiksel bir çalışmanın yapılması amaçlanan tüm unsurların ortalamasıdır.

Dolayısıyla örnek ortalaması ile popülasyon ortalaması arasındaki fark , örnek ortalamasının örnek değerlerin ortalaması olması, popülasyon ortalamasının ise popülasyondaki değerlerin ortalaması olmasıdır.

Örnek ortalamasını popülasyon ortalamasından ayırt etmek için farklı sembollerle temsil edilirler. Örnek ortalamanın sembolü

$\overline{x}$

, nüfus anlamına gelen sembol ise

$\mu$

$\begin{array}{c}\overline{x} = \text{Media muestral}\\[2ex]\mu =\text{Media poblacional}\end{array}$

Örnek ortalaması, nokta tahmini veya aralık tahmini kullanılarak yapılabilen popülasyon ortalamasının değerini tahmin etmek için kullanılır.

➤ Bakınız: Nüfus ortalaması nedir?

Örnek ortalamalarının örnekleme dağılımı

Son olarak örneklemin örnekleme dağılımının ne anlama geldiğine bakalım, çünkü kafa karıştırıcı olabilecek istatistiksel bir kavram.

Öncelikle örnekleme dağılımının ne olduğunu tanımlayarak başlayalım. Örnekleme dağılımı, istatistiksel bir popülasyondan olası tüm örneklerin dikkate alınmasından kaynaklanan dağılımdır.

Bu nedenle, örnek ortalamasının örnekleme dağılımı , bir popülasyondaki olası her örneğin ortalamasının hesaplanmasından kaynaklanan dağılımdır. Yani, bir popülasyondan olası tüm örnekleri incelersek ve örneklerin her birinin ortalamasını hesaplarsak, hesaplanan değerler kümesi, örnek ortalamasının örnekleme dağılımı olur.

Sonuç olarak, örnek ortalama ve örnekleme dağılımı benzer isimlere sahip olsa da, bunların nasıl ayırt edileceğini bilmek gerekir: örnek ortalaması, bir örnekten hesaplanan istatistiksel bir parametredir; Örnekleme dağılımı ise bir dağılımdır. Bu, bir popülasyondan alınabilecek tüm örneklerin incelenmesinden kaynaklanır.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil