Ortalamanın örnekleme dağılımı

İle Dr.benjamin anderson Ağustos 3, 2023 İstatistik 0 Yorum

Bu makale istatistikte ortalamanın örnekleme dağılımının ne olduğunu açıklamaktadır. Ayrıca ortalama örnekleme dağılım formülünü ve adım adım çözülmüş alıştırmayı da bulacaksınız.

Ortalamanın örnekleme dağılımı nedir?

Ortalamanın örnekleme dağılımı (veya ortalamaların örnekleme dağılımı ), bir popülasyondan olası her örneğin örnekleme ortalamasının hesaplanmasından kaynaklanan dağılımdır. Yani, bir popülasyondaki tüm olası örneklerden elde edilen örnek ortalamaları kümesi, ortalamanın örnekleme dağılımını oluşturur.

Veya başka bir deyişle, bir popülasyondan alınabilecek tüm örnekleri incelersek ve örneklerin her birinin ortalamasını hesaplarsak, hesaplanan değerler kümesi, örnek ortalamasının bir örnekleme dağılımını oluşturur.

İstatistikte ortalamanın örnekleme dağılımı, tek bir örnek analiz edilirken anakütle ortalamasının değerine yaklaşma olasılığını hesaplamak için kullanılır.

Ortalamanın örnekleme dağılımı için formül

Ortalama ile normal bir olasılık dağılımını takip eden bir popülasyon göz önüne alındığında

$\mu$

ve standart sapma

$\sigma$

ve boyut örnekleri çıkarıldı

$n$

ortalamanın örnekleme dağılımı aşağıdaki özelliklere sahip bir normal dağılımla da tanımlanacaktır:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Altın

$\mu_{\overline{x}}$

ortalamanın örnekleme dağılımının ortalamasıdır ve

$\sigma_{\overline{x}}$

onun standart sapmasıdır. Üstelik,

$\cfrac{\sigma}{\sqrt{n}}$

örnekleme dağılımının standart hatasıdır.

Not: Eğer popülasyon normal bir dağılım izlemiyorsa ancak örneklem büyüklüğü büyükse (n>30), ortalamanın örnekleme dağılımı merkezi limit teoremi ile önceki normal dağılıma da yaklaştırılabilir.

Bu nedenle, ortalamanın örnekleme dağılımı normal bir dağılım izlediğinden, örnek ortalamasına ilişkin herhangi bir olasılığı hesaplama formülü şöyledir:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Altın:

$\overline{x}$

örnek anlamına gelir.
$\mu$

Bu nüfus ortalamasıdır.
$s$

nüfus standart sapmasıdır.
$n$

örneklem büyüklüğüdür.
$Z$

standart normal dağılım N(0,1) tarafından tanımlanan bir değişkendir.

Ortalamanın örnekleme dağılımına ilişkin gerçek dünya örneği

Ortalamanın örnekleme dağılımının tanımını ve ilgili formüllerin neler olduğunu gördükten sonra kavramı daha iyi anlamak için bir örnek çözelim.

Üniversite öğrencilerinin ağırlıkları ortalaması 68 kg, standart sapması 9 kg olan normal bir dağılım izlemektedir. Azimli:
1. Rastgele seçilen 25 öğrenciden oluşan ortalamanın 66 kg’dan az olma olasılığı nedir?
2. Her biri 25 öğrenciden oluşan 300 numune alınırsa kaç numunenin ortalaması 66 kg’dan küçük olur?

Öncelikle ilgili istatistiğin değerini hesaplamamız gerekiyor, bunun için yukarıda gördüğümüz formülü uyguluyoruz:

$\displaystyle Z=\frac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}=\frac{66-68}{\displaystyle\frac{9}{\sqrt{25}}}=-1,11$

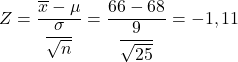
Bu nedenle aradığımız olasılık, Z olasılık tablosundan kolayca elde edilebilecek standart normal dağılımın sol kuyruğunun Z=-1,11 değerine karşılık gelen olasılıktır. Bu nedenle problemin bize sorma olasılığını belirlemek için Z tablosunu kullanırız:

$P[\overline{x}\leq 66]=P[Z\leq -1,11] =0,1335$

➤ Bakınız: Tablo Z

Artık rastgele bir numunenin ortalamasının 66 kg’dan az olma olasılığını bildiğimize göre, 300 eşit numune alarak numune sayısının 66 kg’dan az olduğunu bilmek için hesaplanan olasılığı alınan numunelerin toplam sayısıyla çarpmamız gerekir:

$0,1335\cdot 300 =40,05 \approx 40$

Bu nedenle, çıkarılan örneklerin yaklaşık 40 tanesinin ortalaması 66 kg’ın altında olacaktır.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Ortalamanın örnekleme dağılımı nedir?

Ortalamanın örnekleme dağılımı için formül

Ortalamanın örnekleme dağılımına ilişkin gerçek dünya örneği

yazar hakkında

Dr.benjamin anderson

Yorum ekle