İstatistiklerde mod neden önemlidir?

Mod, bir veri setinde en sık görülen değeri temsil eder.

Bir veri kümesinde hiçbir mod (eğer hiçbir değer tekrarlanmıyorsa), bir mod veya birden fazla mod bulunabilir.

Örneğin aşağıdaki veri kümesindeki mod 19’dur:

Veri kümesi: 3, 4, 11, 15, 19 , 19, 19 , 22 , 22, 23, 23, 26

Bu en sık görülen değerdir.

İstatistiklerde mod aşağıdaki nedenlerden dolayı önemlidir:

Sebep 1 : Bu, bir veri kümesindeki hangi değer(ler)in en yaygın olduğunu bilmemizi sağlar.

Sebep 2 : Ortalama ve medyanın hesaplanamadığı durumlarda kategorik verilerde en sık görülen değeri bulmak açısından faydalıdır.

Sebep 3 : Medyan ve ortalama daha yaygın olarak kullanılsa da (bu makalenin ilerleyen kısımlarında göreceğimiz gibi) bize bir veri kümesinin “merkezinin” nerede olduğuna dair bir fikir verir.

Aşağıdaki örnekler bu nedenlerin her birini pratikte göstermektedir.

Sebep 1: Mod bize hangi değerin en yaygın olduğunu söyler

Diyelim ki Amerika Birleşik Devletleri’ndeki evlerin satış fiyatlarını içeren 100.000 satırlık bir veri kümemiz var:

Bu veri kümesinin modunu hesaplamak için istatistiksel yazılım ( Excel , R , Python vb. gibi) kullandığımızı ve üç mod olduğunu bulduğumuzu varsayalım:

• 280.000$
• 300.000$
• 305.000$

Bu bize hemen veri setindeki en yaygın ev fiyatları hakkında fikir veriyor.

Binlerce modun hesaplanması, veri satırlarına bakmaktan ve hangi ev fiyatlarının en sık meydana geldiğini belirlemeye çalışmaktan çok daha hızlıdır.

Sebep 2: Mod, kategorik verilerdeki en yaygın değeri arar

Belirli bir mahalledeki bireylerin sahip olduğu arabanın rengini bize söyleyen 1000 satırlık bir veri kümemiz olduğunu varsayalım:

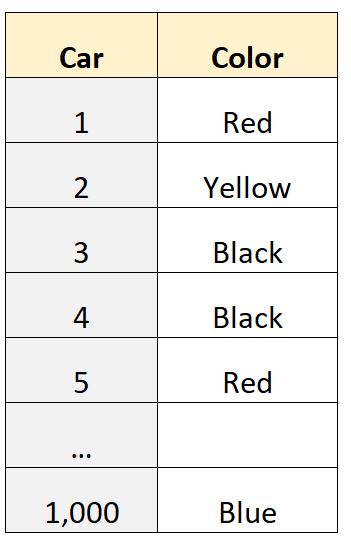
“Renk” değişkeni kategorik bir değişkendir ; bu, değerlerin kategorilere (“kırmızı”, “sarı”, “siyah” vb.) ait olduğu anlamına gelir ve bu nedenle ortalama veya medyan gibi niceliksel bir değer hesaplayamayız. .

Ancak veri setindeki en yaygın değeri temsil ettiği için modu hesaplayabiliriz.

Örneğin, bu veri kümesinin modunun “siyah” olduğunu belirlemek için istatistik yazılımı kullanabiliriz, bu da bize bu veri kümesindeki en yaygın araba renginin siyah olduğunu söyler.

Sebep 3: Mod bize bir veri kümesinin merkezinin nerede olduğuna dair bir fikir verir

Mod aynı zamanda merkezi eğilimin bir ölçüsü olarak da kabul edilir; bu, bize veri kümesinin “merkezinin” nerede olduğuna dair bir fikir verebileceği anlamına gelir.

Örneğin, bir sınıftaki 20 farklı öğrencinin sınav puanlarını gösteren aşağıdaki veri setine sahip olduğumuzu varsayalım:

Modun 82 olduğu ortaya çıkıyor – bu en yaygın sınav puanıdır. Bu aynı zamanda “temel” inceleme puanı değerinin bu veri kümesinde nerede bulunduğunun da iyi bir göstergesi olarak ortaya çıkıyor.

Ancak bunun yerine aşağıdaki sınav sonuçları veri kümesine sahip olduğumuzu varsayalım:

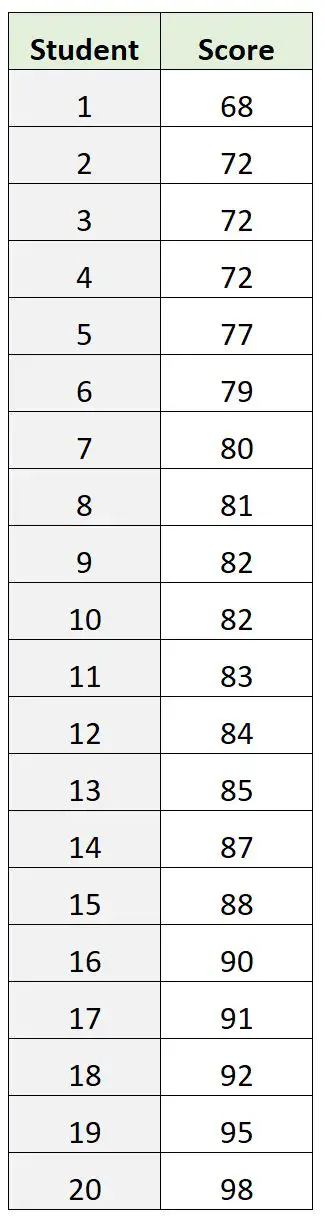
Bu veri setinde 72 moda sınavı puanıdır. Ancak bu, sınavın “temel” puanının nerede olduğuna dair zayıf bir gösterge olarak ortaya çıkıyor.

Ortalama sınav puanı 82,9 ve medyan sınav puanı 82,5 olup her ikisi de bize modayla ilgili “merkezi” değerin nerede olduğu konusunda daha iyi bir fikir veriyor.

Özet

Bu makalede ele alınan ana noktaların kısa bir özetini burada bulabilirsiniz:

• Mod, bir veri setinde en sık görülen değer(ler)i temsil eder.
• Mod, ortalama ve medyanın kullanılamadığı durumlarda kategorik verilerdeki en yaygın değeri bize bildirir.
• Mod bize bir veri kümesinin “merkezinin” nerede olduğuna dair bir fikir verir ancak ortalama veya medyanla karşılaştırıldığında yanıltıcı olabilir.

Ek kaynaklar

Aşağıdaki eğitimler istatistikteki ortalama, medyan ve mod hakkında ek bilgi sağlar:

İstatistiklerde ortalama neden önemlidir?
Medyan istatistikte neden önemlidir?
Somut Örnekler: Ortalama, Medyan ve Modu Kullanma
Ortalama vs Ne Zaman Kullanılır? Medyan: Örneklerle