Ortalamalardaki fark için hipotez testi
Bu makale istatistikte ortalama hipotez testinin ne gibi bir fark yarattığını ve ne için kullanıldığını açıklamaktadır. Benzer şekilde, ortalamalar arasındaki farka ilişkin bir hipotez testinin nasıl yapılacağını ve adım adım çözülmüş bir alıştırmayı keşfedeceksiniz.
Ortalama fark için hipotez testi nedir?
Ortalamalardaki fark için hipotez testi, iki popülasyonun ortalamalarının farklı olduğu hipotezini reddetmek veya kabul etmek için kullanılan istatistiksel bir testtir. Yani, ortalamalar arasındaki fark hipotez testi, iki popülasyonun ortalamalarının aynı mı yoksa farklı mı olduğunu belirlemek için kullanılır.
Hipotez testinde alınan kararların önceden belirlenmiş bir güven düzeyine dayandığını, dolayısıyla bir hipotez testinin sonucunun her zaman doğru olduğunu garanti edemeyeceğini, bunun yerine en olası sonucun doğru olduğunu unutmayın.
İki ortalamanın farkına yönelik hipotez testi, test istatistiğinin hesaplanmasını ve boş hipotezin reddedilip reddedilmeyeceğini kritik değerle karşılaştırmayı içerir. Aşağıda ortalamalar arasındaki fark için bir hipotez testinin nasıl gerçekleştirileceğini göreceğiz.
Son olarak, istatistikte hipotez testine hipotez karşıtlıkları, hipotez testi veya anlamlılık testi de denilebileceğini unutmayın.
Ortalamalardaki Fark için Hipotez Testi Formülü
Ortalamalardaki farka ilişkin hipotezleri test etmek için kullanılması gereken formül, popülasyon varyanslarının bilinip bilinmediğine ve bilinmiyorsa bunların aynı veya farklı olduğunun varsayılıp varsayılamayacağına bağlı olarak değişir. Yani bu bölümde duruma göre hangi formülün kullanılacağını göreceğiz.
Bilinen varyasyonlar
Varyanslar bilindiğinde ortalamalar arasındaki farka ilişkin hipotez testi istatistiğini hesaplama formülü aşağıdaki gibidir:

Altın:
-

standart normal dağılıma uyan, bilinen varyansa sahip iki ortalamanın farkı için hipotez test istatistiğidir.
-

nüfus 1’in ortalamasıdır.
-

nüfus 2’nin ortalamasıdır.
-

örnek 1’in ortalamasıdır.
-

örnek 2’nin ortalamasıdır.
-

popülasyon 1’in standart sapmasıdır.
-

popülasyon 2’nin standart sapmasıdır.
-

örneklem büyüklüğü 1’dir.
-

örneklem büyüklüğü 2’dir.
Bunun en az görülen durum olduğunu unutmayın, dolayısıyla bu formül yalnızca bazı özel durumlarda kullanılır.
Bilinmeyen ve eşit sapmalar
Popülasyon varyanslarının bilinmediği ancak eşit olduğu varsayıldığında ortalamalar arasındaki farka ilişkin hipotez testi istatistiğini hesaplama formülü şöyledir :

Altın:
-

n1 + n2-2 serbestlik derecesine sahip bir Öğrenci t dağılımını takip eden, bilinmeyen varyanslara sahip ortalamalar arasındaki farka yönelik hipotez test istatistiğidir.
-

nüfus 1’in ortalamasıdır.
-

nüfus 2’nin ortalamasıdır.
-

örnek 1’in ortalamasıdır.
-

örnek 2’nin ortalamasıdır.
-

birleşik standart sapmadır.
-

örneklem büyüklüğü 1’dir.
-

örneklem büyüklüğü 2’dir.
İki numunenin birleşik standart sapması aşağıdaki formülle hesaplanır:

Bilinmeyen ve farklı varyasyonlar
Popülasyon varyansları bilinmediğinde ve ayrıca farklı oldukları varsayıldığında, ortalamalar arasındaki farka ilişkin hipotez testi istatistiğini hesaplama formülü aşağıdaki gibidir:

Altın:
-

Öğrenci t dağılımını takip eden, bilinmeyen varyanslara sahip ortalamalar arasındaki farka yönelik hipotez test istatistiğidir.
-

nüfus 1’in ortalamasıdır.
-

nüfus 2’nin ortalamasıdır.
-

örnek 1’in ortalamasıdır.
-

örnek 2’nin ortalamasıdır.
-

popülasyon 1’in standart sapmasıdır.
-

popülasyon 2’nin standart sapmasıdır.
-

örneklem büyüklüğü 1’dir.
-

örneklem büyüklüğü 2’dir.
Ancak bu durumda Öğrenci t dağılımının serbestlik dereceleri aşağıdaki formül kullanılarak hesaplanır:

Ortalamalardaki fark için hipotez testinin somut örneği
Ortalamalar arasındaki farka ilişkin hipotez testi kavramını özümsemeyi bitirmek için, bu tür hipotez testinin somut bir örneğini göreceğiz.
- Rakip iki şirketin maaşları üzerine istatistiksel bir çalışma yapmak istiyorsunuz, daha spesifik olarak iki şirketin ortalama maaşlarının farklı olup olmadığını belirlemek istiyorsunuz. Bunun için bir firmadan 47 işçiden, diğer firmadan ise 55 işçiden numune alınır. Birinci örnekten ortalama 40.000 ABD Doları maaş ve 12.000 ABD Doları standart sapma elde edilirken, ikinci örnekten ortalama 46.000 ABD Doları maaş ve 18.000 ABD Doları standart sapma elde edilmiştir. Ortalama maaşların farklı olup olmadığını belirlemek için %5 anlamlılık düzeyinde bir hipotez testi yapın.
Bu durumda iki ortalamanın farkına ilişkin hipotez testinin sıfır hipotezi ve alternatif hipotezi aşağıdaki gibidir:
![Rendered by QuickLaTeX.com \begin{cases}H_0: \mu_1-\mu_2=0\\[2ex] H_1:\mu_1-\mu_2\neq 0 \end{cases}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4dd9e80c0a87987d689d7b8d99be9d90_l3.png)
Bu durumda nüfus farkları bilinmemekle birlikte rakip şirketler olmaları ve faaliyet gösterdikleri pazarın çalışma koşullarının birbirine çok benzer olması nedeniyle eşit olduğu varsayılabilir. Bu nedenle, ortalamalar arasındaki farka ilişkin hipotez test istatistiği için kullanmamız gereken formül şöyledir:

Bu nedenle iki numunenin birleştirilmiş standart sapmasını hesaplıyoruz:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(47-1)\cdot 12000^2+(55-1)\cdot 18000^2}{47+55-2}}\\[2ex]s_p&=15530,61\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-0308363d68c4677761d44b214b1609d9_l3.png)
Şimdi ortalamalar arasındaki fark için hipotez testi formülünü uyguluyoruz:
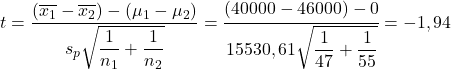
Öte yandan, ortalamalar arasındaki fark için hipotez testinin kritik değerini Öğrenci t tablosunda ararız:
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025| 100}=1,984\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d5f11ecd0336e50c63b0ab2fab4bd530_l3.png)
Daha sonra test istatistiğinin mutlak değeri kritik test değerinden küçük olduğundan sıfır hipotezi kabul edilir ve alternatif hipotez reddedilir.
![]()