Basit doğrusal regresyon

İle Dr.benjamin anderson Ağustos 2, 2023 İstatistik 0 Yorum

Bu makalede istatistikte basit doğrusal regresyonun ne olduğu ve nasıl yapıldığı anlatılmaktadır. Benzer şekilde, çözülmüş basit bir doğrusal regresyon alıştırması ve buna ek olarak çevrimiçi olarak basit bir doğrusal regresyon hesaplayıcısı bulacaksınız.

Basit doğrusal regresyon nedir?

Basit doğrusal regresyon, bağımsız bir değişkeni ilişkilendirmek için kullanılan istatistiksel bir modeldir ve iki değişken arasındaki ilişkiyi yaklaşık olarak tahmin etmeye çalışırız.

Bu nedenle, iki değişkeni doğrusal olarak ilişkilendiren bir denklem bulmak için basit doğrusal regresyon kullanılır. Mantıksal olarak iki değişken arasındaki ilişkinin doğrusal olması gerekir, aksi halde başka tür bir regresyon modelinin kullanılması gerekir.

Basit bir doğrusal regresyon modelinin denklemi iki katsayıdan oluşur: denklemin sabiti (b ₀ ) ve iki değişken arasındaki korelasyon katsayısı (b ₁ ). Bu nedenle, basit bir doğrusal regresyon modelinin denklemi y=b ₀ +b ₁ x’tir.

$y=b_0+b_1x$

Basit bir doğrusal regresyon denklemi düz bir çizgi olarak grafiğe geçirilmiştir, dolayısıyla b ₀ katsayısı kesim noktasıdır ve b ₁ katsayısı da çizginin eğimidir.

Basit doğrusal regresyon formülleri

Basit bir doğrusal regresyonun katsayılarını hesaplamak için formüller aşağıdaki gibidir:

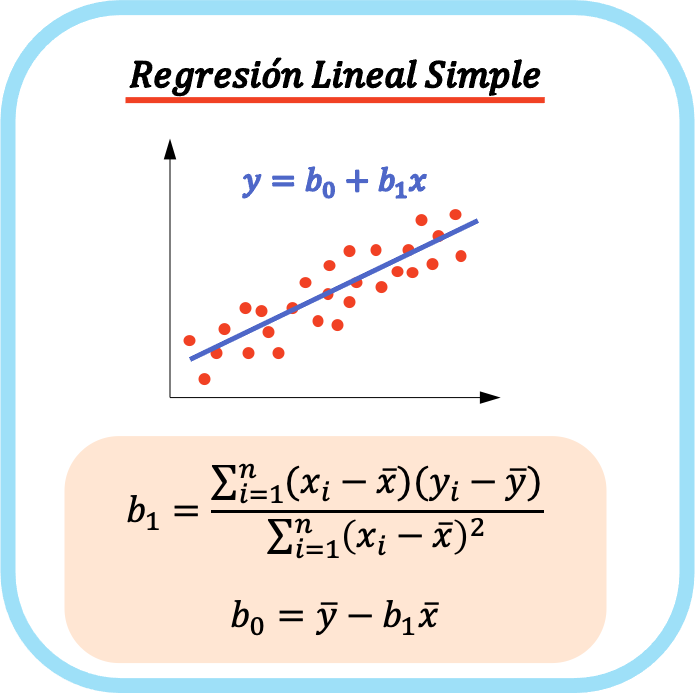
👉Herhangi bir veri seti için basit doğrusal regresyonun katsayılarını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Açıkçası, basit doğrusal regresyon modelinden elde edilen denklem tüm gözlemlerin kesin değerini tahmin edemeyecek çünkü bu model sadece iki değişken arasındaki ilişkiye yaklaşan bir denklem bulmaya çalışıyor. Böylece artık, gerçek değer ile doğrusal regresyon modeliyle tahmin edilen değer arasındaki fark olarak tanımlanır.

$e_i=y_i-\widehat{y}_i$

Basit bir doğrusal regresyon modelinin amacının artıkların karelerini en aza indirmek olduğunu, yani basit doğrusal regresyonun en küçük kareler kriterine dayandığını unutmayın.

Basit doğrusal regresyonun somut örneği

Basit doğrusal regresyon yöntemini anlamayı tamamlamak için, burada basit bir doğrusal regresyon modelinin denkleminin bir dizi istatistiksel veriden hesaplandığı pratik, adım adım bir örnek verilmiştir.

İstatistik sınavına girdikten sonra beş öğrenciye sınava kaç saat çalıştıkları soruldu. Veriler aşağıdaki tabloda sunulmaktadır. Çalışma saatlerini alınan notla doğrusal olarak ilişkilendirmek için toplanan istatistiksel verilerin basit bir doğrusal regresyon modelini gerçekleştirin.

Basit bir doğrusal regresyon modeli gerçekleştirmek için denklemin b ₀ ve b ₁ katsayılarını belirlemeli ve bunun için yukarıdaki bölümde görülen formülleri kullanmalıyız.

Ancak basit doğrusal regresyon formüllerini uygulamak için öncelikle bağımsız değişkenin ortalamasını ve bağımlı değişkenin ortalamasını hesaplamamız gerekir:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Artık değişkenlerin ortalamasını bildiğimize göre, ilgili formülü kullanarak modelin b ₁ katsayısını hesaplıyoruz:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Son olarak, ilgili formülü kullanarak modelin b ₀ katsayısını hesaplıyoruz:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Kısacası problemin basit doğrusal regresyon modelinin denklemi şöyledir:

$y=2,0294+0,4412x$

Aşağıda örnek verilerin grafiksel gösterimini ve basit doğrusal regresyon modelinin düz çizgisini görebilirsiniz:

Son olarak basit doğrusal regresyon modelinin denklemini hesapladıktan sonra geriye kalan tek şey elde edilen sonucu yorumlamaktır. Bunun için regresyon modelinin belirleme katsayısının hesaplanması şarttır, bunun nasıl yapıldığını sitemizde ilgili makaleyi arayarak görebilirsiniz.

Basit Doğrusal Regresyon Varsayımları

Basit bir doğrusal regresyon gerçekleştirmek için aşağıdaki varsayımların karşılanması gerekir:

Bağımsızlık : Gözlenen kalıntılar birbirinden bağımsız olmalıdır. Model bağımsızlığını sağlamanın yaygın bir yolu örnekleme sürecine rastgelelik eklemektir.
Homoskedastisite : Artıkların varyanslarında homojenlik olmalı, yani artıkların değişkenliği sabit olmalıdır.
Normallik : Artıkların normal dağılması veya başka bir deyişle ortalaması 0 olan normal dağılıma uyması gerekir.
Doğrusallık – Bağımsız değişken ile bağımlı değişken arasındaki ilişki doğrusal olmalıdır.

Basit Doğrusal Regresyon Hesaplayıcısı

İki değişken arasında basit bir doğrusal regresyon modeli oluşturmak için aşağıdaki hesap makinesine örnek bir veri ekleyin. Veri çiftlerini ayırmanız gerekir, böylece ilk kutuda yalnızca bağımsız değişken X’in değerleri bulunur ve ikinci kutuda yalnızca bağımlı değişken Y’nin değerleri bulunur.

Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Basit ve çoklu doğrusal regresyon

Son olarak basit doğrusal regresyon ile çoklu doğrusal regresyon arasındaki farkın ne olduğunu göreceğiz çünkü bunlar istatistikte sıklıkla kullanılan iki tür doğrusal regresyondur.

Çoklu doğrusal regresyon, iki veya daha fazla açıklayıcı değişkenin bir yanıt değişkenine matematiksel olarak bağlanmasını mümkün kılar. Yani çoklu doğrusal regresyonda en az iki bağımsız değişkenin olduğu bir model oluşturulur.

Dolayısıyla basit doğrusal regresyon ile çoklu doğrusal regresyon arasındaki fark, bağımsız değişkenlerin sayısıdır. Basit doğrusal regresyonda yalnızca bir bağımsız değişken bulunurken, çoklu doğrusal regresyonda iki veya daha fazla bağımsız değişken vardır.

➤ Bakınız: Çoklu doğrusal regresyon

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil