Alt kareler

İle Dr.benjamin anderson Ağustos 2, 2023 İstatistik 0 Yorum

Bu makale istatistikte en küçük karelerin ne olduğunu, en küçük kareler yönteminin ne olduğunu ve bir regresyon modelinin en küçük kareler kriterine nasıl uyduğunu açıklamaktadır.

En küçük kareler yöntemi nedir?

En küçük kareler yöntemi, bir regresyonun denklemini belirlemek için kullanılan istatistiksel bir yöntemdir. Başka bir deyişle en küçük kareler yöntemi, regresyon denklemi hesaplanırken elde edilen hatayı en aza indirmek için regresyon modelinde kullanılan bir kriterdir.

Somut olarak en küçük kareler yöntemi, artıkların kareleri toplamının en aza indirilmesinden oluşur, başka bir deyişle regresyon modelinin öngördüğü değerler ile gözlenen değerler arasındaki farkların kareleri toplamının en aza indirilmesine dayanır. . . Aşağıda bir regresyon modelinin en küçük kareler kriterine nasıl uyduğunu detaylı olarak göreceğiz.

En küçük kareler yönteminin temel özelliği, gözlenen değerler ile regresyon fonksiyonu arasındaki en uzun mesafelerin en aza indirilmesidir. Diğer regresyon kriterlerinden farklı olarak, en küçük kareler yöntemi, büyük bir sayının karesi küçük bir sayının karesinden çok daha büyük olduğundan, büyük artıkları en aza indirmenin küçük artıklardan daha önemli olduğunu düşünmektedir. sayı.

Tahmin hatası

En küçük kareler kavramını tam olarak anlamak için öncelikle bir regresyon modelinde artıkların ne olduğu konusunda net olmamız gerekir. Bu nedenle aşağıda tahmin hatasının ne olduğunu ve nasıl hesaplandığını göreceğiz.

İstatistikte, artık olarak da adlandırılan tahmin hatası , gerçek değer ile regresyon modelinin uydurduğu değer arasındaki farktır. Dolayısıyla istatistiksel artık şu şekilde hesaplanır:

$e_i=y_i-\widehat{y}_i$

Altın:

$e_i$

i verisinin kalıntısıdır.
$y_i$

i verisinin gerçek değeridir.
$\widehat{y}_i$

i verileri için regresyon modeli tarafından sağlanan değerdir.

Dolayısıyla, bir veri parçasının kalıntısı ne kadar büyük olursa, regresyon modelinin bu veri parçasına uyarlanması o kadar zayıf olur. Dolayısıyla artık ne kadar küçük olursa, gerçek değeri ile tahmin edilen değeri arasındaki mesafe de o kadar küçük olur.

Benzer şekilde, bir verinin kalıntısı pozitifse bu, regresyon modelinin gerçek değerden daha düşük bir değer öngördüğü anlamına gelir. Kalıntının negatif olması ise tahmin edilen değerin gerçek değerden büyük olduğu anlamına gelir.

Hata karelerini en aza indirin

Artık istatistikte kalıntının ne olduğunu bildiğimize göre hata karelerinin nasıl en aza indirildiğini anlamak daha kolay olacaktır.

Bir hatanın karesi, bir artığın karesidir, dolayısıyla bir hatanın karesi, gerçek değer ile ikinin kuvvetine yükseltilmiş regresyon modelinin uydurduğu değer arasındaki farka eşittir.

$e_i^2=(y_i-\widehat{y}_i)^2$

Altın:

$e_i^2$

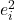
i verisinin kalıntısının karesidir.
$y_i$

i verisinin gerçek değeridir.
$\widehat{y}_i$

i verileri için regresyon modeli tarafından sağlanan değerdir.

Böylece en küçük kareler yöntemi, hataların karelerinin toplamını en aza indirerek bir regresyon modeli oluşturmaktan ibarettir. Bu nedenle en küçük kareler kriteri aşağıdaki ifadenin minimizasyonuna dayanmaktadır:

$\begin{array}{l} [MIN] \ \displaystyle \sum_{i=1}^ne_i^2\\[4ex][MIN] \ \displaystyle \sum_{i=1}^n(y_i-\widehat{y}_i)^2\end{array}$

Bu nedenle en küçük kareler kriterine en küçük kareler kriteri de denilmektedir.

Önceki formülde de görebileceğiniz gibi, en küçük kareler kriteri, küçük artıklardan ziyade büyük kalıntıların minimizasyonuna daha fazla önem vermektedir. Örneğin, bir kalıntı 3 ve diğer bir kalıntı 5 ise, bunların kareleri sırasıyla 9 ve 25 olur, dolayısıyla en küçük kareler kriteri, birinci kalıntıdan önce ikinci kalıntının en aza indirilmesine öncelik verecektir.

En küçük kareler ayarı

En küçük kareler kriterini kullanarak bir regresyon modelinin yerleştirilmesi, artıkların karelerini en aza indiren bir regresyon modelinin bulunmasından oluşur. Bu nedenle regresyon modelinden elde edilen denklem, gözlenen değerler ile uydurulan değerler arasındaki farkların kareleri minimum olan bir denklem olacaktır.

Aşağıdaki örnekte, bir regresyon modeli oluşturmak için daha fazla kriterin bulunduğunu ve seçilen kritere bağlı olarak regresyon denkleminin farklı olduğunu unutmayın.

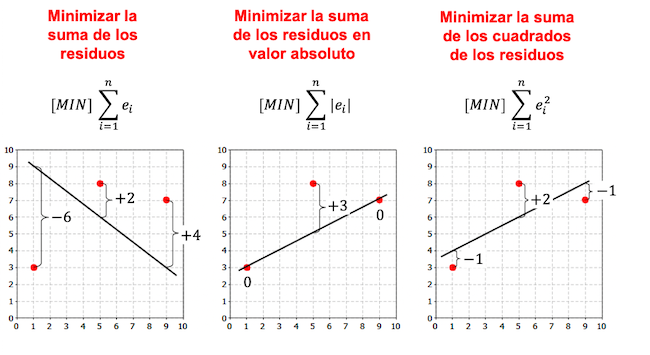
en küçük kareler yöntemi, en küçük kareler ayarlaması

Önceki örneklerde de görüldüğü gibi aynı veri seti için doğrusal regresyon modelinden elde edilen doğru, seçilen kritere bağlıdır. Regresyon modellerinde genel olarak en küçük kareler kriteri kullanılmaktadır.

İstatistikte en yaygın kullanılan regresyon modeli, bağımsız değişken X ile bağımlı değişken Y arasındaki ilişkiyi düz bir çizgi kullanarak tahmin etmekten oluşan basit doğrusal regresyon modelidir.

$y=b_0+b_1x$

Dolayısıyla, bir veri kümesini basit bir doğrusal regresyon modeline sığdırmaya yönelik formüller şunlardır:

$b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}$

$b_0=\overline{y}-b_1\overline{x}$

Basit bir doğrusal regresyon modelinin en küçük kareler kriteri kullanılarak nasıl hesaplandığına dair bir örneği aşağıdaki bağlantıya tıklayarak görebilirsiniz:

➤ Bakınız: Basit doğrusal regresyon örneği

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil