Belirleme katsayısı (r kare)
Bu makale istatistikte belirleme katsayısının (veya R karenin) ne olduğunu açıklamaktadır. Böylece, belirleme katsayısının nasıl hesaplanacağını, nasıl yorumlanacağını ve ayrıca bir veri örneğinin belirleme katsayısını hesaplamak için çevrimiçi bir hesap makinesini öğreneceksiniz.
Belirleme katsayısı nedir (R kare)?
Sembolü R2 ( R kare ) olan belirleme katsayısı , bir regresyon modelinin uyum iyiliğini ölçen bir istatistiktir. Belirleme katsayısı, bir regresyon modelinin bir veri setine ne kadar iyi uyduğunu gösterir, yani regresyon modelinin açıkladığı yüzdeyi gösterir.
Bu nedenle, belirleme katsayısı ne kadar yüksek olursa regresyon modeli o kadar iyi olur. Her ne kadar bu koşul her zaman karşılanamasa da, prensipte mümkün olduğu kadar büyük bir belirleme katsayısıyla ilgileniyoruz. Belirleme katsayısının nasıl yorumlanacağını aşağıda göreceğiz.
Katsayıyı belirleme formülü
Belirleme katsayısı, bağımlı değişkenin artık varyansı ile varyansı arasındaki oranın bir eksisine eşittir. Belirleme katsayısı, toplam kareler toplamı üzerinden artıklardan bir eksi kareler toplamı çıkarılarak da hesaplanabilir.
Dolayısıyla, belirleme katsayısını hesaplama formülü aşağıdaki gibidir:

Altın:
-

belirleme katsayısıdır.
-
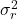
kalan varyanstır.
-

bağımlı değişken Y’nin varyansıdır.
-
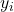
gözlem bağımlı değişkeni i’nin değeridir.
-
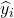
gözlem i için regresyon modeli tarafından yaklaşık olarak tahmin edilen değerdir.
-

tüm gözlemlerdeki bağımlı değişkenin ortalamasıdır.
👉Herhangi bir veri seti için belirleme katsayısını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.
Doğrusal regresyon modeli durumunda, belirleme katsayısı korelasyon katsayısının karesine eşittir:
![]()
Altın
![]()
X ve Y değişkenlerinin kovaryansıdır ,
![]()
Ve
![]()
sırasıyla bağımsız değişken X ve bağımlı değişken Y’nin varyanslarıdır .
Belirleme Katsayısı Hesaplayıcısı
Basit bir doğrusal regresyon modeline uymak ve belirleme katsayısını hesaplamak için aşağıdaki hesap makinesine örnek bir veri ekleyin. Veri çiftlerini ayırmanız gerekir, böylece ilk kutuda yalnızca bağımsız değişken X’in değerleri bulunur ve ikinci kutuda yalnızca bağımlı değişken Y’nin değerleri bulunur.
Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.
Belirleme katsayısının yorumlanması
Bu bölümde determinasyon katsayısının nasıl yorumlanacağını göreceğiz, çünkü daha sonra ne anlama geldiğini bilmiyorsanız determinasyon katsayısının değerini bilmenin bir anlamı yoktur.
Belirleme katsayısının değeri 0 ila 1 arasında değişebilir, ancak genellikle yüzde olarak ifade edilir, yani minimum %0 ve maksimum %100’dür.
Belirleme katsayısının yorumlanmasına ilişkin olarak, değeri ne kadar yüksek olursa, regresyon modelinin veri örneğini daha iyi açıkladığı anlamına gelir. Dolayısıyla belirleme katsayısı 1’e ne kadar yakınsa model o kadar fazla ayarlanacaktır. Öte yandan 0’a yaklaştıkça üretilen regresyon modelinin güvenilirliği de azalacaktır.
Ancak iki regresyon modelini karşılaştırırken regresyon katsayısı daha yüksek olan model her zaman daha iyi değildir. Örneğin, bir regresyon modelinin regresyon katsayısı R 2 = %100 olabilir çünkü modele birçok açıklayıcı değişken eklenmiştir ve bu nedenle tüm gözlemleri mükemmel bir şekilde açıklayabilir. Ancak bu model, regresyon modelini oluşturmak için kullanılmayan yeni bir değer için kesinlikle çok zayıf bir tahminde bulunuyor.
Ortaya çıkan regresyon modelinin önceki varsayımları karşıladığı da unutulmamalıdır. Bu nedenle, çok yüksek belirleme katsayısına sahip bir model, eğer artıkların değişkenliği sabit değilse (homoskedastisite) işe yaramaz.
Ayrıca belirleme katsayısı, açıklayıcı değişkenlerin dahil edilmesini cezalandırmadığı için önemli bir sınır teşkil etmektedir . Mantıksal olarak, bir regresyon modeli ne kadar çok açıklayıcı değişkene sahipse, model o kadar karmaşık olacaktır, ancak gözlemlenen verileri o kadar iyi açıklayacak ve dolayısıyla belirleme katsayısı da o kadar yüksek olacaktır. Ancak düzeltilmiş belirleme katsayısı, modeldeki değişken sayısını dikkate alır (aşağıda nasıl hesaplandığını göreceğiz).
Sonuç olarak, belirleme katsayısı bir regresyon modelini analiz etmek için çok faydalıdır çünkü regresyon modelinin veri setine ne kadar iyi uyduğunu bilmemizi sağlar. Ancak ortaya çıkan modeli incelemek için istatistiksel grafikler gibi başka araçlar da kullanılmalıdır.
Düzeltilmiş belirleme katsayısı
Düzeltilmiş belirleme katsayısı olarak da adlandırılan düzeltilmiş belirleme katsayısı, modele dahil edilen açıklayıcı değişkenlerin sayısını dikkate alarak bir regresyon modelinin uyum iyiliğini ölçer.
Belirleme katsayısı ile düzeltilmiş belirleme katsayısı arasındaki fark, belirleme katsayısının, değişken sayısını dikkate almadan düzeltmenin kalitesini ölçmesi, düzeltilmiş belirleme katsayısının ise düzeltmenin kalitesini ölçmesidir. eklenen her değişken için cezalandırma.
Düzeltilmiş belirleme katsayısının hesaplanmasına yönelik formül aşağıdaki gibidir:
![]()
Altın:
-

düzeltilmiş belirleme katsayısıdır.
-

belirleme katsayısıdır.
-

örneklem büyüklüğüdür.
-

regresyon modelindeki açıklayıcı değişkenlerin sayısıdır.
Bu nedenle, modeller farklı sayıda açıklayıcı değişkene sahip olabileceğinden, düzeltilmiş belirleme katsayısı, iki farklı modelin karşılaştırılmasında belirleme katsayısından daha iyidir.