İstatistikte asimetri nasıl yorumlanır: örneklerle

İstatistikte bir dağılımın simetrisini tanımlamak için çarpıklığı kullanırız.

Veri değerlerinin dağılımının, dağılımın sol tarafında bir “kuyruk” varsa çarpık olduğunu söyleriz:

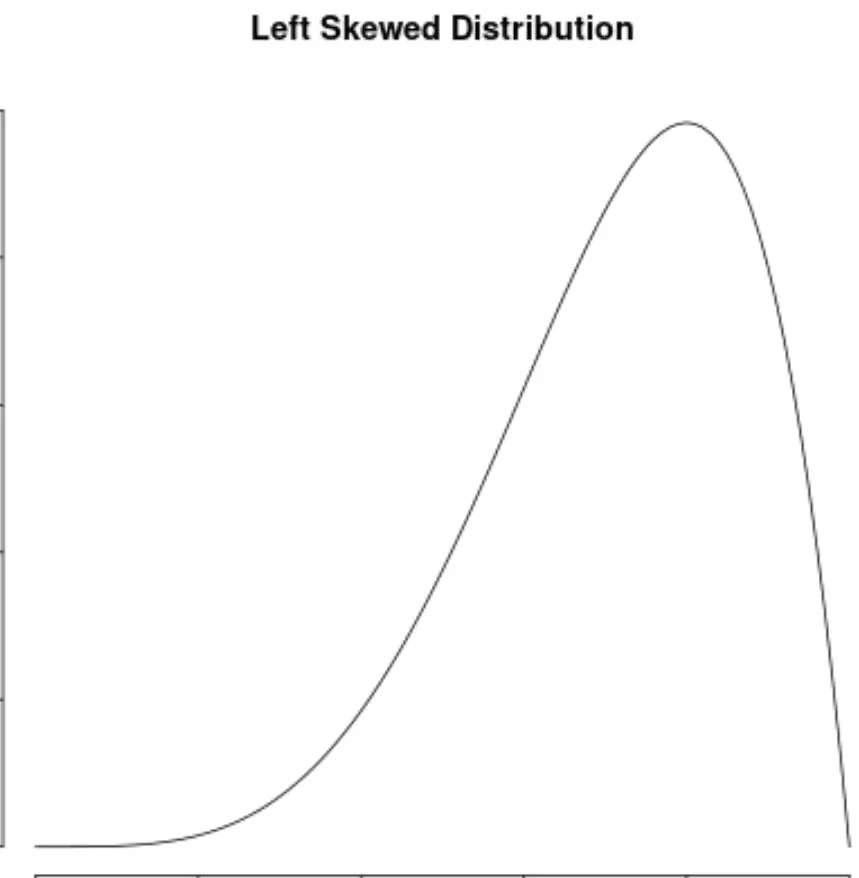
Bir dağılımın sağ tarafında bir “kuyruğu” varsa, bu dağılımın sağa çarpık olduğu söylenir:

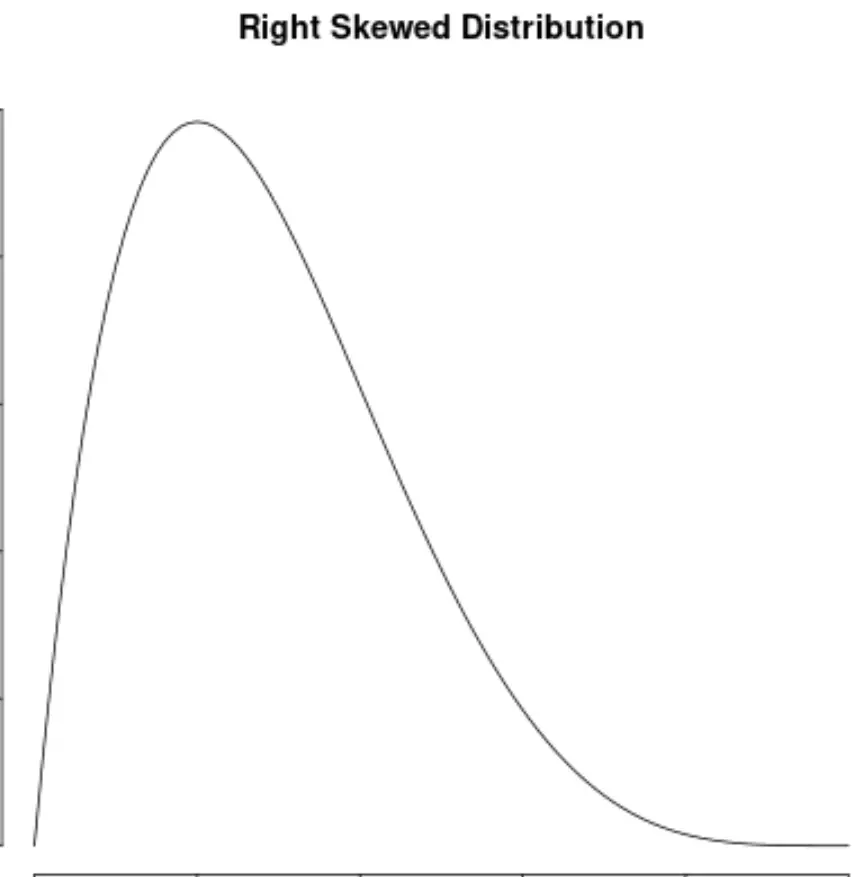
Ve eğer bir dağılım her iki tarafta da simetrikse , asimetrinin olmadığını söylüyoruz:

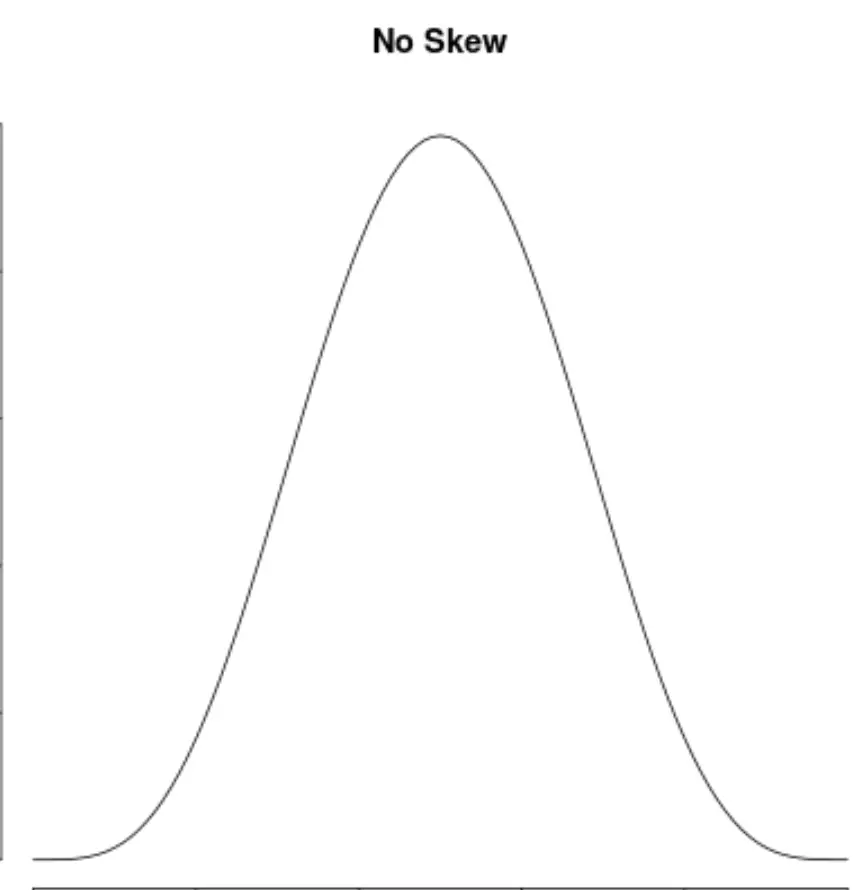
Asimetri nasıl yorumlanır?

Asimetrinin değeri negatif sonsuzdan pozitif sonsuza kadar değişebilir.

Asimetri değerlerini nasıl yorumlayacağınız aşağıda açıklanmıştır:

• Çarpıklık için negatif bir değer, kuyruğun dağılımın sol tarafında olduğunu ve daha negatif değerlere doğru uzandığını gösterir.
• Çarpıklık için pozitif bir değer, kuyruğun dağılımın sağ tarafında olduğunu ve daha pozitif değerlere doğru uzandığını gösterir.
• Sıfır değeri, dağılımda asimetri olmadığını, yani dağılımın tamamen simetrik olduğunu gösterir.

Aşağıdaki örnekler, asimetri değerlerinin pratikte nasıl yorumlanacağını göstermektedir.

Örnek 1: sola çarpık dağılım

Çoğu nüfusta ölümlerin yaş dağılımı sola çarpıktır. Çoğu insan 70 ila 80 yaşları arasında yaşıyor ve gittikçe daha az sayıda insan bu yaşın altında yaşıyor.

Ölüm yaşına ilişkin değerlerin dağılımını görselleştirmek için bir yoğunluk grafiği oluştursaydık şöyle görünebilir:

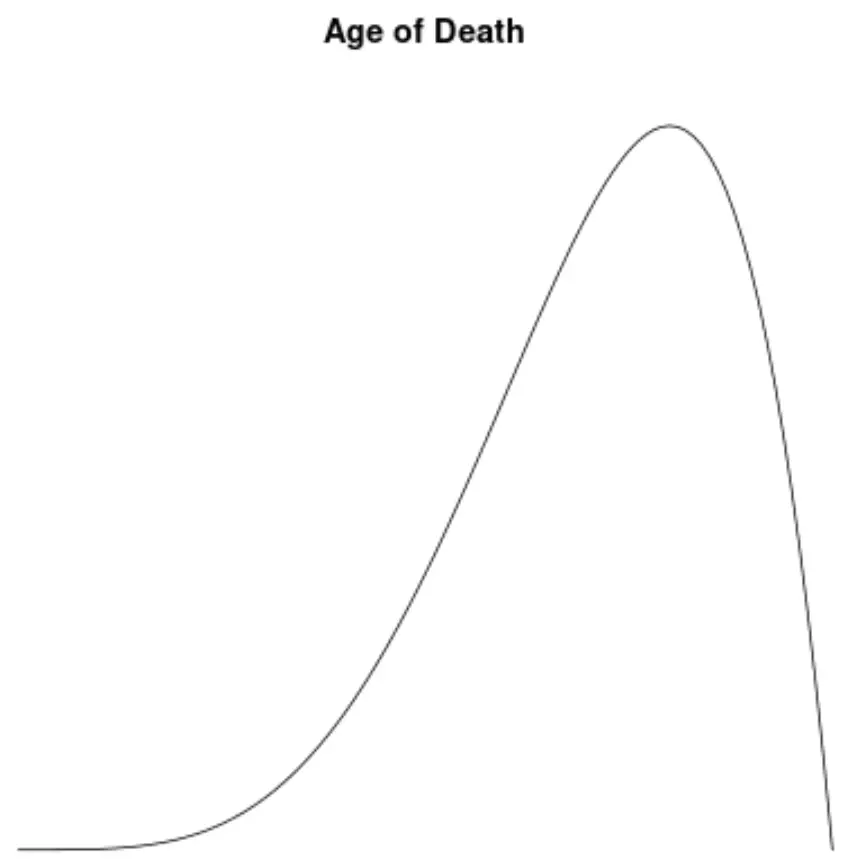
Bu dağılımın çarpıklığını hesapladığımızı ve bunun -1,3225 olduğunu bulduğumuzu varsayalım.

Bu değer negatif olduğu için bunu dağılımın sola çarpık olduğu, yani kuyruğun dağılımın sol tarafına doğru uzandığı şeklinde yorumluyoruz.

Örnek 2: sağa çarpık dağılım

Amerika Birleşik Devletleri’nde hane halkı gelirinin dağılımı sağa çarpıktır; çoğu hane yılda 30.000 ila 70.000 dolar arasında kazanmaktadır, ancak hanelerin uzun sağ kuyruğu çok daha fazla kazanmaktadır.

Hane geliri değerlerinin dağılımını görselleştirmek için bir yoğunluk grafiği oluşturursak şöyle görünebilir:

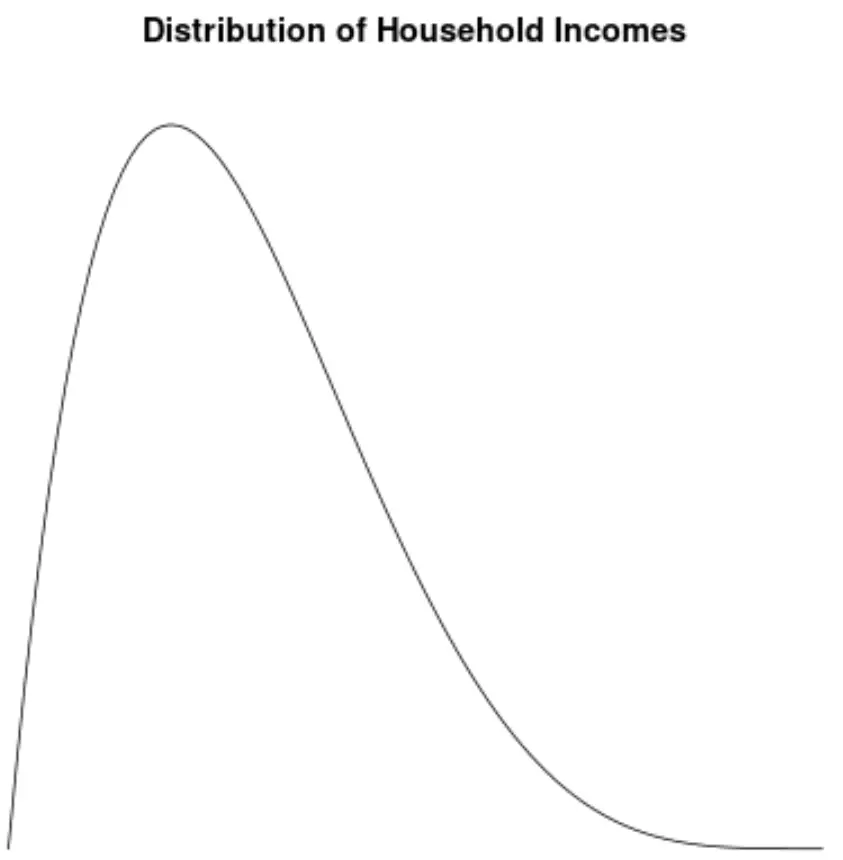
Bu dağılımın çarpıklığını hesapladığımızı ve bunun 2,0043 olduğunu bulduğumuzu varsayalım.

Bu değer pozitif olduğu için bunu dağılımın sağa çarpık olduğu, yani kuyruğun dağılımın sağ tarafına doğru uzandığı şeklinde yorumluyoruz.

Örnek 3: Önyargı yok

Erkeklerin boyutları yaklaşık olarak normal dağılıma sahiptir ve hiçbir asimetri göstermez. Örneğin Amerika Birleşik Devletleri’nde bir erkeğin ortalama boyu yaklaşık 69,1 inçtir. Yükseklik dağılımı kabaca simetriktir; bazıları daha kısa, diğerleri daha uzundur.

Amerika Birleşik Devletleri’nde erkeklerin boy dağılımını görselleştirmek için bir yoğunluk grafiği oluştursaydık, şöyle görünebilir:

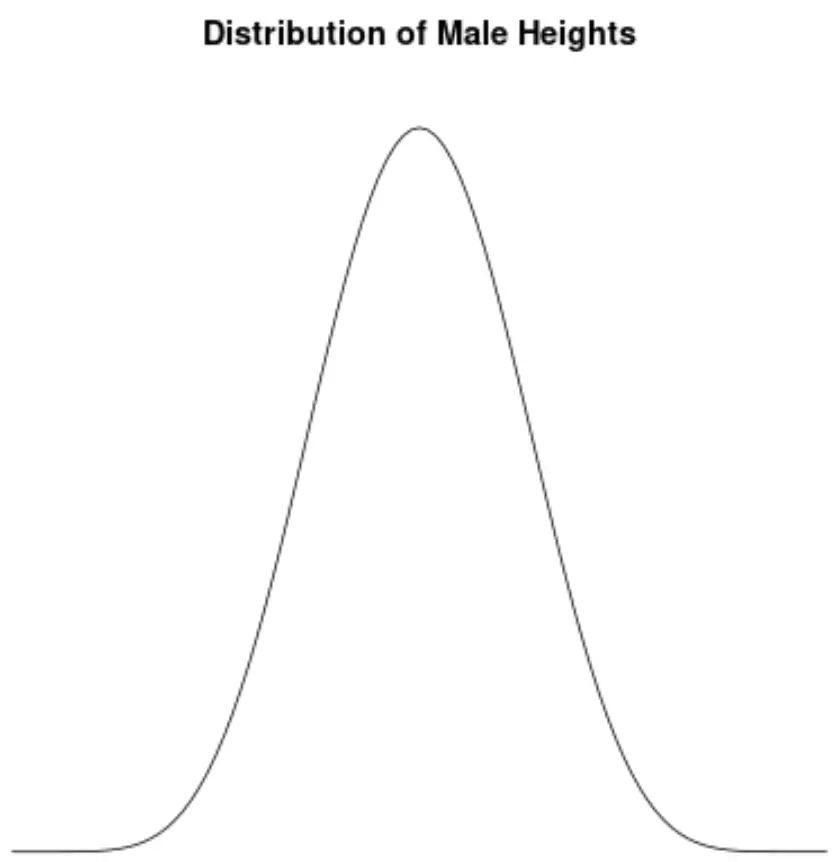
Bu dağılımın çarpıklığını hesapladığımızı ve 0,0013 olduğunu bulduğumuzu varsayalım.

Bu değer sıfıra yakın olduğundan, bunu dağılımın hemen hemen hiç çarpık olmadığı, yani dağılımın her iki tarafındaki kuyrukların yaklaşık olarak eşit olduğu şeklinde yorumluyoruz.

Ek kaynaklar

Aşağıdaki eğitimler eğriltme istatistikleri hakkında ek bilgi sağlar:

Pozitif çarpık dağılımlara 5 örnek
Negatif çarpık dağılımlara 5 örnek
Excel’de Çarpıklık Nasıl Hesaplanır
Kutu Grafiklerinde Asimetri Nasıl Belirlenir?