Eşit olmayan örneklem boyutlarıyla t testi nasıl yapılır?

İstatistik söz konusu olduğunda öğrencilerin sıklıkla sorduğu bir soru şudur:

Her grubun örneklem büyüklükleri eşit olmadığında t testi yapmak mümkün müdür?

Kısa cevap:

Evet, örneklem büyüklükleri eşit olmadığında t testi yapabilirsiniz. Eşit örneklem büyüklüğü, t-testinde yapılan varsayımlardan biri değildir.

Gerçek problemler, t-testinde yapılan varsayımlardan biri olan iki numunenin varyansları eşit olmadığında ortaya çıkar.

Böyle bir durum meydana geldiğinde, eşit varyansları varsaymayan Welch t testinin kullanılması önerilir.

Aşağıdaki örnekler, varyansların eşit olduğu ve olmadığı durumlarda eşit olmayan örneklem büyüklükleriyle T testlerinin nasıl gerçekleştirileceğini göstermektedir.

Örnek 1: Eşit olmayan örneklem boyutları ve eşit varyanslar

Öğrencilerin belirli sınavlarda daha iyi performans göstermelerine yardımcı olmak için tasarlanmış iki program yönettiğimizi varsayalım.

Sonuçlar aşağıdaki gibidir:

Program 1:

• n (örneklem büyüklüğü): 500
• x (örnek ortalama): 80
• s (örnek standart sapması): 5

Program 2:

• n (örneklem büyüklüğü): 20
• x (örnek ortalama): 85
• s (örnek standart sapması): 5

Aşağıdaki kod, her program için sınav puanlarının dağılımını görselleştirmek için R’de bir kutu grafiğinin nasıl oluşturulacağını gösterir:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

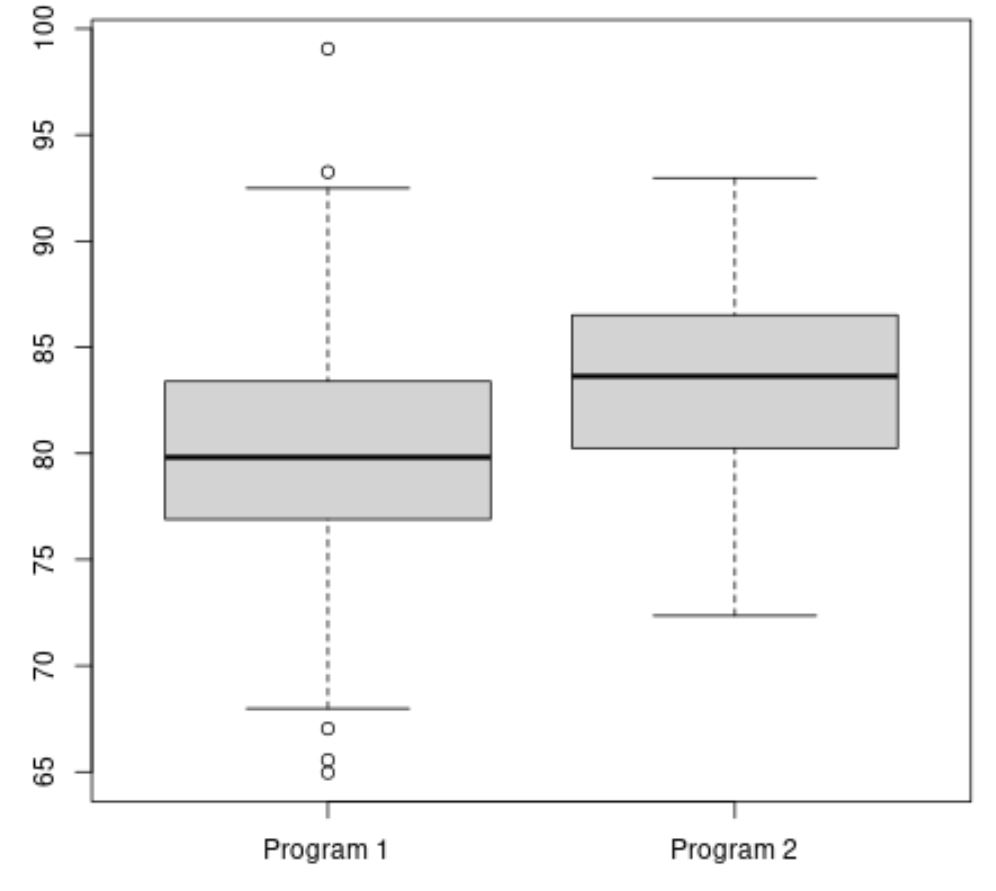
Program 2’nin ortalama sınav puanı daha yüksek görünmektedir ancak iki program arasındaki sınav puanları arasındaki fark yaklaşık olarak eşittir.

Aşağıdaki kod, Welch t testiyle bağımsız örnekler t testinin nasıl gerçekleştirileceğini gösterir:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

Bağımsız örnekler t-testi 0,0009’luk bir p-değeri döndürür ve Welch’in t-testi 0,0029’luk bir p-değeri döndürür.

Her testin p değeri 0,05’ten küçük olduğundan, her testteki sıfır hipotezini reddeder ve iki program arasında ortalama sınav puanlarında istatistiksel olarak anlamlı bir fark olduğu sonucuna varırız.

Örneklem boyutları eşit olmasa da, bağımsız örnekler t-testi ve Welch t-testi, iki örneğin eşit varyanslara sahip olması nedeniyle benzer sonuçlar vermektedir.

Örnek 2: Eşit olmayan örneklem boyutları ve eşit olmayan varyanslar

Öğrencilerin belirli sınavlarda daha iyi performans göstermelerine yardımcı olmak için tasarlanmış iki program yönettiğimizi varsayalım.

Sonuçlar aşağıdaki gibidir:

Program 1:

• n (örneklem büyüklüğü): 500
• x (örnek ortalama): 80
• s (örnek standart sapması): 25

Program 2:

• n (örneklem büyüklüğü): 20
• x (örnek ortalama): 85
• s (örnek standart sapması): 5

Aşağıdaki kod, her program için sınav puanlarının dağılımını görselleştirmek için R’de bir kutu grafiğinin nasıl oluşturulacağını gösterir:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

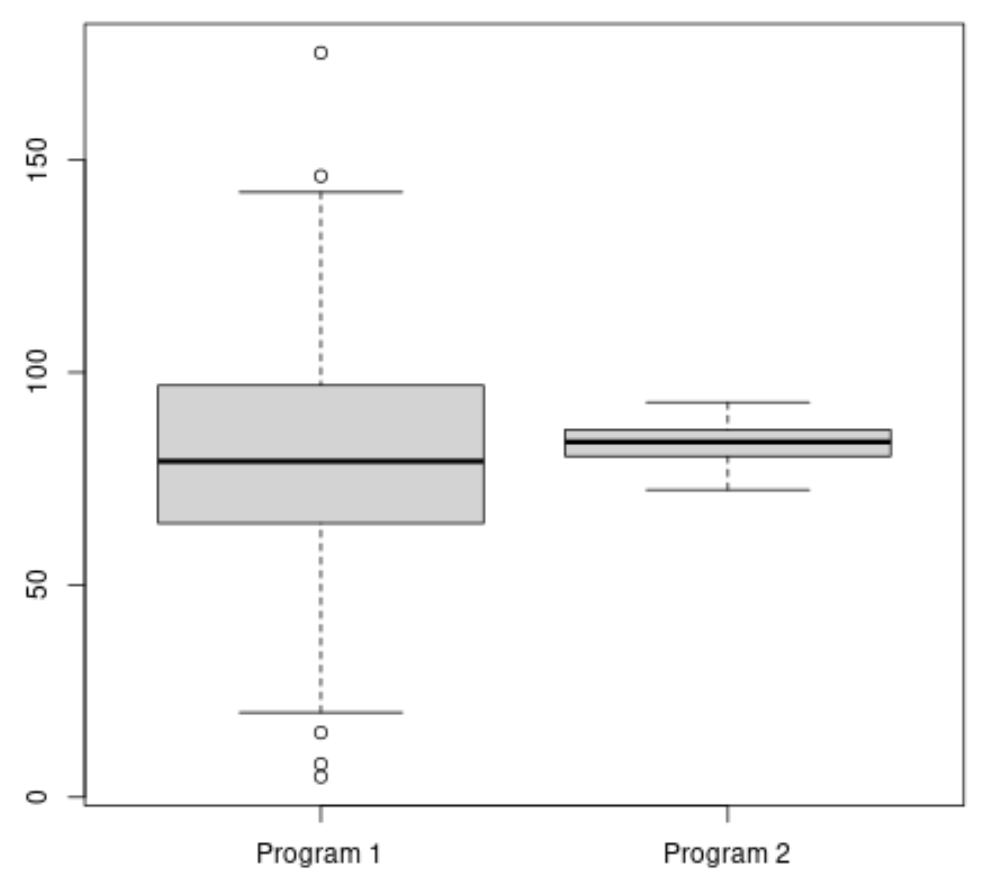
Program 2’nin ortalama sınav puanı daha yüksek görünmektedir, ancak Program 1’in sınav puanlarının varyansı Program 2’den çok daha yüksektir.

Aşağıdaki kod, Welch t testiyle bağımsız örnekler t testinin nasıl gerçekleştirileceğini gösterir:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

Bağımsız örnekler t-testi 0,5496’lık bir p-değeri verir ve Welch’in t-testi 0,0361’lik bir p-değeri verir.

Bağımsız örnekler t testi ortalama sınav puanlarındaki farkı tespit edemez ancak Welch t testi istatistiksel olarak anlamlı bir fark tespit edebilir.

İki numunenin varyansları eşit olmadığından, bu test numuneler arasındaki varyansların eşit olduğunu varsaymadığından yalnızca Welch’in t testi ortalama sınav puanlarındaki istatistiksel olarak anlamlı farkı tespit edebildi .

Ek kaynaklar

Aşağıdaki eğitimler t testleri hakkında ek bilgi sağlar:

Tek örnekli t testine giriş
İki örnekli t testine giriş
Eşleştirilmiş örnekler t-testine giriş