Örnekleme dağılımı nedir?
10.000 yunus popülasyonu olduğunu ve bu popülasyondaki bir yunusun ortalama ağırlığının 300 pound olduğunu düşünün.
Bu popülasyondan 50 yunustan oluşanbasit rastgele bir örnek alırsak, bu örnekteki yunusların ortalama ağırlığının 305 pound olduğunu bulabiliriz.
Daha sonra, 50 yunustan oluşan başka bir basit rastgele örnek alırsak, bu örnekteki yunusların ortalama ağırlığının 295 pound olduğunu bulabiliriz.
Ne zaman 50 yunustan oluşan rastgele bir örnek alsak, örnekteki yunusların ortalama ağırlığının popülasyon ortalaması olan 300 pound’a yakın olması muhtemeldir, ancak tam olarak 300 pound değildir.
Bu popülasyondan 50 yunustan 200 basit rastgele örnek aldığımızı ve her örneğin ortalama ağırlığının bir histogramını oluşturduğumuzu hayal edelim:
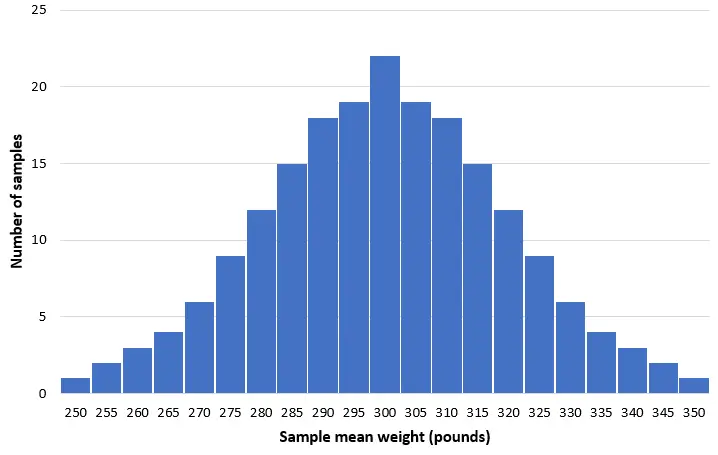
Çoğu numunede ortalama ağırlık 300 pound’a yakın olacaktır. Nadir durumlarda, ortalama ağırlığı yalnızca 250 pound olan küçük yunuslarla dolu bir örnek alabiliriz. Veya ortalama 350 kiloluk şişe burunlu yunuslarla dolu bir örnek alabiliriz. Genel olarak, örneklem ortalamalarının dağılımı yaklaşık olarak normal olacaktır ve dağılımın merkezi popülasyonun gerçek merkezinde yer alacaktır.
Örnek ortalamalarının bu dağılımı , ortalamanın örnekleme dağılımı olarak bilinir ve aşağıdaki özelliklere sahiptir:
µx = µ
burada μ x örnek ortalamasıdır ve μ popülasyon ortalamasıdır.
σx = σ/√n
burada σ x örneklem standart sapması, σ popülasyon standart sapması ve n örneklem büyüklüğüdür.
Örneğin, bu yunus popülasyonunda ortalama ağırlığın μ = 300 olduğunu biliyoruz. Yani örnekleme dağılımının ortalaması μ x = 300 olur.
Ayrıca popülasyon standart sapmasının 18 pound olduğunu bildiğimizi varsayalım. Dolayısıyla numunenin standart sapması σ x = 18/ √50 = 2,546’dır .
Oranın örnekleme dağılımı
Aynı 10.000 yunus popülasyonunu düşünün. Yunusların %10’unun siyah, geri kalanının gri olduğunu varsayalım. 50 yunustan oluşanbasit rastgele bir örnek aldığımızı ve bu örnekteki yunusların %14’ünün siyah olduğunu bulduğumuzu varsayalım. Daha sonra, 50 yunustan oluşan başka bir basit rastgele örnek alıyoruz ve bu örnekteki yunusların %8’inin siyah olduğunu buluyoruz.
Bu popülasyondan 50 yunustan oluşan 200 basit rastgele örnek aldığımızı ve her örnekteki siyah yunusların oranının histogramını oluşturduğumuzu düşünün:
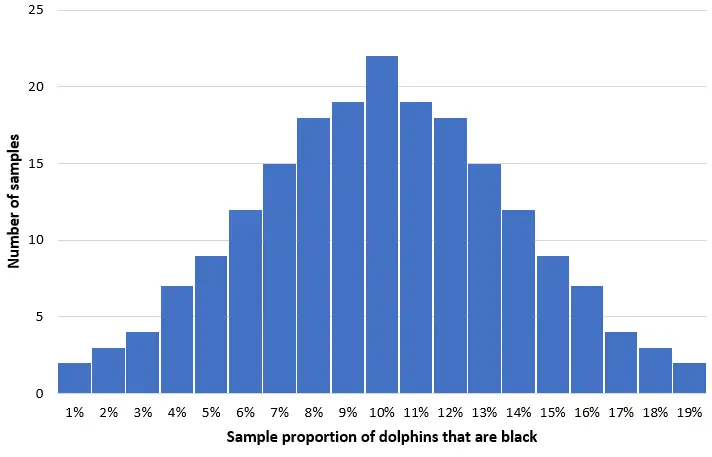
Örneklerin çoğunda siyah yunusların oranı gerçek popülasyon olan %10’a yakın olacaktır. Siyah yunusların örnek oranının dağılımı yaklaşık olarak normal olacaktır ve dağılımın merkezi popülasyonun gerçek merkezinde yer alacaktır.
Örnek oranlarının bu dağılımı, orantı örnekleme dağılımı olarak bilinir ve aşağıdaki özelliklere sahiptir:
µp = P
burada p örnek oranı ve P popülasyon oranıdır.
σ p = √ (P)(1-P) / n
burada P nüfus oranı ve n örneklem büyüklüğüdür.
Örneğin, bu yunus popülasyonunda siyah yunusların gerçek oranının %10 = 0,1 olduğunu biliyoruz. Dolayısıyla orantısal örnekleme dağılımının ortalaması μ p = 0,1’dir .
Ayrıca popülasyon standart sapmasının 18 pound olduğunu bildiğimizi varsayalım. Böylece örneklemin standart sapması σ p = √ (P)(1-P) / n = √ (.1)(1-.1) / 50 = .042 olur.
Normalliği tesis edin
Yukarıdaki formülleri kullanabilmek için örnekleme dağılımının normal olması gerekir.
Merkezi limit teoremine göre, popülasyon dağılımı normal olmasa bile, örneklem büyüklüğü yeterince büyükse, bir örneklem ortalamasının örnekleme dağılımı yaklaşık olarak normaldir. Çoğu durumda, 30 veya daha fazla örneklem büyüklüğünün yeterince büyük olduğunu düşünüyoruz.
Beklenen başarı ve başarısızlık sayısı en az 10 ise, bir numune oranının örnekleme dağılımı yaklaşık olarak normaldir.
Örnekler
Olasılıkları hesaplamak için örnekleme dağılımlarını kullanabiliriz.
Örnek 1: Belirli bir makine çerezler oluşturur. Bu kurabiyelerin ağırlık dağılımı, ortalama 10 ons ve standart sapma 2 ons olacak şekilde sağa çarpıktır. Bu makine tarafından üretilen 100 kurabiyeden oluşan basit rastgele bir örnek alırsak, bu örnekteki kurabiyelerin ortalama ağırlığının 9,8 onstan az olma olasılığı nedir?
Adım 1: Normalliği sağlayın.
Örnek ortalamalarının örnekleme dağılımının normal olduğundan emin olmamız gerekir. Örneklem büyüklüğümüz 30’dan büyük veya 30’a eşit olduğundan, merkezi limit teoremine göre örnek ortalamalarının örnekleme dağılımının normal olduğunu varsayabiliriz.
Adım 2: Örnekleme dağılımının ortalamasını ve standart sapmasını bulun.
µx = µ
σx = σ/√n
μ x = 10 ons
σ x = 2/ √100 = 2/10 = 0,2 ons
Adım 3: Bu örnekteki ortalama kurabiye ağırlığının 9,8 onstan az olma olasılığını belirlemek için Z-Score Alan Hesaplayıcısını kullanın.
Aşağıdaki sayıları Z Puanı Alanı Hesaplayıcısına girin. Bu örnekte yalnızca bir sayı bulduğumuz için “Ham Skor 2″yi boş bırakabilirsiniz.
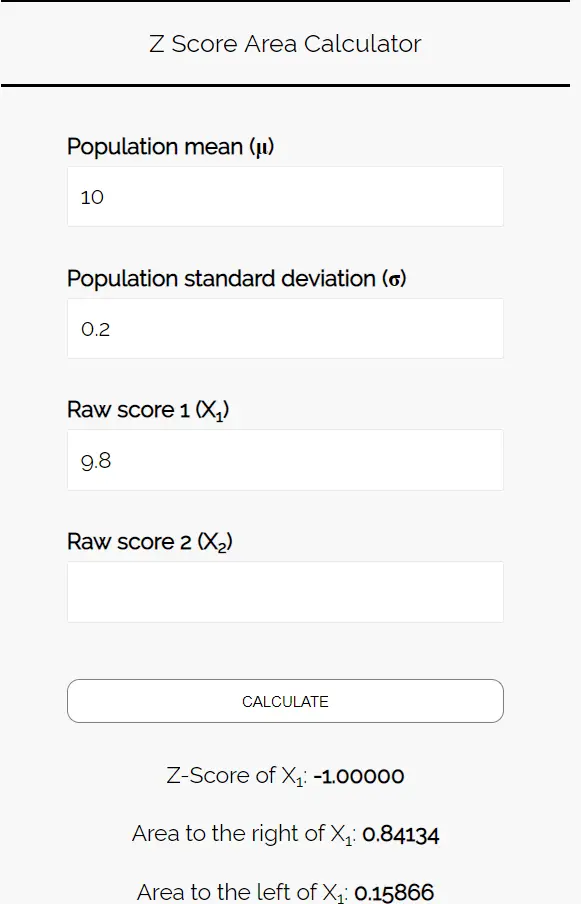
Bu örnekteki kurabiyelerin ortalama ağırlığının 9,8 onstan az olma olasılığını bilmek istediğimiz için soldaki 9,8 onsluk alanla ilgileniyoruz. Hesap makinesi bize bu olasılığın 0,15866 olduğunu söylüyor.
Örnek 2: Okul çapında yapılan bir araştırmaya göre, belirli bir okuldaki öğrencilerin %87’si pizzayı dondurmaya tercih ediyor. 200 öğrenciden oluşan basit rastgele bir örnek aldığımızı varsayalım. Pizza tercih eden öğrencilerin oranının %85’ten az olma olasılığı nedir?
Adım 1: Normalliği sağlayın.
Beklenen “başarı” ve “başarısızlık” sayısı en az 10 ise, bir numune oranının örnekleme dağılımının yaklaşık olarak normal olduğunu hatırlayın.
Bu durumda pizzayı tercih etmesi beklenen öğrenci sayısı %87 * 200 öğrenci = 174 öğrencidir. Pizza tercih etmeyecek öğrenci sayısı ise %13 * 200 öğrenci = 26 öğrencidir. Bu sayıların her ikisi de en az 10 olduğundan pizzayı tercih edecek öğrenci oranının örneklem dağılımının yaklaşık olarak normal olduğunu varsayabiliriz.
Adım 2: Örnekleme dağılımının ortalamasını ve standart sapmasını bulun.
µp = P
σ p = √ (P)(1-P) / n
µp = 0,87
σ p = √ (0,87)(1-0,87) / 200 = 0,024
Adım 3: Pizza tercih eden öğrencilerin oranının %85’ten az olma olasılığını belirlemek için Z-Score Alan Hesaplayıcısını kullanın.
Aşağıdaki sayıları Z Puanı Alanı Hesaplayıcısına girin. Bu örnekte yalnızca bir sayı bulduğumuz için “Ham Skor 2″yi boş bırakabilirsiniz.
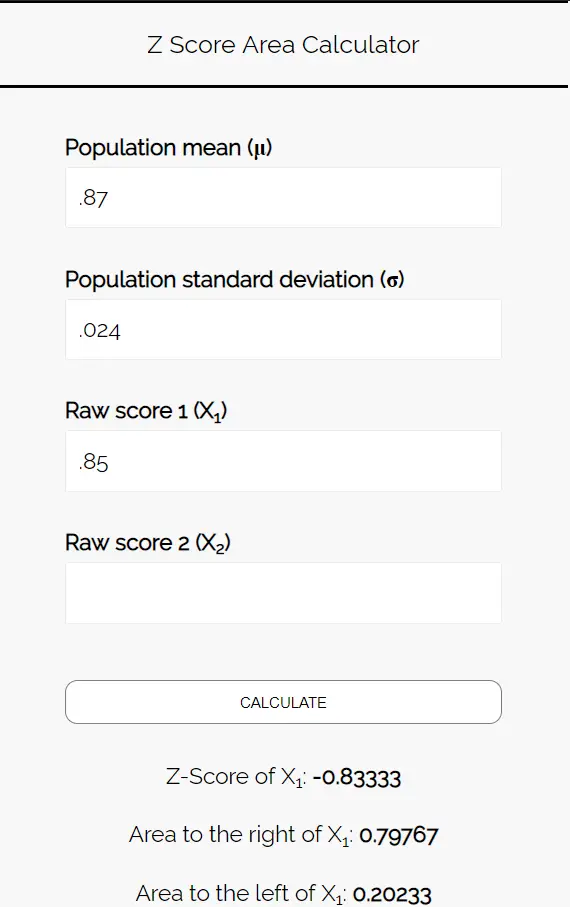
Pizza tercih eden öğrencilerin oranının %85’ten az olma olasılığını bilmek istediğimiz için 0,85’in solundaki alanla ilgileniyoruz. Hesap makinesi bize bu olasılığın 0,20233 olduğunu söylüyor.