Basit doğrusal regresyona giriş

Basit doğrusal regresyon, iki değişken (x ve y) arasındaki ilişkiyi anlamak için kullanabileceğiniz istatistiksel bir yöntemdir.

Bir değişken olan x , yordayıcı değişken olarak bilinir.

Diğer değişken, y , yanıt değişkeni olarak bilinir.

Örneğin, yedi kişinin ağırlığını ve boyunu içeren aşağıdaki veri setine sahip olduğumuzu varsayalım:

Ağırlık belirleyici değişken olsun ve boy da yanıt değişkeni olsun.

Bu iki değişkeni, x ekseninde ağırlık ve y ekseninde yükseklik olacak şekilde bir dağılım grafiği kullanarak grafiklendirirsek, şöyle görünecektir:

Ağırlık ve boy arasındaki ilişkiyi anlamak istediğimizi varsayalım. Dağılım grafiğinden, ağırlık arttıkça boyun da artma eğiliminde olduğunu açıkça görebiliriz, ancak ağırlık ile boy arasındaki bu ilişkiyi gerçekte ölçmek için doğrusal regresyon kullanmamız gerekir.

Doğrusal regresyon kullanarak verilerimize en iyi “uyan” çizgiyi bulabiliriz. Bu çizgi en küçük kareler regresyon çizgisi olarak bilinir ve ağırlık ile boy arasındaki ilişkileri anlamamıza yardımcı olmak için kullanılabilir.

Genellikle bu doğrunun denklemini bulmak için Microsoft Excel, SPSS gibi yazılımları veya grafik hesap makinesini kullanırsınız.

En iyi uyum çizgisinin formülü yazılmıştır:

ŷ = b ₀ + b ₁ x

burada ŷ yanıt değişkeninin tahmin edilen değeridir, b ₀ kesişme noktasıdır, b ₁ regresyon katsayısıdır ve x yordayıcı değişkenin değeridir.

İlgili: Gerçek Hayatta Doğrusal Regresyonun Kullanımına İlişkin 4 Örnek

“En uygun seriyi” bulun

Bu örnek için, verilerimizi istatistiksel doğrusal regresyon hesaplayıcısına bağlayıp Hesapla tuşuna basabiliriz:

Hesap makinesi en küçük kareler regresyon çizgisini otomatik olarak bulur:

ŷ = 32,7830 + 0,2001x

Önceki dağılım grafiğimizden uzaklaşıp bu çizgiyi grafiğe eklersek, şöyle görünecektir:

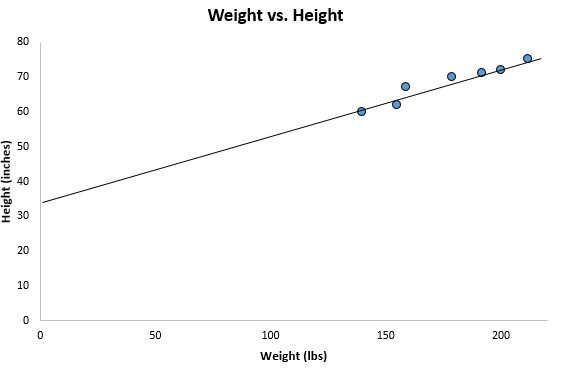
Veri noktalarımızın bu çizgi etrafında nasıl da yakın bir şekilde dağıldığına dikkat edin. Aslında bu en küçük kareler regresyon çizgisi, çizebileceğimiz tüm olası çizgiler arasında verilerimize en uygun olanıdır.

En küçük kareler regresyon çizgisi nasıl yorumlanır

Bu en küçük kareler regresyon çizgisini şu şekilde yorumlayabilirsiniz: ŷ = 32,7830 + 0,2001x

_b0 = 32,7830 . Bu, tahmin değişken ağırlığı sıfır pound olduğunda tahmin edilen yüksekliğin 32,7830 inç olduğu anlamına gelir. Bazen b _0’ın değerini bilmek yararlı olabilir, ancak bu özel örnekte bir kişi sıfır pound ağırlığında olamayacağından b _0’ı yorumlamanın bir anlamı yoktur.

_b1 = 0,2001 . Bu, x’teki bir birimlik artışın, y’deki 0,2001 birimlik artışla ilişkili olduğu anlamına gelir. Bu durumda ağırlıktaki bir poundluk artış, boyda 0,2001 inçlik bir artışla ilişkilidir.

En küçük kareler regresyon çizgisi nasıl kullanılır?

Bu en küçük kareler regresyon çizgisini kullanarak aşağıdaki gibi soruları yanıtlayabiliriz:

170 kilo ağırlığındaki birinin boyunun ne kadar olmasını beklemeliyiz?

Bu soruyu cevaplamak için, x için regresyon çizgimize 170’i ekleyip y’yi çözebiliriz:

ŷ = 32,7830 + 0,2001(170) = 66,8 inç

150 kilo ağırlığındaki birinin boyunun ne kadar olmasını beklemeliyiz?

Bu soruyu cevaplamak için regresyon çizgimize x için 150 ekleyebilir ve y’yi çözebiliriz:

ŷ = 32,7830 + 0,2001(150) = 62,798 inç

Dikkat: Bunun gibi soruları yanıtlamak için regresyon denklemi kullanırken, yordayıcı değişken için yalnızca veri kümesindeki yordayıcı değişkenin aralığı içindeki değerleri kullandığınızdan emin olun. En küçük kareler regresyon çizgisini oluşturmak için kullandığımız orijin. Örneğin veri setimizdeki ağırlıklar 140 ila 212 pound arasında değişiyordu. Bu nedenle, ağırlık 140 ila 212 pound arasında olduğunda beklenen boyla ilgili soruları yanıtlamak mantıklı olur.

Belirleme katsayısı

En küçük kareler regresyon çizgisinin verilere ne kadar iyi uyduğunu ölçmenin bir yolu, ^R2 ile gösterilen belirleme katsayısını kullanmaktır.

Belirleme katsayısı, yordayıcı değişken tarafından açıklanabilen yanıt değişkenindeki varyansın oranıdır.

Belirleme katsayısı 0 ila 1 arasında değişebilir. 0 değeri, yanıt değişkeninin yordayıcı değişken tarafından hiçbir şekilde açıklanamayacağını gösterir. 1 değeri, yanıt değişkeninin yordayıcı değişken tarafından hatasız olarak mükemmel bir şekilde açıklanabileceğini gösterir.

0 ile 1 arasındaki bir ^R2, yanıt değişkeninin yordayıcı değişken tarafından ne ölçüde açıklanabileceğini gösterir. Örneğin, 0,2’lik bir ^R2 , yanıt değişkenindeki varyansın %20’sinin yordayıcı değişken tarafından açıklanabileceğini gösterir; 0,77’lik bir ^R2, yanıt değişkenindeki varyansın %77’sinin yordayıcı değişken tarafından açıklanabileceğini gösterir.

Önceki sonucumuzda 0,9311’lik bir ^R2 elde ettiğimize dikkat edin; bu, boydaki değişkenliğin %93,11’inin ağırlık belirleyici değişken tarafından açıklanabileceğini gösterir:

Bu bize ağırlığın boy için çok iyi bir gösterge olduğunu söyler.

Doğrusal Regresyon Varsayımları

Doğrusal regresyon modelinin sonuçlarının geçerli ve güvenilir olması için aşağıdaki dört varsayımın karşılandığını doğrulamamız gerekir:

1. Doğrusal ilişki: Bağımsız değişken x ile bağımlı değişken y arasında doğrusal bir ilişki vardır.

2. Bağımsızlık: Artıklar bağımsızdır. Özellikle zaman serisi verilerinde ardışık artıklar arasında bir korelasyon yoktur.

3. Homoskedastisite: Artıklar x’in her seviyesinde sabit bir varyansa sahiptir.

4. Normallik: Model artıkları normal dağılıma sahiptir.

Bu varsayımlardan bir veya daha fazlası karşılanmazsa, doğrusal regresyonumuzun sonuçları güvenilmez ve hatta yanıltıcı olabilir.

Her bir varsayımın açıklaması, varsayımın karşılanıp karşılanmadığının nasıl belirleneceği ve varsayım karşılanmazsa ne yapılacağı hakkında bilgi için bu makaleye bakın.