Deneysel olasılık

Burada deneysel olasılığın anlamını ve deneysel olasılığın nasıl hesaplandığını bulacaksınız. Ek olarak, deneysel olasılığı hesaplamanın adım adım çözülmüş bir örneğini görebileceksiniz.

Deneysel olasılık nedir?

Deneysel olasılık, bir deneyin sonuçlarına veya ampirik gerçeklere dayanan istatistiksel bir ölçümdür ve bir olayın meydana gelme olasılığını gösterir.

Ayrıca deney ne kadar çok tekrarlanırsa elde edilen deneysel olasılık o kadar kesin olacaktır. Bu nedenle deneysel olasılığın belirlenmesinde genellikle binlerce deneyi hızlı bir şekilde simüle edebilen bilgisayar programları kullanılır ve böylece daha iyi kesinlik elde edilir.

Deneysel olasılık aynı zamanda ampirik olasılık veya frekans olasılığı olarak da bilinir.

Deneysel olasılık 0 ile 1 arasında bir sayıdır. Mantıksal olarak, bir olayın deneysel olasılığının değeri ne kadar büyükse, gerçekleşme olasılığı da o kadar yüksek olur; bunun tersi de, değer ne kadar küçükse, gerçekleşme olasılığı da o kadar azdır. meydana gelmesi muhtemeldir. veya olay meydana gelir. Ancak deneysel olasılığın değeri her zaman sıfır ile bir arasında olacaktır.

Deneysel olasılık formülü

Deneysel olasılık formülü , bir deney sırasında bir olayın meydana gelme sayısının deneyin gerçekleştirilme toplam sayısına bölünmesiyle elde edilir.

Örneğin, bir kişi bir hedefe 10 dart atar ve merkezdeki 6 dartı vurmayı başarırsa, o kişinin dartı merkezden vurma olasılığı şu şekilde hesaplanır:

Deneysel olasılık örneği

Deneysel olasılığın matematiksel tanımını gördükten sonra, bu tür olasılığa ilişkin adım adım bir alıştırmayı çözeceğiz. Amaç bir olayın deneysel olasılığının nasıl hesaplandığını öğrenmenizdir, dolayısıyla sorularınız varsa yorumlara yazabilirsiniz.

• Bir zarın atılmasıyla ilgili rastgele deneyini oluşturan temel olayların deneysel olasılığını hesaplayın.

Deneysel olasılığı bulmadan önce, elde edilen deneysel sonuçları teorik sonuçlarla karşılaştırmak için teorik olasılığı hesaplayacağız. Bildiğiniz gibi, bir zar atıldığında altı olası sonuç vardır (1, 2, 3, 4, 5 ve 6), dolayısıyla her temel olayın teorik olasılığı şöyledir:

Bu alıştırmayı çözmek için, bir zarın birkaç kez atılmasını simüle etmemiz ve sonuçları bir olasılık tablosuna kaydetmemiz gerekir. Bu durumda simülasyonları Excel programı ile yapacağız ancak siz tabi ki istediğiniz programı kullanabilirsiniz.

Önce on atış, sonra yüz atış ve son olarak da bin atış simülasyonu yapacağız. Bu şekilde sonuçları analiz edebileceğiz ve deneyin örneklem büyüklüğüne bağlı olarak nasıl değiştiğini görebileceğiz. 10 zar atışının rastgele simülasyonundan sonra elde edilen sonuçlar aşağıdaki gibidir:

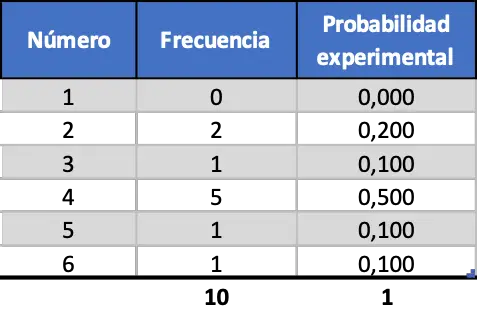
Gördüğünüz gibi elde edilen deneysel olasılıklar, daha önce hesaplanan teorik olasılıklardan (0,167) oldukça farklı.

Ancak test sayısını artırdıkça bu iki ölçüm daha da benzer hale geliyor, 100 fırlatma simülasyonuna bir göz atın:

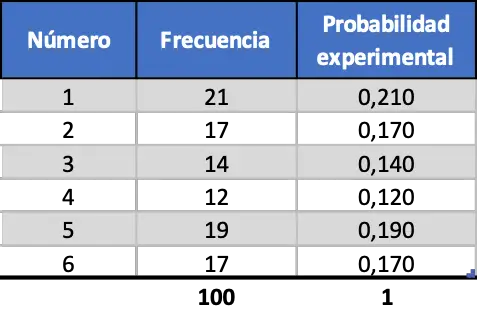
Artık deneysel olasılık daha çok teorik olasılık değerine benziyor ancak yine de uzak değerler elde ediyoruz.

Son olarak aynı işlemi yapıyoruz ancak 1000 başlatmayı simüle ediyoruz:

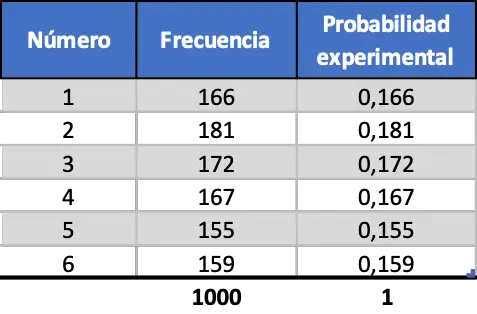
Son beklenmedik durum tablosunda da görebileceğiniz gibi artık deneysel olasılıkların değerleri teorik olasılıklara çok benzer.

Özetle, gerçekleştirilen deney sayısı ne kadar fazla olursa, bir olayın deneysel olasılığının değeri o olayın teorik olasılığına o kadar yakın olacaktır . Bu kural, ne kadar çok veri varsa deneysel değerlerin teorik değerlere o kadar yakın olacağını ifade eden büyük sayılar kanunu olarak tanımlanır.

Aynı şekilde üç frekans tablosunu karşılaştırırsanız deneysel olasılığın kesin olmadığını, yapılan deney sayısına bağlı olarak geliştiğini göreceksiniz. Bu, elde edilen değerleri nasıl yorumlayacağınızı bilmeniz gerektiği anlamına gelir.

Deneysel olasılık ve teorik olasılık

Deneysel olasılık ile teorik olasılık (veya klasik olasılık) arasındaki fark , deneysel olasılığın gerçek bir deneyden toplanan verilerden hesaplanması, teorik olasılığın ise herhangi bir deney yapılmasına gerek kalmadan hesaplanmasıdır.

Gördüğümüz gibi bir olayın deneysel olasılığını ortaya çıkarmak için çok sayıda deneyi simüle etmemiz gerekir. Ancak teorik olasılığı hesaplamak teori ve mantıkla ilgilidir. Burada nasıl yapıldığını görebilirsiniz: