F dağılımını kullanarak güven aralığı nasıl oluşturulur

İki popülasyonun varyanslarının eşit olup olmadığını belirlemek için, σ ² ₁ / σ ² ₂ varyans oranını hesaplayabiliriz; burada σ ² ₁ , popülasyon 1’in varyansı ve σ ² _2, popülasyon 2’nin varyansıdır.

Gerçek popülasyon varyans oranını tahmin etmek için, genellikle her popülasyondan basit rastgele bir örnek alırız ve örnek varyans oranını hesaplarız, s ₁ ² / s ₂ ² ; burada s ₁ ² ve s ₂ ² , örnek 1 ve örnek için örnek varyanslardır. . sırasıyla 2.

Bu test, _s12 ve _s22’nin ^, her ikisi de normal dağılım gösteren popülasyonlardan ^olan , _n1 ve _n2 büyüklüğündeki bağımsız örneklerden hesaplandığını varsayar.

Bu oran birden ne kadar uzaklaşırsa, popülasyon içindeki eşit olmayan varyansların kanıtı o kadar güçlü olur.

σ ² ₁ / σ ² ₂ için (1-α)%100 güven aralığı şu şekilde tanımlanır:

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

burada F _{n 2 -1, n 1 -1, α/2} ve F _{n 1 -1, n 2 -1, α/2}   seçilen önem seviyesi α için F dağılımının kritik değerleridir.

Aşağıdaki örnekler, üç farklı yöntem kullanılarak σ ² ₁ / σ ² ₂ için bir güven aralığının nasıl oluşturulacağını göstermektedir:

• El ile
• Microsoft Excel’i kullanın
• R istatistik yazılımının kullanımı

Aşağıdaki örneklerin her biri için aşağıdaki bilgileri kullanacağız:

• a = 0,05
• _n1 = 16
• _n2 = 11
• s ₁ ² =28,2
• s ₂ ² = 19,3

Manuel olarak bir güven aralığı oluşturma

σ ² ₁ / σ ² ₂ için bir güven aralığını manuel olarak hesaplamak için elimizdeki sayıları güven aralığı formülüne yerleştireceğiz:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, a/2}

Eksik olduğumuz tek rakamlar kritik değerlerdir. Neyse ki bu kritik değerleri F dağıtım tablosunda bulabiliriz:

F _{n2-1, n1-1, α/2} = F _{10, 15, 0,025} = 3,0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0,025} = 1 / 3,5217 = 0,2839

(Tabloyu yakınlaştırmak için tıklayın)

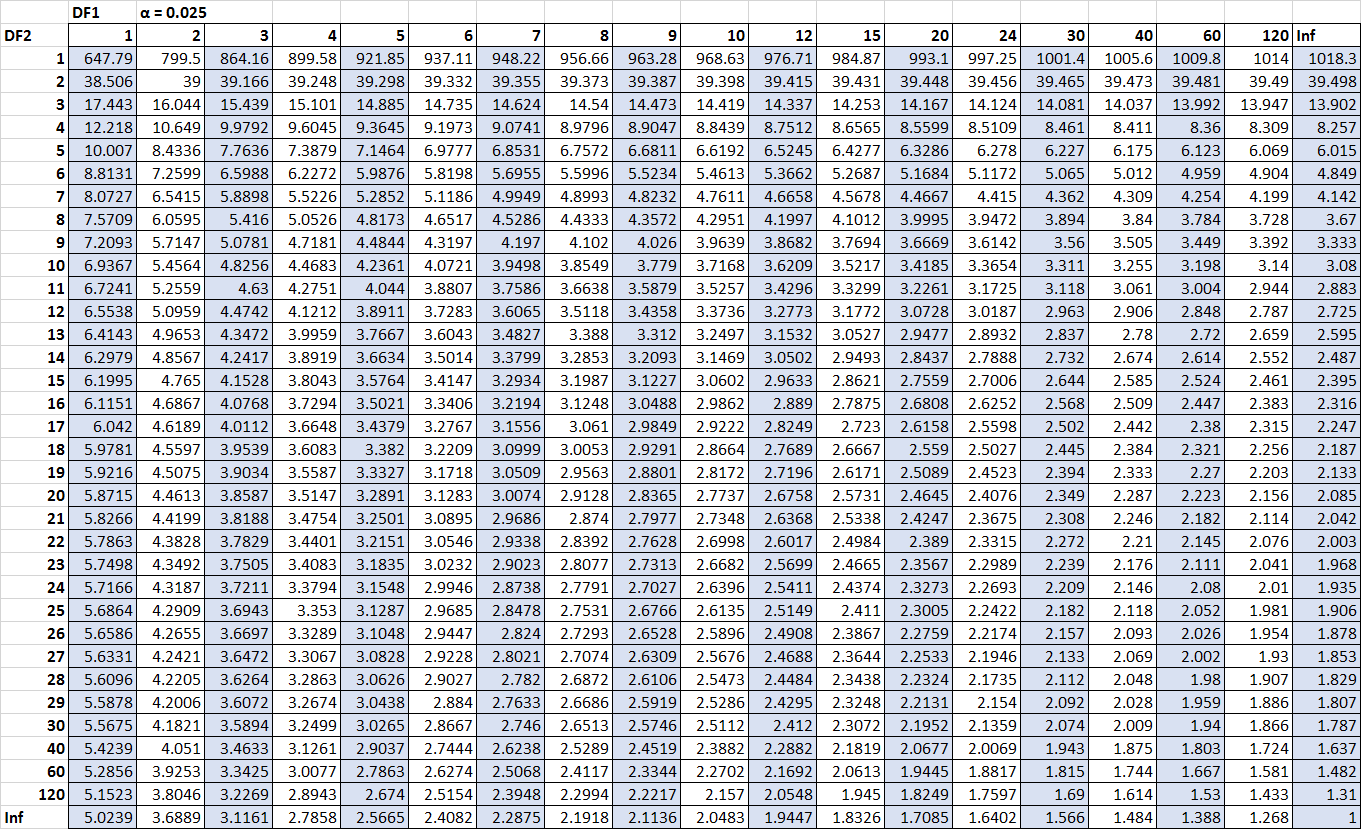
Artık tüm sayıları güven formülü aralığına yerleştirebiliriz:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, a/2}

(28,2 / 19,3) * (0,2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28,2 / 19,3) * (3,0602)

0,4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4,4714

Dolayısıyla ana kütle varyanslarının oranı için %95 güven aralığı (0,4148, 4,4714)’ tir.

Excel Kullanarak Güven Aralığı Oluşturma

Aşağıdaki görüntü, Excel’de popülasyon varyans oranı için %95 güven aralığının nasıl hesaplanacağını gösterir. Güven aralığının alt ve üst sınırları E sütununda, alt ve üst sınırları bulmak için kullanılan formül ise F sütununda gösterilmiştir:

Dolayısıyla ana kütle varyanslarının oranı için %95 güven aralığı (0,4148, 4,4714)’ tir. Bu, güven aralığını manuel olarak hesapladığımızda elde ettiğimiz sonuçla eşleşiyor.

R Kullanarak Güven Aralığı Oluşturma

Aşağıdaki kod, R’deki popülasyon varyanslarının oranı için %95 güven aralığının nasıl hesaplanacağını gösterir:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Dolayısıyla ana kütle varyanslarının oranı için %95 güven aralığı (0,4148, 4,4714)’ tir. Bu, güven aralığını manuel olarak hesapladığımızda elde ettiğimiz sonuçla eşleşiyor.

Ek kaynaklar

F dağıtım panosu nasıl okunur
Excel’de kritik F değeri nasıl bulunur?