T testinden p değerini manuel olarak hesaplama

İstatistikte en yaygın kullanılan testlerden biri, bir popülasyonun ortalamasının belirli bir değere eşit olup olmadığını belirlemek için sıklıkla kullanılan t testidir .

Örneğin belirli bir bitki türünün ortalama boyunun 15 inç olup olmadığını bilmek istediğimizi varsayalım. Bunu test etmek için 20 bitkiden rastgele bir örnek toplayabilir , örnek ortalamasını ve örnek standart sapmasını bulabilir ve ortalama yüksekliğin gerçekte 15 inç olup olmadığını belirlemek için bir t-testi yapabiliriz.

Testin sıfır ve alternatif hipotezleri aşağıdaki gibidir:

H ₀ : u = 15

_Ha : µ ≠ 15

Test istatistiğinin formülü şu şekildedir:

t = ( X -μ) / (s/ √n )

burada x numune ortalamasıdır, μ varsayımsal ortalamadır (örneğimizde 15 olacaktır), s numune standart sapmasıdır ve n numune boyutudur.

T’nin değerini öğrendikten sonra karşılık gelen p değerini bulmak için istatistiksel yazılımı veya çevrimiçi hesap makinesini kullanabiliriz. P değeri belirli bir alfa seviyesinin altındaysa (ortak seçenekler 0,01, 0,05 ve 0,10’dur), o zaman boş hipotezi reddedebilir ve ortalama bitki boyunun 15 inçte eşit olmadığı sonucuna varabiliriz.

Bununla birlikte, bir t-dağılım tablosu kullanarak test p-değerini manuel olarak tahmin etmek de mümkündür . Bu yazımızda bunun nasıl yapılacağını açıklayacağız.

Örnek: Bir t-testinden p-değerinin manuel olarak hesaplanması

Sorun : Bob, belirli bir bitki türünün ortalama boyunun 15 inç olup olmadığını bilmek istiyor. Bunu test etmek için 20 bitkiden rastgele bir örnek topluyor ve örnek ortalamasının 14 inç ve örnek standart sapmasının 3 inç olduğunu buluyor. Gerçek ortalama popülasyon yüksekliğinin gerçekte 15 inç olup olmadığını belirlemek için 0,05 alfa düzeyini kullanarak bir t testi yapın.

Çözüm:

Adım 1: Boş ve alternatif hipotezleri belirtin.

H ₀ : u = 15

_Ha : µ ≠ 15

Adım 2: Test istatistiğini bulun.

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1,49

Adım 3: Test istatistiği için p değerini bulun.

P-değerini manuel olarak bulmak için n-1 serbestlik derecesine sahip t-dağılım tablosunu kullanmamız gerekir. Örneğimizde örneklem büyüklüğümüz n = 20, dolayısıyla n-1 = 19’dur.

Aşağıdaki t-dağılımı tablosunda sol taraftaki “19”a karşılık gelen satıra bakıp test istatistiğimizin mutlak değeri olan 1,49’u bulmaya çalışmamız gerekiyor.

Tabloda 1,49’un görünmediğini ancak 1,328 ve 1,729 değerleri arasında yer aldığını unutmayın.

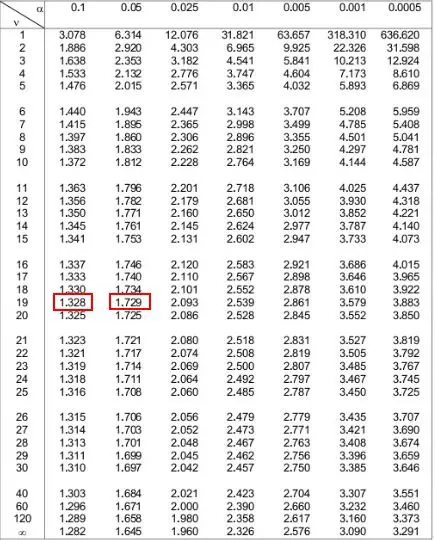
Daha sonra tablonun üst kısmında bu iki sayıya karşılık gelen iki alfa düzeyine bakabiliriz. Bunların 0.1 ve 0.05 olduğunu görüyoruz.

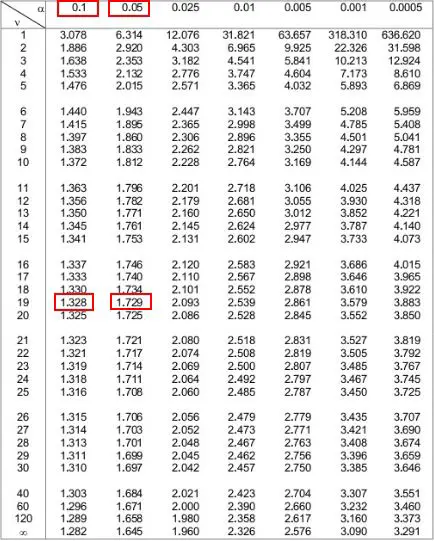
Bu, tek kuyruklu bir test için p değerinin 0,1 ile 0,05 arasında olduğu anlamına gelir. Buna 0,075 diyelim. T testimiz iki kuyruklu olduğundan bu değeri 2 ile çarpmamız gerekiyor. Yani tahmini p değerimiz 0,075 * 2 = 0,15 olacaktır.

Adım 4: Bir sonuç çıkarın.

Bu p değeri seçilen alfa seviyesi olan 0,05’ten düşük olmadığından sıfır hipotezini reddedemeyiz. Bu nedenle, bu bitki türünün gerçek ortalama boyunun 15 inçten başka bir şey olduğunu söyleyecek yeterli kanıtımız yok.

Sonuçları hesap makinesiyle kontrol edin

Tahmini p-değerimizin gerçek p-değerine ne kadar yakın olduğunu görmek için t -testi istatistiğimizi ve serbestlik derecemizi çevrimiçi bir p-değeri hesaplayıcısına bağlayabiliriz:

Gerçek p değeri 0,15264’tür ve bu bizim tahmini p değerimiz olan 0,15’e oldukça yakındır.

Çözüm

Bu makalede, t-dağılımı tablosunu kullanarak bir t-testinin p-değerini manuel olarak tahmin etmenin mümkün olduğunu gördük. Ancak çoğu senaryoda p-değerini hiçbir zaman elle hesaplamak zorunda kalmayacaksınız ve testin tam p-değerini bulmak için R ve Excel gibi istatistiksel yazılımları veya çevrimiçi hesap makinesini kullanabilirsiniz.

Çoğu durumda, özellikle de sıkı istatistiksel çalışmalarda ve deneylerde, mümkün olduğunca kesin olması için bir t-testinden tam p-değerini bulmak için bir hesap makinesi kullanmak isteyeceksiniz, ancak her zaman manuel olarak tahmin edebileceğinizi bilmek güzel. Kesinlikle ihtiyacınız varsa t testinden elde edilen p değeri.