Excel'de çeyrekler arası aralık (iqr) nasıl hesaplanır?
Bu eğitimde, Excel’de bir veri kümesinin çeyrekler arası aralığının nasıl hesaplanacağı açıklanmaktadır.
Çeyrekler arası aralık nedir?
Genellikle IQR olarak adlandırılan çeyrekler arası aralık , bir veri kümesinin ortadaki %50’lik kısmının dağılımını ölçmenin bir yoludur. Bir veri setinin ilk çeyreği* (Q1) ile üçüncü çeyreği (Q3) arasındaki fark olarak hesaplanır.
*Çeyrekler basitçe bir veri kümesini dört eşit parçaya bölen değerlerdir.
Örneğin aşağıdaki veri setine sahip olduğumuzu varsayalım:
[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]
Üçüncü çeyrek 91 , ilk çeyrek ise 75,5 çıkıyor. Yani bu veri seti için çeyrekler arası aralık (IQR) 91 – 75,5 = 15’tir . Bu bize bu veri kümesindeki değerlerin ortadaki %50’sinin dağılımını anlatır.
Excel’de Çeyrekler Arası Aralık Nasıl Hesaplanır?
Microsoft Excel’in bir veri kümesinin IQR’sini hesaplamak için yerleşik bir işlevi yoktur, ancak aşağıdaki bağımsız değişkenleri alan QUARTILE() işlevini kullanarak bunu kolayca bulabiliriz:
DÖRTTEBİRLİK(dizi; çeyrek)
- dizi: ilgilendiğiniz veri dizisi.
- quart: hesaplamak istediğiniz çeyrek.
Örnek: Excel’de IQR’yi arama
Aşağıdaki veri seti için IQR’yi bulmak istediğimizi varsayalım:
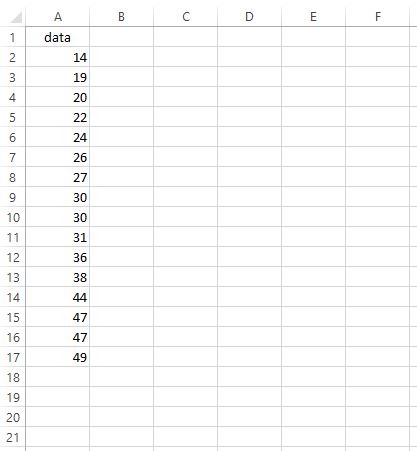
IQR’yi bulmak için aşağıdaki adımları uygulayabiliriz:
Adım 1: Q1’i arayın .
İlk çeyreği bulmak için istediğimiz herhangi bir hücreye =QUARTILE(A2:A17, 1) yazmamız yeterlidir:
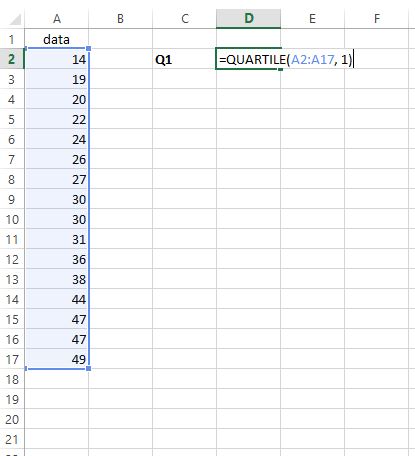
Adım 2: Q3’ü arayın .
Üçüncü çeyreği bulmak için istediğimiz herhangi bir hücreye =QUARTILE(A2:A17, 3) yazıyoruz:
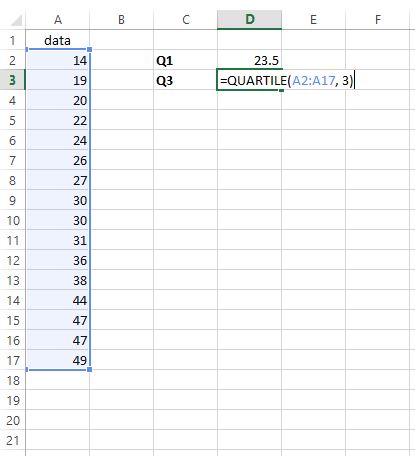
Adım 3: IQR’yi bulun .
Çeyrekler arası aralığı (IQR) bulmak için Q1’i Q3’ten çıkarmamız yeterlidir:
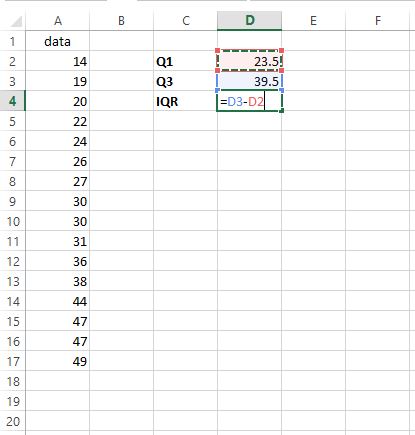
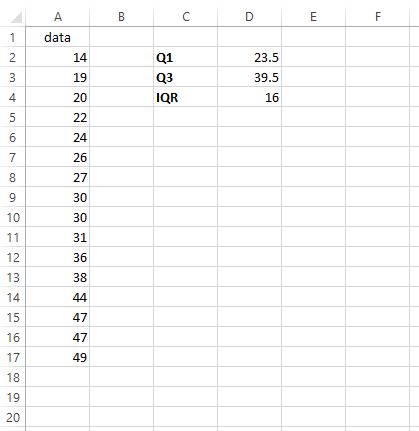
IQR’nin 39,5 – 23,5 = 16 olduğu ortaya çıkıyor. Bu bize, bu özel veri setinde değerlerin ortadaki %50’sinin nasıl dağıldığını anlatır.
Daha kısa bir yaklaşım
Önceki örnekte veri kümesinin çeyrekler arası aralığını bir formül kullanarak da bulabileceğimizi unutmayın:
=DÖRTTEBİR(A2:A17, 3) – DÖRTTEBİR(A2:A17, 1)
Bu aynı zamanda 16 değerini de verecektir.
Çözüm
Çeyrekler arası aralık, bir veri kümesinin “yayılmasını” ölçmenin yalnızca bir yoludur. Yayılımı ölçmenin diğer yolları aralık, standart sapma ve varyanstır.
Yayılımı ölçmek için IQR kullanmanın avantajı aykırı değerlere karşı dayanıklı olmasıdır . Bize yalnızca veri kümesinin ortadaki %50’lik kısmının dağılımını söylediği için alışılmadık derecede küçük veya alışılmadık derecede büyük aykırı değerlerden etkilenmez.
Bu, bize bir veri kümesindeki en büyük ve en küçük değerler arasındaki farkı söyleyen metrik benzeri bir aralığa kıyasla dağılımı ölçmenin tercih edilen bir yolu olmasını sağlar.