Excel'de tahmin aralığı nasıl oluşturulur

İstatistikte basit doğrusal regresyon , tahmin değişkeni x ile yanıt değişkeni y arasındaki ilişkiyi ölçmek için kullanabileceğimiz bir tekniktir.

Basit bir doğrusal regresyon uyguladığımızda, x ile y arasındaki ilişkiyi tanımlayan ve şu şekilde yazılabilen bir “en iyi uyum çizgisi” elde ederiz:

ŷ = b ₀ + b ₁ x

Altın:

• ŷ yanıt değişkeninin tahmin edilen değeridir
• b ₀ y kesme noktasıdır
• b ₁ regresyon katsayısıdır
• x, tahmin değişkeninin değeridir

Bazen belirli bir x ₀ değeri için bir tahmin aralığı oluşturmak için bu en iyi uyum çizgisini kullanmak isteriz; bu, tahmin edilen değer ŷ ₀ civarında bir aralıktır, öyle ki popülasyondaki y’nin gerçek değerinin %95 olma ihtimali vardır. x _0’a karşılık gelen değer bu aralığa dahildir.

Belirli bir x ₀ değeri için tahmin aralığını hesaplama formülü yazılmıştır:

ŷ ₀ +/- t _α/2,df=n-2 * se

Altın:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

Formül biraz korkutucu görünebilir ancak Excel’de hesaplanması aslında basittir. Daha sonra, Excel’de belirli bir değere ilişkin tahmin aralığını hesaplamak için bu formülü kullanmanın bir örneğini göreceğiz.

Örnek: Excel’de Tahmin Aralığı Nasıl Oluşturulur

Aşağıdaki veri seti, 15 farklı öğrencinin aldığı sınav puanının yanı sıra çalışılan saat sayısını da göstermektedir:

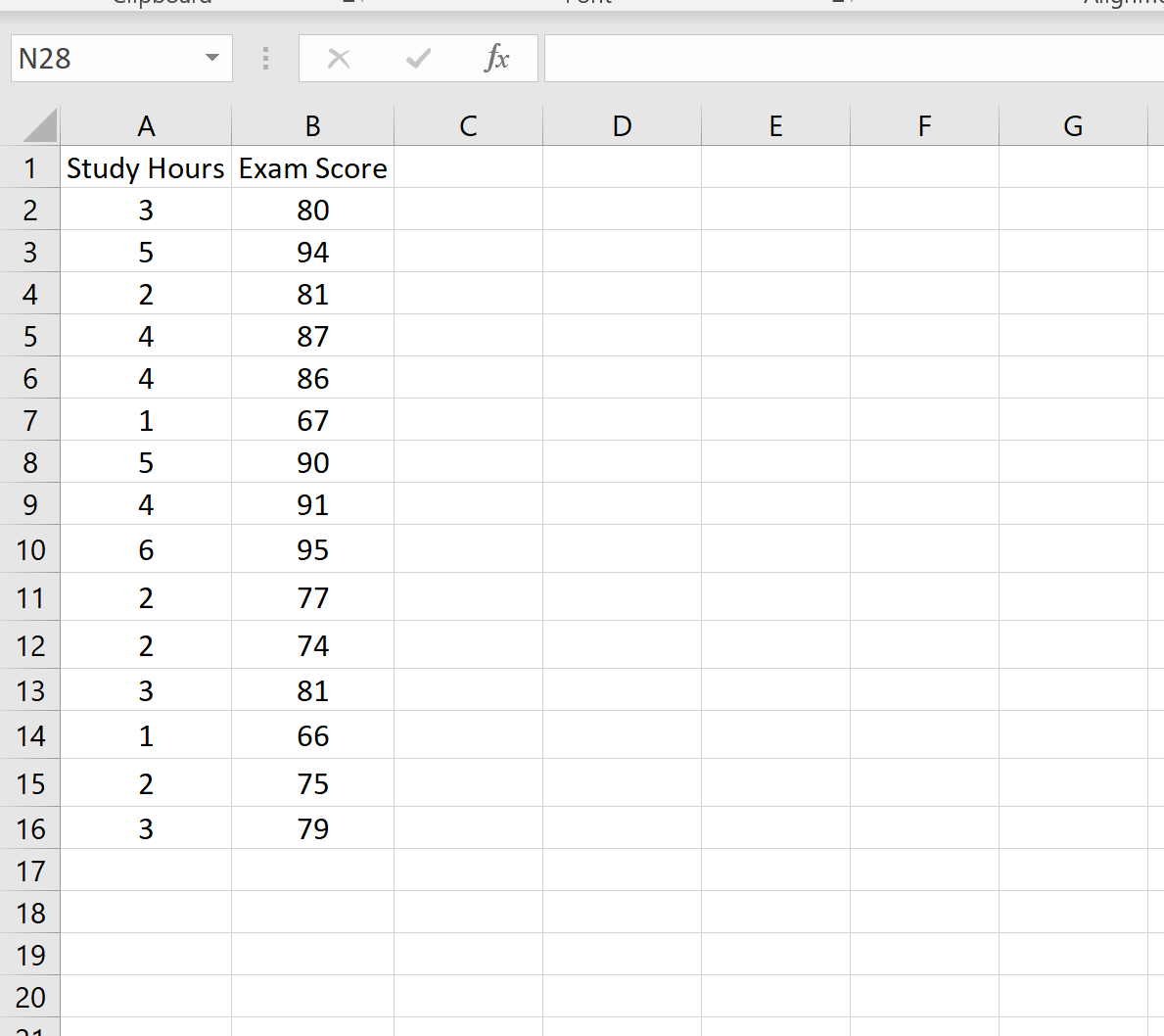
Diyelim ki x ₀ = 3 değeri için %95’lik bir tahmin aralığı oluşturmak istiyoruz. Yani, sınava giren bir öğrencinin sınav puanının bu aralığa düşme olasılığı %95 olacak şekilde bir aralık oluşturmak istiyoruz. 3 saat.

Aşağıdaki ekran görüntüsü, bu tahmin aralığını elde etmek için gereken tüm değerlerin nasıl hesaplanacağını göstermektedir.

Not: F sütunundaki formüller, E sütunundaki değerlerin nasıl hesaplandığını gösterir.

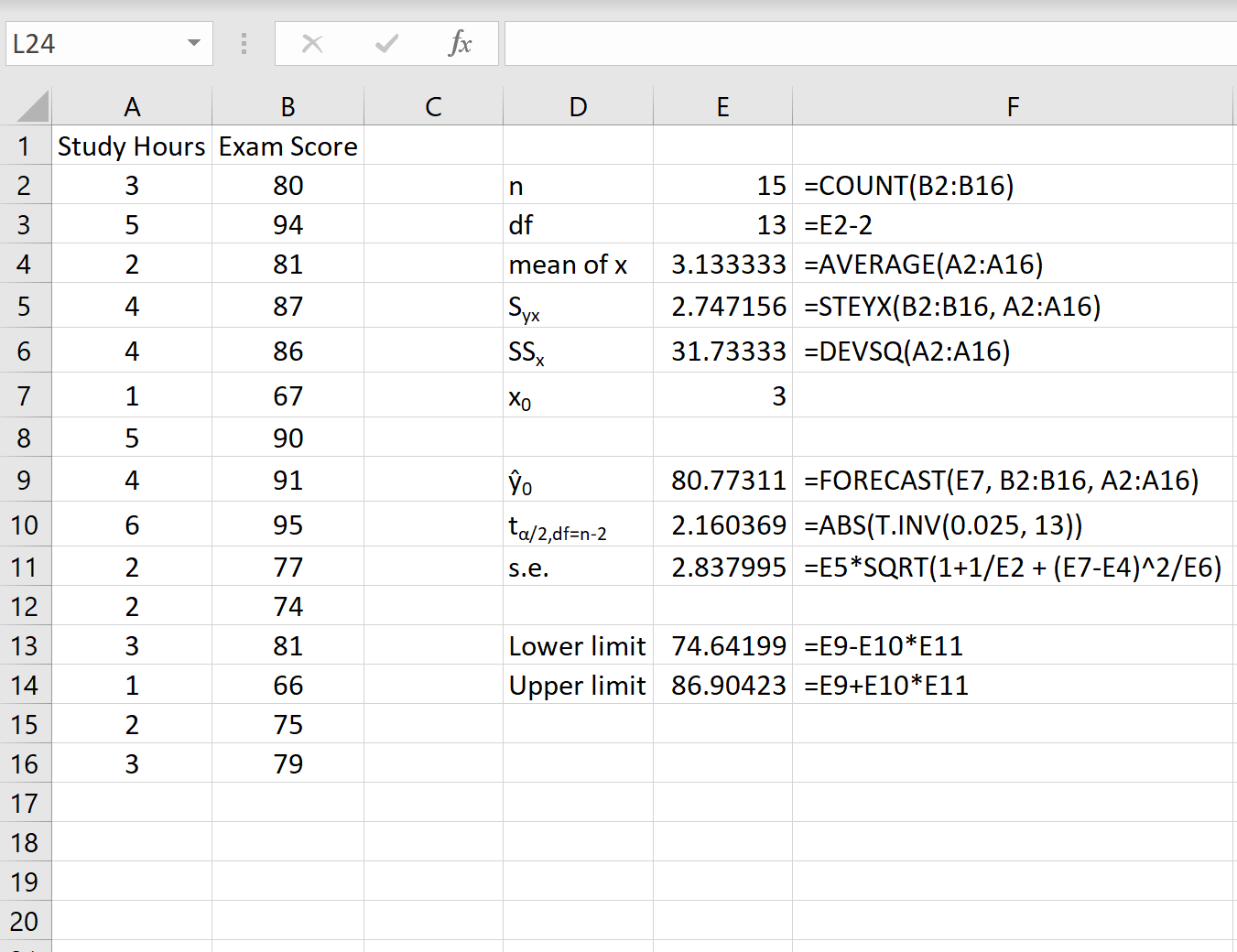
x ₀ = 3 değeri için %95 tahmin aralığı (74,64, 86,90)’ dir. Yani 3 saat ders çalışan bir öğrencinin 74,64 ile 86,90 arasında puan alacağını %95 olasılıkla öngörüyoruz.

Kullanılan hesaplamalara ilişkin bazı notlar:

• t _{α/2,df=n-2’nin} t-kritik değerini hesaplamak için %95’lik bir tahmin aralığı istediğimizden α/2 = 0,05/2 = 0,25 kullandık. Daha yüksek tahmin aralıklarının (örneğin, %99 tahmin aralığı) daha geniş aralıklara yol açacağını unutmayın. Tersine, daha küçük bir tahmin aralığı (örneğin, %90’lık bir tahmin aralığı) daha dar bir aralığa yol açacaktır.
• ŷ ₀ için tahmin edilen değeri elde etmek için =FORECAST() formülünü kullandık ancak =FORECAST.LINEAR() formülü tam olarak aynı değeri döndürecektir.